1. The document contains an unsolved mathematics paper from 1985 containing multiple choice, multiple answer, true/false, and fill in the blank questions. 2. The questions cover topics like complex numbers, vectors, geometry, functions, and series. 3. Answers to the questions are not provided, but the document directs readers to a website for solutions.

1. IIT JEE –Past papersMATHEMATICS- UNSOLVED PAPER - 1985

2. SECTION – ISingle Correct Answer TypeThere are five parts in this question. Four choices are given for each part and one of them is correct. Indicate your choice of the correct answer for each part in your answer-book by writing one of the letters (a), (b), (c) or (d) whichever is appropriate.

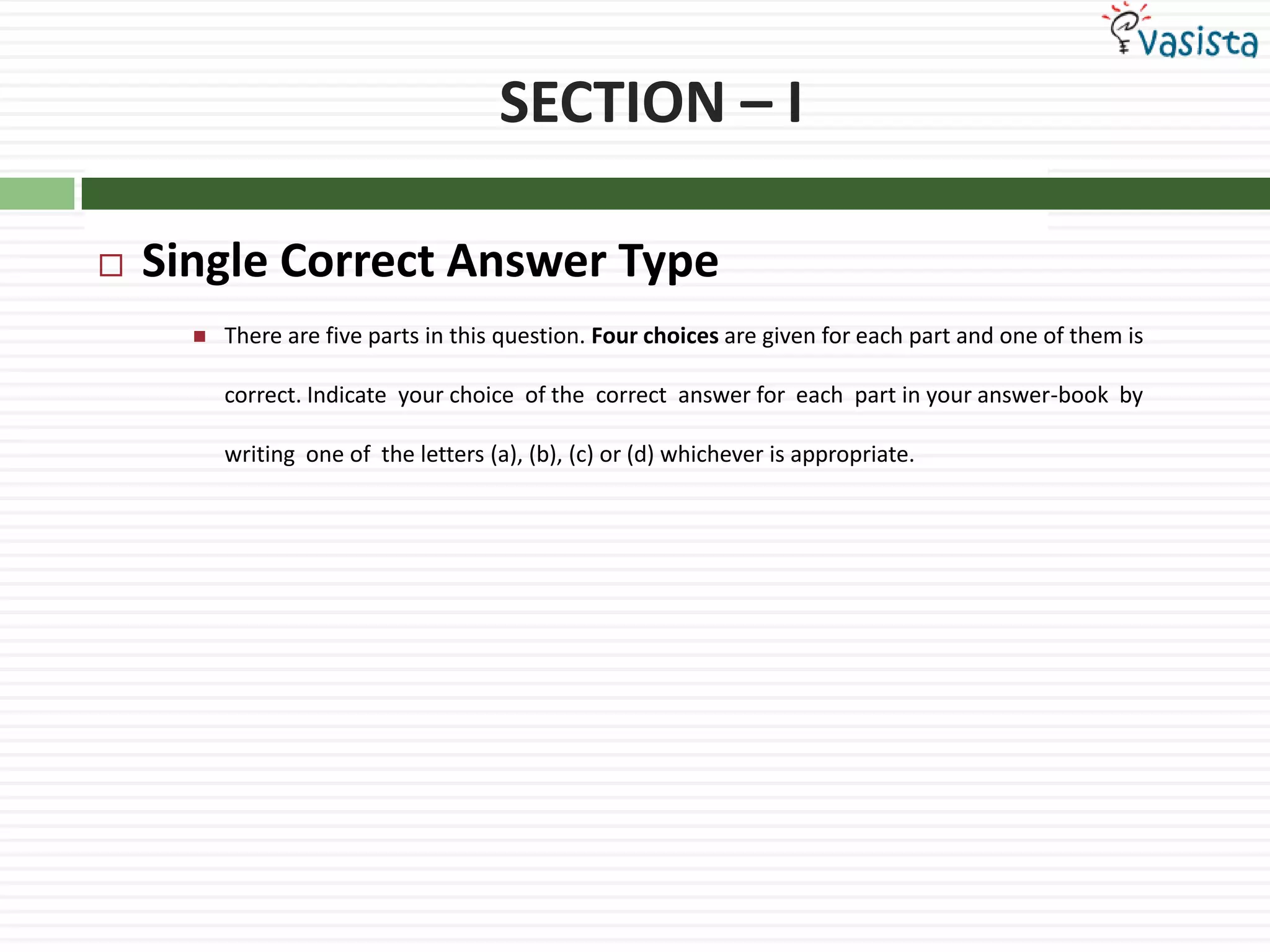
3. 01ProblemIf = 0, [x] = 0Where [x] denotes the greatest integer less then or equal to x, then equals:10-1None of these

4. Problem02If a, b, c is in GP, then the equations have a common root if are in: APGPHPNone of these

5. Problem03 For any integer n, integralπ10None of these

6. Problem04If a, b, c and u, v, w are complex numbers representing the vertices of two triangles such that where r is a complex number, then the two triangles:Have the same areaAre similarAre congruentNone of these

7. Problem05If then x lies in the interval:( 2 ∞ )(1, 2)(-2, -1)None of these

8. SECTION – IIMultiple Correct Answer Type There are there parts in this question. Each part has one or more than one correct answer. Indicate all correct answers for each part by writing the corresponding letters from (a), (b), (c) or (d) in the answer-book.

9. 01ProblemThere lines are concurrent if:a. b.c. d. None of these

10. Problem02If then Is continuous but not differentiable at x = 0 Is differentiable at x = 0 Is not differentiable at x =0None of these

11. Problem03If are complex numbers such that then the pair of complex numbers satisfies:|w1| = 1|w2| = 1Re None of these

12. SECTION – IIIEach of which either True or FalseThis question contains five statements, each of which is either true of false. Indicate your choice of the answer in the answer-book by writing TRUE or FALSE for each statement.

13. 01ProblemIf then the triangles with vertices and must be congruent.

14. Problem02The product of any r consecutive natural numbers is always divisible by r!

15. Problem03If three complex numbers are in A.P. Then they lie on a circle in the complex plane.

16. Problem04If are p positive integers, whose sum is an even number, then the number of odd integers among them is odd

17. Problem05No tangent can be drawn from the point (5/2, 1) to the circumcircle of the triangle with vertices

18. Problem06If where then has at least two real roots.

19. SECTION – IVFill in the BlanksIn This question contains fourteen incomplete statements. Determine your answers to be inserted in the blanks so that the statements are complete. Write these answers only in your answer – book, strictly in the order in which the statement appear below::

20. 01ProblemIf (x), r = 1, 2, 3, are polynomials in x such that and then is ___________________.

21. Problem02If and the vectors A = are non-coplanar, then the product abc = ________________.

22. Problem03 If and only if the relation between P (A) and P (B) is ___________.

23. Problem04If A, B, C are three non-coplanar vectors, then: ___________.

24. Problem05Let A be a set of n idstinct elements. Then the total number of distinct functions from A to A is __________ and out of these __________ are onto functions.

25. Problem06The set of all real numbers a such that and are the sides of a triangle is ____________.

26. Problem07In a triangle ABC, if cot A cot B and cot C are in AP< then a2,b2,c2 are in __________ Progression

27. Problem08Let be a circle. A pair of tangents from the point (4, 5) with a pair of radii form a quadrilateral of area ____________.

28. Problem09If A= (1, 1 1), C = (0, 1, -1) are given vectors then a vector B satisfying the equations A x B = C and A B = 3 is ____________.

29. Problem10The orthocenter of the triangle formed by the lines lies in quadrant number. _______________

30. Problem11If then the domain of f(x) is _____________ and its range is ______________.

31. Problem12If is _______________.

32. Problem13A box contains 100 tickets numbered 1, 2,….., 100. Two tickets are Chosen at random. It is given that the maximum number on the two chosen tickets is not more than 10. The minimum number on them is 5 with probability_____________.

33. Problem14From the origin, chords are drawn to the circle the equation of the locus of the mid-points of these chords is ______________.

34. FOR SOLUTION VISIT WWW.VASISTA.NET