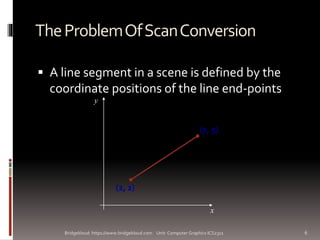
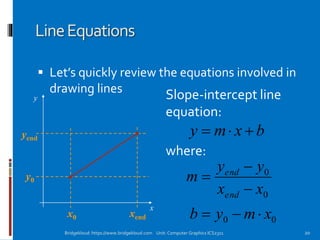
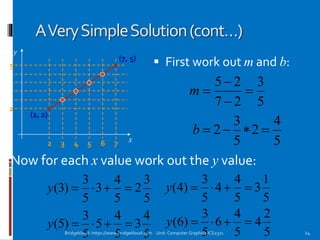
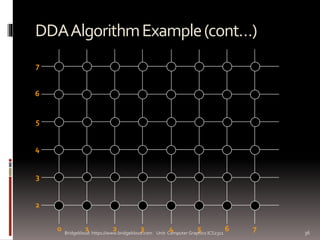
The document discusses various line drawing algorithms in computer graphics, emphasizing the importance of accurately rendering lines on pixel-based displays. It covers concepts such as rasterization, the challenges of aliasing, and details specific algorithms like DDA (Digital Differential Analyzer) and Bresenham's Algorithm. The document also highlights considerations for achieving visually appealing results while maintaining performance efficiency.

![ArchitectureOfAGraphicsSystem
[remember this?]
System Bus
CPU
Display
Processor
System
Memory
Display
Processor
Memory
Frame
Buffer
Video
Controller
MonitorMonitor
2Bridgekloud: https://www.bridgekloud.com Unit: Computer Graphics ICS2311](https://image.slidesharecdn.com/ics2311l03linedrawingalgorithms-200819165551/85/line-drawing-algorithms-COMPUTER-GRAPHICS-Graphical-Programming-2-320.jpg)