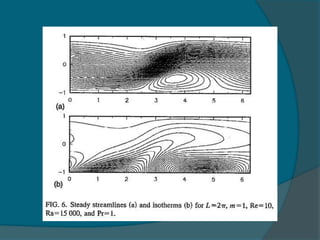
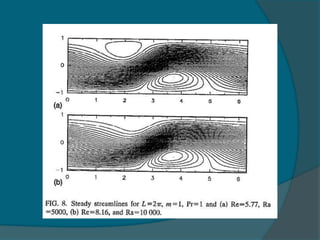
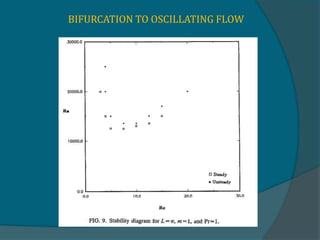
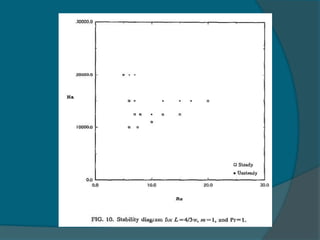
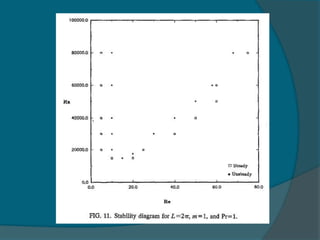
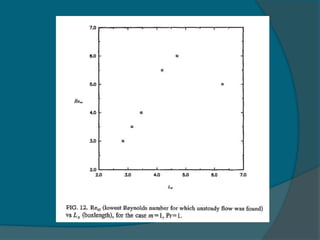
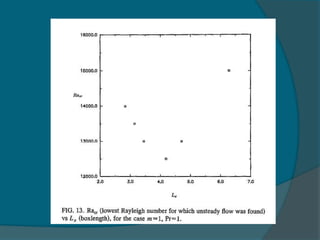
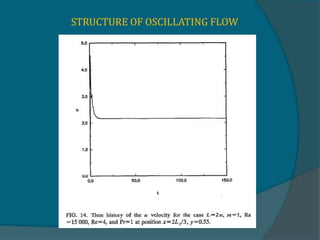
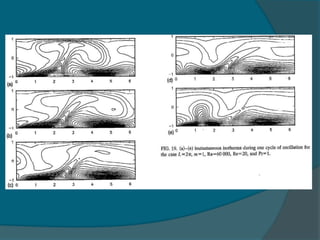
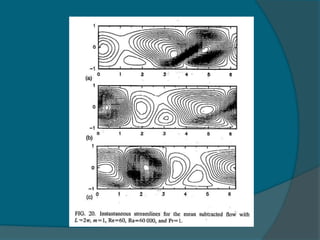
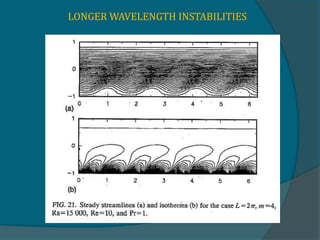
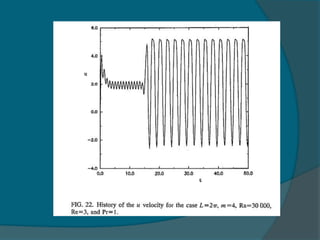
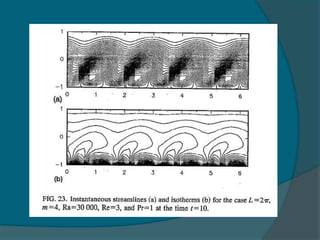
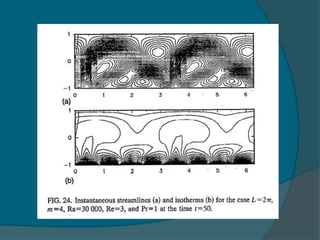
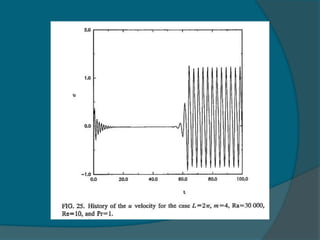
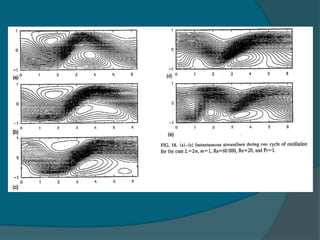
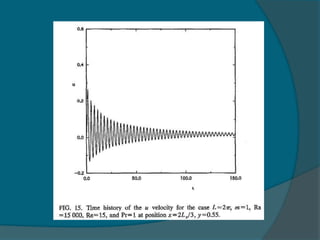
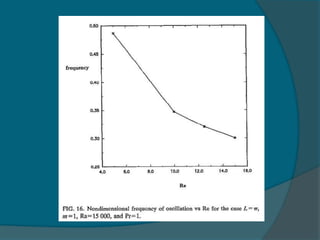
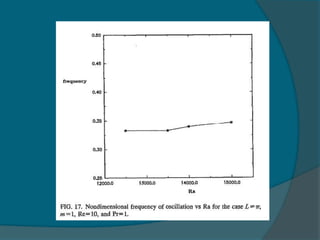
Two-dimensional numerical simulations were conducted of flow through a channel with spatially periodic temperature boundary conditions on the lower wall. The simulations showed: 1) A bifurcation to oscillatory flow occurs at Reynolds numbers as low as 4 and Rayleigh numbers as low as 14,500. 2) The frequency of oscillation decreases with increasing Reynolds number and is independent of the Rayleigh number. 3) Maps were created showing different flow regimes for varying periodicities of the temperature boundary conditions.

1. BY
Sara Q. Zhang (NASA)
Andrew Tangborn (University of Maryland, Baltimore County)
PRESENTED BY
Muhammad Ilyas
SP16-PMT-003
COMSATS Institute of
Information Technology,
Islamabad

2. ABSTRACT
Two-dimensional numerical simulations of flow through a channel with spatially
periodic temperature boundary conditions at the lower wall have been carried out.
A spectral method with a Fourier series expansion in the streamwise direction and a
Chebyshev expansion in the vertical direction is employed.
A bifurcation to a limit cycle occurs at Reynolds numbers as low as Re=4 and Rayleigh
numbers as low as Ra= 14 500.
The frequency of oscillation decreases with Re and is essentially independent of Ra.
Maps of flow regimes for varying periodicities have been created.

3. KEYWORDS AND TERMINOLIGIES
CONVECTION
Convection is the mode of energy transfer between a solid surface and the
adjacent liquid or gas that is in motion, and it involves the combined effects of
conduction and fluid motion. The faster the fluid motion, the greater the convection
heat transfer. In the absence of any bulk fluid motion, heat transfer between a solid
surface and the adjacent fluid is by pure conduction.
NATURAL CONVECTION
Natural convection is a mechanism, or type of heat transport, in which the fluid
motion is not generated by any external source (like a pump, fan, suction device,
etc.) but only by density differences in the fluid occurring due to temperature
Gradient. The driving force for natural convection is buoyancy, a result of
differences in fluid density.
FORCED CONVECTION
Forced convection is a mechanism, or type of transport in which fluid motion is
generated by an external source (like a pump, fan, suction device, etc.). It should be
considered as one of the main methods of useful heat transfer as significant
amounts of heat energy can be transported very efficiently. This mechanism is
found very commonly in everyday life, including central heating, air
conditioning, steam turbines, and in many other machines.

4. MIXED CONVECTION
Mixed convection, occurs when natural convection and forced convection mechanisms
act together to transfer heat. This is also defined as situations where both pressure
forces and buoyant forces interact.
REYNOLDS NUMBER
In fluid mechanics, the Reynolds number (Re) is a dimensionless quantity that is
defined as the ratio of inertial forces to viscous forces.
• Laminar flow occurs at low Reynolds numbers, where viscous forces are dominant, and
is characterized by smooth, constant fluid motion.
• Turbulent flow occurs at high Reynolds numbers and is dominated by inertial forces,
which tend to produce chaotic eddies, vortices and other flow instabilities.
RAYLEIGH NUMBER
The Rayleigh number (Ra) is named after Lord Rayleigh and is defined as the product of
the Grashof number, which describes the relationship between buoyancy and
viscosity within a fluid, and the Prandtl number, which describes the relationship
between momentum diffusivity and thermal diffusivity. Hence the Rayleigh number
itself may also be viewed as the ratio of buoyancy and viscosity forces multiplied by the
ratio of momentum and thermal diffusivities.

5. THERMAL DIFFUSIVITY
Thermal diffusivity of a material can be viewed as the ratio of the heat conducted
through the material to the heat stored per unit volume.
BIFURCATION
Bifurcation means the splitting of a main body into two parts.
LIMIT CYCLE
A limit cycle is an isolated closed trajectory; this means that its neighboring trajectories
are not closed – they spiral either towards or away from the limit cycle.
ISOTHERM
A curve on a diagram joining points representing states of equal temperature.

6. TOLLMIEN-SCHLICHTING WAVE
In fluid dynamics, a Tollmien–Schlichting wave (often abbreviated T-S wave) is a
streamwise instability which arises in a viscous boundary layer.
HELMHOLTZ INSTABILITY
Helmholtz type of instability is the instability in which the TS wave has been excited by the
groove.
FLUX
In transport phenomena (heat transfer, mass transfer and fluid dynamics), flux is defined as
the rate of flow of a property per unit area.
BOUSSINESQ APPROXIMATION
In fluid dynamics, the Boussinesq approximation named for Joseph Valentin Boussinesq,
is used in the field of buoyancy-driven flow (also known as natural convection). It ignores
density differences except where they appear in terms multiplied by g, the acceleration due
to gravity.

7. INTRODUCTION
The destabilization of low speed channel flows has attracted attention recently. There
has been particular interest in the structures of the resulting unsteady flows and the
mechanism by which the instability occurs. Applications of these instabilities include
the cooling of electronic equipment and computer circuits [1]. Recent work has
emphasized the prediction and analysis of the frequency behavior of unstable flows.
One particularly successful means of destabilizing a channel flow is the placement of a
groove along one of the walls, perpendicular to the direction of flow. Ghaddar et al. [2],
[3] carried out numerical simulations of a two-dimensional grooved channel flow. They
found that the flow begins to oscillate at a critical Reynolds number of Re=975 for the
geometry studied.

8. Cheng et al.[4] carried out numerical calculations on steady mixed convection in the
entry region of a rectangular duct with a uniform wall flux on all sides. The buoyancy
was found to shorten the entry region, due to the secondary motion carrying hot fluid
away from the walls.
Ostrach and Kamotani [5] carried out experiments on mixed convection with uniform
heating on the lower surface. It was observed that for Ra<8000 and l0<Re<100 steady
vortex rolls aligned to the flow direction are the dominant structure. For Ra>8000 this
structure was found to be unstable and an unsteady and irregular flow appeared.

9. Natural convection in a fluid layer uniformly heated from below will generally be three
dimensional. Busse and Clever[6] investigated the transition from two to three-
dimensional convection over a range of Prandtl numbers 0.01 to 100. They showed
that, for a wave number of , and Prandtl numbers close to 1, two-dimensional
convection can only exist over a very small range of Rayleigh numbers.
Kennedy and Zebib[7] carried out two-dimensional steady numerical calculations of
mixed convection with localized heating on the lower and upper surfaces. The resulting
flow separates just downstream of the heat source so that the vortex roll is now cross
stream and it can be expected that this flow to become unstable with sufficiently larger
driving forces.
3.14
 

10. Unsteady two-dimensional numerical simulations of mixed convection with spatially
periodic heating have been carried out by Wang et al.[8] and Tangborn[9]. Wang et al.
found a region in (Re, Ra) space where the flow is unsteady and extends as low as
Re=2.0. Tangborn showed that if the upper wall is insulated, the flow is stabilized and
will not become unsteady unless the Reynolds number is raised to Re=100. These
results show that this flow becomes unsteady when there is a balance between
buoyancy and pressure forces.

11. MOTIVATION
• Part of the motivation for this work was that the separation will occur in the channel
and will not be trapped in a groove. The separation vortex can then be carried down
stream by the pressure-driven flow, thereby creating an unsteady flow.
• This paper is concerned with the nature of this instability, its dependence on geometry
and the wave structure of the flow. Then these results will be used to learn whether this
instability is similar to the well-studied inviscid shear instability, the grooved channel
flow, or whether this is an entirely different mechanism that leads to a wholly unrelated
path to turbulence.

12. PROBLEM FORMULATION
In this work two-dimensional flow between parallel plates is considered. Constant fluid
properties and the Boussinesq approximation are assumed. The flow is assumed periodic
in the streamwise (x) direction with periodicity Lx . The vertical distance between the
parallel plates is 2.0 (- 1<y < 1). Zero velocity is imposed at the two horizontal surfaces.
Tangborn showed that an insulated upper surface will create a stably stratified flow in
the upper half channel that will not begin to oscillate until relatively high Re and Ra
values are reached. Therefore, the uniform temperature Tu is imposed at the upper
surface while a spatially periodic boundary condition is imposed at the lower wall that
has the form , where m=l, 2, 3, etc. Initial conditions are zero temperature
and velocity every where in the domain.
 
2
sin mx L


13. GEOMETRY OF THE PROBLEM

14. GOVERNING EQUATIONS
The non-dimensional governing equations are
 
 
 
2
2
2
1 Ra ˆ, (1)
Re Pr Re
1
(2)
RePr
With boundary conditions
0 1, 3
0 1, 4
sin 2 1 (5)
V
V V p V j
t
V
t
V at y
at y
mx L at y


 

 

      


   

  
 
  

15. where the lengths have been non-dimensionalized with respect to the channel half-
height, h = 1, and velocity with respect to the characteristic velocity of the forced
convection ; is defined as the maximum velocity that would occur in the
absence of natural convection (i.e., plane-Poiseuille flow).
The Reynolds number is defined by and
the Rayleigh number is defined by
is the thermal expansion coefficient, g is the acceleration due to gravity, is the
diffusivity, and is the kinematic viscosity.
U U
U
Re ,
h


 
3
max
8
Re u
gh T T




 


16. NUMERICAL METHOD
The numerical procedure employed here is essentially the same as the technique
used by Kim et al [13]. The curl of the momentum equations is taken so as to remove
pressure as a boundary condition.
A coupled system of three (including the energy equation) second-order equations
is expanded by Fourier series in x and is solved by the Chebyshev-tau method.
Time stepping is Crank-Nicolson for the viscous (linear) terms and Adams-Bashforth
for the convective (nonlinear) terms.
The 32X32 (x and y directions), two-dimensional mesh is used for most of the
simulations.

17. NATURAL CONVECTION-RESPONSE TO THREE-
DIMENSIONAL DISTURBANCES

19. TWO-DIMENSIONAL STEADY MIXED CONVECTION

23. BIFURCATION TO OSCILLATING FLOW

28. STRUCTURE OF OSCILLATING FLOW

35. LONGER WAVELENGTH INSTABILITIES

40. CONCLUSION
 Direct numerical simulations of steady and unsteady two-dimensional channel
flows with spatially periodic heating were carried out using 32X32 mesh points.
 Both of these flows appear to be destabilized by the existence of a separation
region.
 The mixed convection flow shows a stronger oscillatory motion in the absence of
external forcing due to the fact that the vortex is not being held in place by a
groove.
 The bifurcation to a limit cycle in both of these flows indicates that they each follow
a stepwise path to turbulence rather than a sudden transition. The first step in the
grooved channel occurs a Recr=575 and the first step in this mixed convection
occurs at Recr=2 (for L x =2pi and m=l).
 The critical Rayleigh number can be reduced by shortening the periodicity of
the thermal boundary conditions.

41. REFERENCES