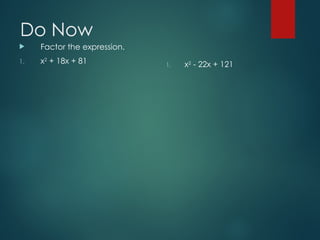
The document explains how to solve quadratic equations by completing the square, detailing the steps to find the necessary value of 'c' to form perfect square trinomials. It provides examples of factoring expressions and solving equations, including specific expressions to practice with. The approach includes determining half of the 'b' coefficient, squaring it, and replacing 'c' in the equation.

1. Do Now
 Factor the expression.
1. x2
+ 18x + 81 1. x2
- 22x + 121

2. Completing the
Square
OBJECTIVE:
SOLVE QUADRATIC EQUATIONS BY COMPLETING THE
SQUARE

3. Completing the Square
 Find the value of c that makes x2
- 6x + c a
perfect square trinomial. Then write the
expression as the square of a binomial.
 To find the value of c, use the “b” value
(ax2
+bx+c):
1. Find half the coefficient of x.
2. Square the result of Step 1.
3. Replace c with the result of Step 2.
 Answer:
when
when c
c = 9,
= 9, x
x2
2
– 6
– 6x
x + 9 = (
+ 9 = (x
x – 3)
– 3)2
2
x
x2
2
– 6
– 6x
x + 9
+ 9
(– 3)
(– 3)2
2
=
=
½ (– 6)
½ (– 6) =
=

4. Example: Completing the Square
 Find the value of c that makes x2
- 12x + c a
perfect square trinomial. Then write the
expression as the square of a binomial.
 To find the value of c, use the “b” value
(ax2
+bx+c):
1. Find half the coefficient of x.
2. Square the result of Step 1.
3. Replace c with the result of Step 2.
 Answer:

5. Practice
Find the value of c that makes the expression a
perfect square trinomial. Then write the
expression as the square of a binomial.
3. x2
- 10x + c
4. x2
+ 18x + c

6. Solving Quadratics

7. Example

8. Solve the equation by
completing the square.
1. x2
+ 2x – 3 = 0
2. x2
- 6x + 16 = 0

9. Solve the equation by
completing the square.
3. x2
- 8x - 20 = 0
4. x2
+ 4x - 15 = 21

10. Solve the equation by
completing the square.
5. x2
- 2x - 2 = 0
6. x2
+ 6x + 3 = 0