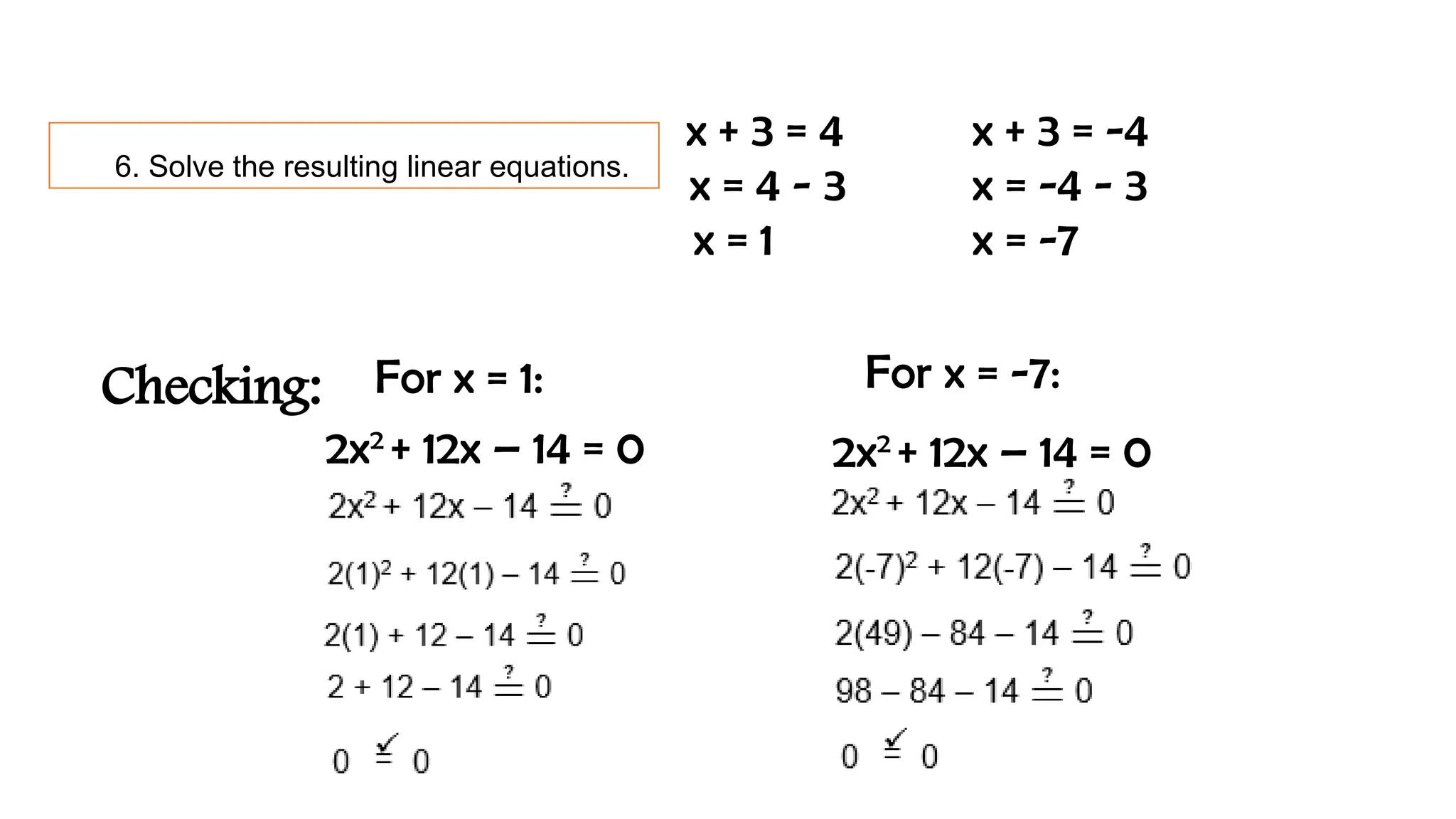The document outlines the method of solving quadratic equations by completing the square, detailing a series of steps to transform the equation into a solvable form. Specific examples illustrate how to apply the method and check solutions to ensure they satisfy the original equation. It emphasizes the importance of achieving a positive value for k to obtain real number solutions.

1. Solving Quadratic
Equations by Completing
the Square
by: Teacher Novie
Quarter 1 – Week 2 (Lesson 3)
MELC Based
GRADE 9
MATHEMATICS

2. LEARNING OBJECTIVE:
1. Solve quadratic equations by completing
the square.

3. Perfect Square trinomial
x2
+ 2x + 1
Square of Binomial
(x + 1)²
x2
+ 20x + 100 (x + 10)²
x2
+ 6x + 9 (x + 3)²

4. Another method of solving quadratic equations is by
completing the square. This method involves
transforming the quadratic equation ax2
+ bx + c = 0. into
the form (x – h)2
= k, where k ≥ 0. The value of k should
be positive to obtain a real number solution.

5. 1. Divide both sides of the equation by a then simplify.
2. Write the equation such that the terms with variables are on the left side
of the equation and the constant term is on the right side.
3. Add the square of one-half of the coefficient of x on both sides of the
resulting equation. The left side of the equation becomes a perfect square
trinomial.
4. Express the perfect square trinomial on the left side of the equation as a
square of a binomial.
5. Solve the resulting quadratic equation by extracting the square root.
6. Solve the resulting linear equations.
7. Check the solutions obtained against the original equation.
To solve the quadratic equation ax2
+ bx + c = 0 by completing
the square, the following steps can be followed:

6. Example #1. Find the solutions of 2x2
+ 12x – 14 = 0 by
completing the square.
Solution:
2x2
+ 12x – 14 = 0
1. Divide both sides of the
equation by the coefficient
a then simplify.
2. Rewrite the equation
x2
+ 6x = 7
x2
+ 6x + 9 = 7 + 9
x2
+ 6x + 9 = 16
(x + 3)2
= 16
4. Express the perfect square
trinomial on the left side of the
equation as a square of a
binomial.
5. Solve the resulting quadratic
equation by extracting the square
x2
+ 6x - 7= 0

7. 6. Solve the resulting linear equations.
x + 3 = 4 x + 3 = -4
x = 4 - 3
x = 1
x = -4 - 3
x = -7
Checking:
2x2
+ 12x – 14 = 0
For x = 1: For x = -7:
2x2
+ 12x – 14 = 0

8. Example #2. Find the solutions of x2
- 8x - 9 = 0.
Solution:
x2
- 8x - 9 = 0 x2
- 8x = 9
x2
- 8x + 16 = 9 + 16
x2
- 8x + 16 = 25
(x - 4)2
= 25

9. Checking:
For x = 9: For x = -1:

10. Example #3. Find the solutions of x2
– 2x = 7 by completing
the square.
Solution: x2
– 2x = 7
½(b)= 1/2(2) = 1² = 1 x2
– 2x + 1 = 7 + 1
x2
– 2x + 1 = 8
(x – 1)2
= 8
x – 1 =
x – 1 =
x – 1 =

11. Continuation….
x – 1 = x – 1 = -
x = x =