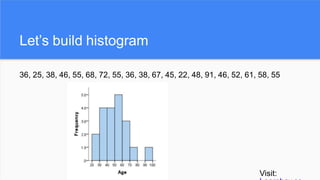
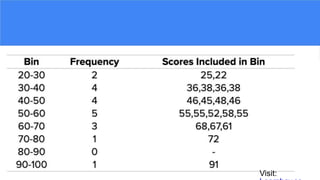
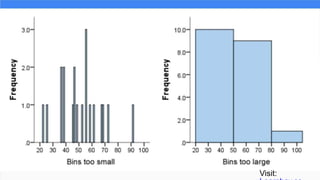
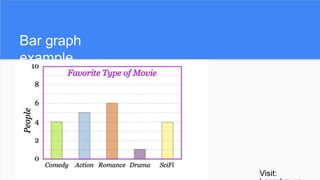
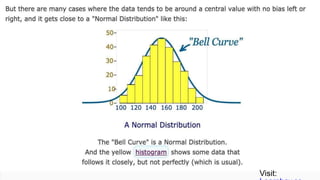
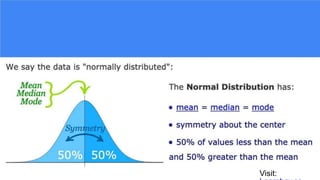
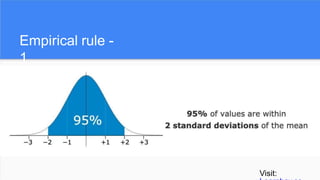
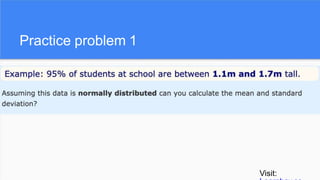
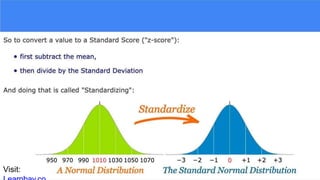
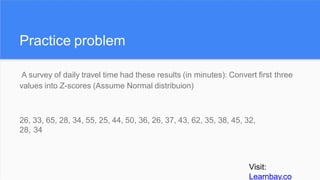
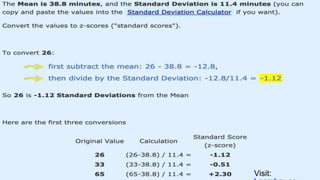
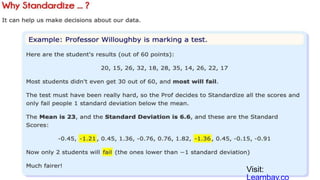
The document provides an overview of histograms and normal distribution, explaining how to plot data using histograms to reveal the underlying frequency distribution. It discusses the importance of bin selection, the relationship between standard deviation and normal distribution, and introduces concepts such as z-scores. Examples and practical problems illustrate these statistical concepts effectively.

1. Histogram & Normal
distribution Practice
Visit:

2. Histogram
Visit:
A histogram is a plot that lets you discover, and show, the underlying frequency
distribution (shape) of a set of continuous data. This allows the inspection of
the data for its underlying distribution (e.g., normal distribution), outliers,
skewness, etc.
36, 25, 38, 46, 55, 68, 72, 55, 36, 38, 67, 45, 22, 48, 91, 46, 52, 61, 58, 55

3. Let’s build histogram
Visit:
36, 25, 38, 46, 55, 68, 72, 55, 36, 38, 67, 45, 22, 48, 91, 46, 52, 61, 58, 55

4. Approach to bins
Visit:
To construct a histogram from a continuous variable you first need to split the
data into intervals, called bins. In the example above, age has been split into
bins, with each bin representing a 10-year period starting at 20 years. Each bin
contains the number of occurrences of scores in the data set that are contained
within that bin. For the above data set, the frequencies in each bin have been
tabulated along with the scores that contributed to the frequency in each bin
(see next):

5. Visit:

6. Choosing the right bins
Visit:
There is no right or wrong answer as to how wide a bin should be, but there are
rules of thumb. You need to make sure that the bins are not too small or too
large. Consider the histogram we produced earlier (see above): the following
histograms use the same data, but have either much smaller or larger bins

7. Visit:

8. BAR
Graph
A Bar Graph (also called Bar Chart) is a graphical display of data using bars of
different heights.

9. Bar graph
example
Visit:

10. Example
1
Visit:

11. Histogram vs Bar graph
Visit:

12. Normal distribution
Visit:

13. Visit:

14. Normal distribution - continued
Visit:
Many things closely follow a Normal Distribution:
● heights of people
● size of things produced by machines
● errors in measurements
● blood pressure
● marks on a test

15. Visit:

16. The Standard Deviation is a measure of how spread out
numbers are
Visit:

17. Empirical rule
Visit:

18. Empirical rule -
1
Visit:

19. Empirical value -
2
Visit:

20. Practice problem 1
Visit:

21. Visit:

22. It is good to know the standard deviation, because we can say that anyvalue
is:
● likely to be within 1 standard deviation (68 out of 100 shouldbe)
● very likely to be within 2 standard deviations (95 out of 100 shouldbe)
● almost certainly within 3 standard deviations (997 out of 1000 shouldbe)
Visit:

23. Standard scores
Visit:
The number of standard deviations from the mean is also calledthe
"Standard Score", "sigma" or "z-score".
What is his Z-score ?

24. Visit:

25. Visit:

26. Practice problem
A survey of daily travel time had these results (in minutes): Convert first three
values into Z-scores (Assume Normal distribuion)
26, 33, 65, 28, 34, 55, 25, 44, 50, 36, 26, 37, 43, 62, 35, 38, 45, 32,
28, 34
Visit:
Learnbay.co

27. Visit:

28. Graphically same data in Z-scores
Visit:

29. Formula for Z-score
Visit:

30. Visit:
Learnbay.co

31. Reference
Visit:
Learnbay.co
https://www.mathsisfun.com/data/standard-normal-distribution.html