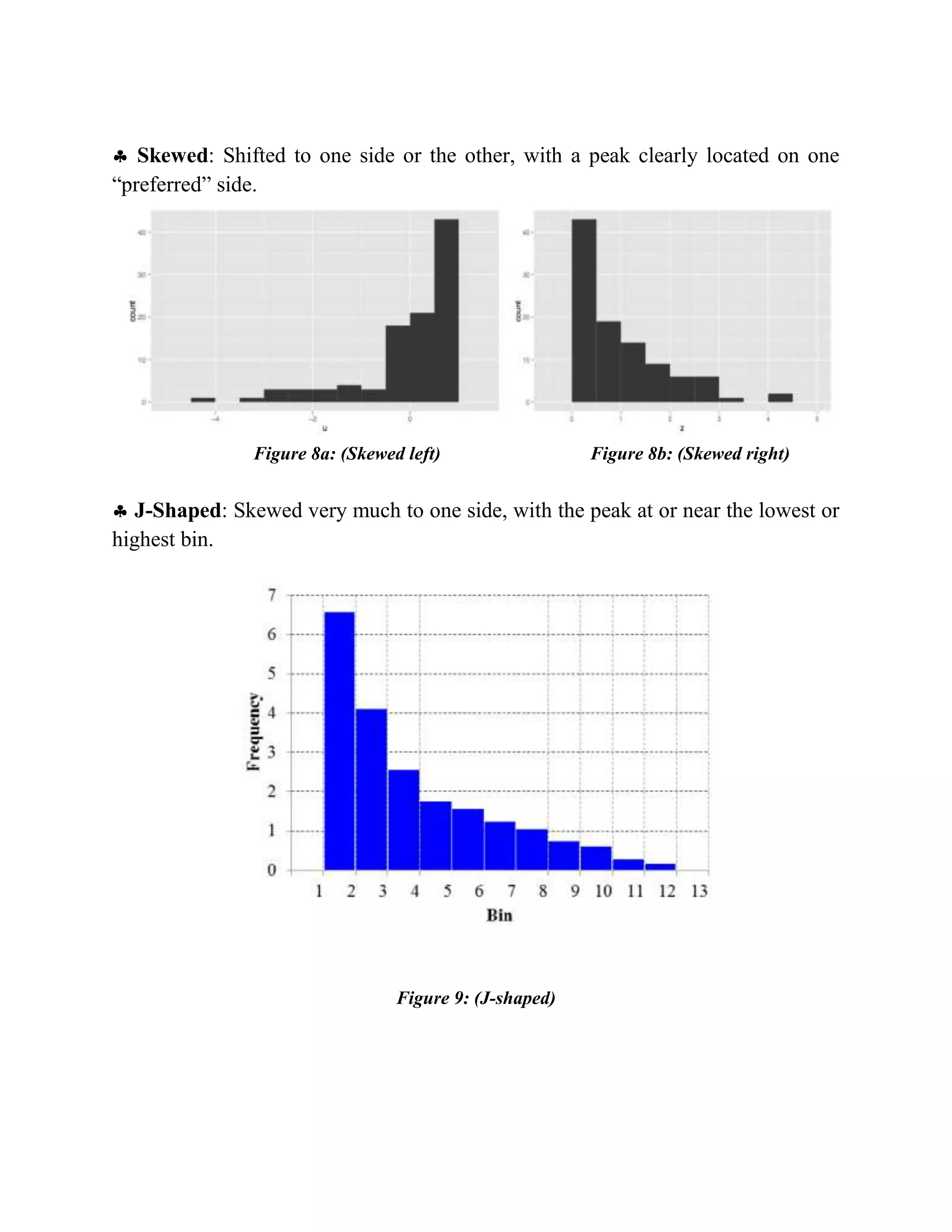
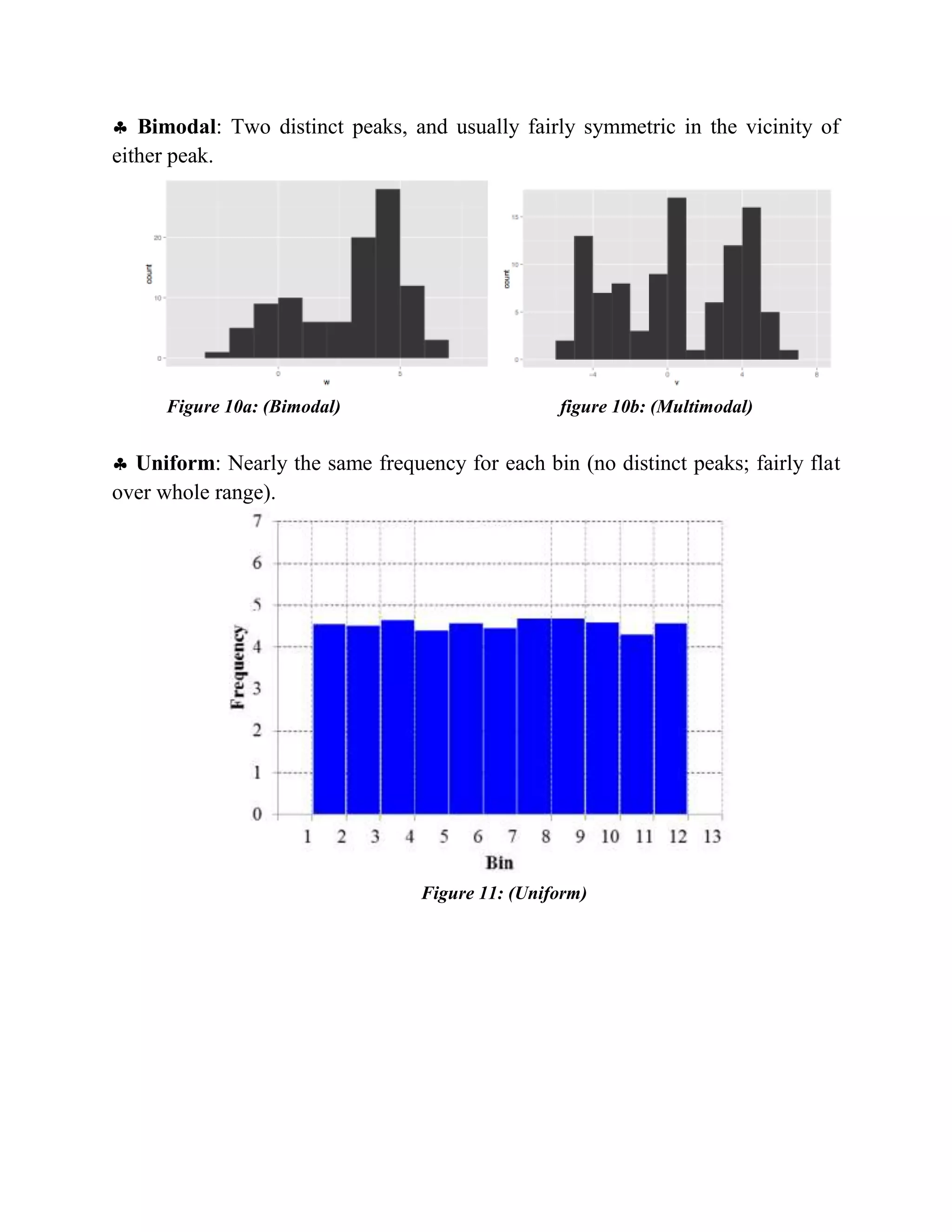
The document discusses different types of histograms used to summarize data distribution. It describes key parts of a histogram including the title, x-axis, y-axis, and bars. Histograms can show normal, bimodal, right-skewed, left-skewed, random, symmetric, skewed, J-shaped, bimodal, and uniform distributions. Standard histogram shapes include symmetric, skewed, J-shaped, bimodal, and uniform distributions. Histograms provide a visual representation of data values and frequency to determine median, distribution, outliers, and gaps in data.

1. UNIVERSITY OF MEDICAL SCIENCE AND TECHNOLOGY
FACULTY OF PHARMACY
DEPARTMENT OF PHARMACEUTICAL CHEMISTRY
M.Sc. Pharmaceutical Analysis and Quality Control
Semester 2
Subject: Total Quality Management
Topic: Different types of Histogram
By: Supervisor
Mohamed Hersi Farah Dr. Sophia Sahal Elmardi
Khartoum-Sudan
08-april-2019

2. Introduction:
A histogram is used to summarize discrete or continuous data. In other words, it
provides a visual interpretation of numerical data by showing the number of data
points that fall within a specified range of values (called “bins”). It is similar to a
vertical bar graph. However, a histogram, unlike a vertical bar graph, shows no
gaps between the bars.
Figure 1: Histogram
Parts of a Histogram
1. The title: The title describes the information included in the histogram.
2. X-axis: The X-axis are intervals that show the scale of values in which the
measurements fall under.
3. Y-axis: The Y-axis shows the number of times that the values occurred
within the intervals set by the X-axis.
4. The bars: The height of the bar shows the number of times that the values
occurred within the interval while the width of the bar shows the interval
that is covered. For a histogram with equal bins, the width should be the
same across all bars.
Importance of a Histogram
Creating a histogram provides a visual representation of data distribution.
Histograms display a large amount of data and the frequency of the data values.
The median and distribution of the data can be determined by a histogram. In
addition, it can show any outliers or gaps in the data.
Distributions of a Histogram:
A normal distribution: In a normal distribution, points on one side of the average
are as likely to occur as on the other side of the average.
Figure 2: Normal Distribution

3. A bimodal distribution: In a bimodal distribution, there are two peaks. In a
bimodal distribution, the data should be separated and analyzed as separate normal
distributions.
Figure 3: bimodal distribution
A right-skewed distribution: A right-skewed distribution is also called a
positively skewed distribution. In a right-skewed distribution, a large number of
the data values occur on the left side with a fewer number of data values on the
right side. A right-skewed distribution usually occurs when the data has a range
boundary on the left-hand side of the histogram. For example, a boundary of 0.
Figure 4: right-skewed distribution
A left-skewed distribution: A left-skewed distribution is also called a negatively
skewed distribution. In a left-skewed distribution, a large number of the data
values occur on the right side with a fewer number of data values on the left side.
A right-skewed distribution usually occurs when the data has a range boundary on
the right-hand side of the histogram. For example, a boundary such as 100.
Figure 5: left-skewed distribution

4. A random distribution: A random distribution lacks an apparent pattern and has
several peaks. In a random-distribution histogram, it can be the case that different
data properties were combined. Therefore, the data should be separated and
analyzed separately.
Figure 6: Random Distribution
Standard types of histograms:
In many cases, the histogram is skewed to one side or may have more than one
peak (e.g., exam grades often produce a strange-looking histogram).
There are five standard histogram shapes that have been given standardized
names:
 Symmetric: Nearly symmetric left to right, with a peak very close to the middle.
Figure 7a: (Symmetric) Figure 7b: (Symmetric, unimodal)

5.  Skewed: Shifted to one side or the other, with a peak clearly located on one
“preferred” side.
Figure 8a: (Skewed left) Figure 8b: (Skewed right)
 J-Shaped: Skewed very much to one side, with the peak at or near the lowest or
highest bin.
Figure 9: (J-shaped)

6.  Bimodal: Two distinct peaks, and usually fairly symmetric in the vicinity of
either peak.
Figure 10a: (Bimodal) figure 10b: (Multimodal)
 Uniform: Nearly the same frequency for each bin (no distinct peaks; fairly flat
over whole range).
Figure 11: (Uniform)