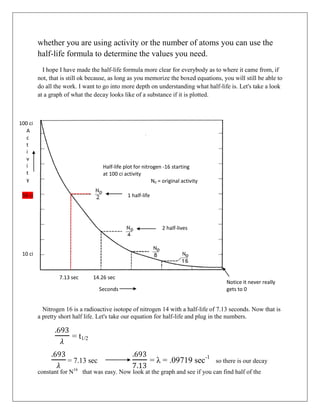
This document provides a detailed derivation and explanation of radioactive half-life formulas. It begins by defining key terms like half-life, radioactive, radiation, decay, activity, and decay constant. It then derives the basic exponential decay formula through calculus. Examples are provided to show how the formula can be used to calculate half-life, decay constant, number of atoms remaining over time, and carbon dating. A sample problem demonstrates using the formulas to determine the age of an ancient Indian site from the percentage of carbon-14 remaining in charcoal.

1. Half-life formula (M J Rhoades)
This is an attachment to the physics cheat sheet
Derivation, how it works, and Carbon dating etc
There seems to be a lot of questions about the half life formulas, how they work, where they
came from, and how to use them. In this paper I hope to answer some of these questions and give
you a better understanding of radioactive half-life. If you do not know what radioactivity is, or
you do not understand what radiation is, go to my paper "Radiation Interactions" on
wepapes.com or scribd and review that first. For this paper I will define a few of the terms that I
will be using throughout the paper as it applies to half-life.
Half-life The term given to the amount of time it takes for half of a substance to radioactively
decay into something else
Radioactive The property or characteristic of a substance to spontaneously decay by the emission
of radiation due to its unstable nucleus
Radiation The energy in particles or waves given off by an unstable nucleus of a radioactive
substance. Now remember these definitions are as they apply to half-life
Decay The spontaneous disintegration process of the nucleus of a radioactive substance
Activity The rate of decay of a radioactive substance
Decay constant (λ) The probability per unit time that an atom will decay
Curie (ci) The unit of measure of the rate of radioactive decay equal to 3.7 x 1010 dis/sec
Becquerel (Bq) Fundamental measure of decay equal to1 disintegration / second
Mole Equals 6.022 x 1023
To understand half-life we must first talk about the relationship between activity, number of
atoms, and the decay constant. This relationship is as follows:
A=λN Where: A = activity of the atoms in disintegrations / sec
λ = the decay constant in second-1 or per second for that type of atom
N = number of atoms present in the sample
Since λ is a constant (remains the same for any particular substance)
Then, A ≈ N this fact will be used later on in the equations.
So what does this mean? Well, it means that the more radioactive stuff of a particular type that
you have, the higher the activity, and that makes perfect since.

2. Now, for those of you who do not understand calculus or dont want to understand calculus,
just move on until the formulas have been derived. I am going to put the "must know" formulas
in boxes. In most cases for high school or college you only need to use the derived formulas. For
engineering students, sorry, you have to know all of it.
Ok, for you future Engineers let's talk about change. If the change in the number of atoms
remaining as the original atom or Nf is dependent on the change in time, then we can write this
as a differential equation which is:
d Nf = - λ Ni dt Where: d Nf = the change in original atom species to final amount
-λ = the decay constant, negative because there will be a
Decrease in the number of original atoms
Ni = the initial number of original atoms species
dt = change in time with respect to the reduction
Dividing both sides by Ni then:
= -λ dt and taking definite integrals both sides
=
0
− do you follow
=- λ 0
remember that constants can move through the integral
final number time final
ln = -λ 0
initial number time 0
ln ( ) - ln ( ) = -λ (tfinal -t0)
ln = - λ tfinal
calculus rule: = ln x + c
= e-λ t

3. -λ t Ok, this is the base formula for the half life formula. All
Nf = N i e of you must know this one because it will be the bases for
all the other formulas
Now if Nf = Ni e-λ t, then lets discuss this a little bit before we start solving again. Let's
review what e is. e is sometimes called Euler's number, Naperian constant, or the natural number
and ln refers to the natural log. The value for e is 2.71828. It comes from a number series which I
am not going to go into. The thing to remember when you are working with e is that:
y = ex and x = loge y Example (use your calculator): say y = 10 then
loge or ln (10) = x = 2.3...
e 2.3... = 10 got it!
In general when working with the equation above you will end up in the form:
ln = -λ t So by taking the natural log (ln) of the ratio of number of atoms
remaining divided by the initial number of atoms, you can determine the decay
constant if you know the time, or time if you know the decay constant !
So let's do an example: Say that the ratio of final number of atoms or substance to the initial
1
number of atoms is ie half- life then: (half the amount has decayed away)
2
1 −.693 .693
ln =-λt - .693 = - λ t = t1/2 = t1/2
2 −
Oh no, look what we have done, there is the half-life formula!
Remember earlier when I said that A (activity) ≈ (Proportional) to N (#of atoms in sample)
A ≈ N Then we can substitute A for N in the equation:
.693
Af = A i e- λ t = e-λ t = t1/2 Oh no, we did
it again, there is the half life formula! The point I am making here is

4. whether you are using activity or the number of atoms you can use the
half-life formula to determine the values you need.
I hope I have made the half-life formula more clear for everybody as to where it came from, if
not, that is still ok because, as long as you memorize the boxed equations, you will still be able to
do all the work. I want to go into more depth on understanding what half-life is. Let's take a look
at a graph of what the decay looks like of a substance if it is plotted.
100 ci
A
c
t
i
v
i Half-life plot for nitrogen -16 starting
t at 100 ci activity
y N0 = original activity
50 ci 1 half-life
2 half-lives
10 ci
7.13 sec 14.26 sec
Notice it never really
Seconds gets to 0
Nitrogen 16 is a radioactive isotope of nitrogen 14 with a half-life of 7.13 seconds. Now that is
a pretty short half life. Let's take our equation for half-life and plug in the numbers.
.693
= t1/2
.693 .693
= 7.13 sec = λ = .09719 sec-1 so there is our decay
7.13
constant for N16 that was easy. Now look at the graph and see if you can find half of the

5. activity. This is the definition for half-life and we can see that 7.13 seconds has gone by. In 14.26
seconds, half of that again has decayed away. After 7 half-lives, the amount of the original
substance (N-16) is considered 0, but it is really not zero because decay is a probability and some
atoms may remain around forever. Ok, let's roll up our sleeves and get to work on a problem. this
is not a simple plug and chug problem but it will show you how all this stuff works. But before
we start, I want to give you some advice. If you are a serious student that is pursuing a scientific
degree, you need to obtain a chart of the nuclides, and you will never get a good printable copy
off the internet. I bought one from the Knolls Atomic Power Laboratory for 25$ US. You can go
online to chart of the nuclides.com and order the wall chart and booklet for 25 or you can get a
booklet with the chart in it (you have to thumb back and forth to find the page with the nuclide
on it, for 25. I personally bought both. The information contained is invaluable for any science or
engineering major. Now, I dont work for them, and I dont get any money from them, I am just
plugging them because they have an outstanding product. And something else, I talked to Dr
Miller who is one of the lead Scientist for this project and he informed me that the energy levels
(Ke) listed for the decay particles was the actual energy of the particle and does not include the
recoil energy of the mother nucleus. That may not mean much to you now, but when you hit your
engineering classes, it will be of great help, trust me. This chart lists every known nuclide, the
half-lives and so much more.
Ok, let's get to our first problem. A 20 microgram sample of Californium 252 has a half-life of
2.646 years. Find:
1) The number of californium-252 atoms initially present
2) The activity of the californium-252 in curies
3) The number of californium-252 atoms that will remain in 12 years
4) The time it will take for the activity to reach 0.001 curies
First you have to go to the chart of the nuclides and find the gram atomic weight which equals
252.08 grams. This is the weight of one mole of atoms. We were given a 20 microgram sample.
So:
-6
1 6.022 10 23
# of atoms = (20 x 10 g) = 4.78 x 1016
252.08 1
atoms
Next we are going to need to calculate the decay constant, so using our half-life formula:
0.693 0.693
λ= = = 0.262 year-1 we now have to convert this to sec-1
1/2 2.646

6. 1 1 1
λ = .262 year-1 = 8.3 x 10-9 sec-1
365.25 24 3600
Ok we now have our decay constant, so what is next? Oh, the activity in curies is the second part
A = λ N Where: A = activity in disintegrations / sec
λ = the decay constant in sec-1
N = the number of atoms
A = (8.3 x 10-9 sec-1) (4.78 x 1016 atoms)
A = 3.97 x 108 disintegrations / sec
this is our answer in Bq, but we need curies right? so
1
A in curies = (3.97 x 108 dis/sec) = 0.01073 curies
3.7 10 10 /
Ok, we have our number of atoms in the original sample; we have the activity in curies, next # of
atoms left after 12 years. Here we are going to need the equation:
Nf = Ni e -λ t
Nf = (4.78 x 1016) (2.17828 - (2.62 / year) (12 years)) Warning! as long as the units
are the same it's ok. Dont
Nf = 2.06 x 1015 atoms remaining mix days with minuets etc, or
you will be wrong
Now for the last part of the problem, the time it will take to reach an activity of 0.001curies.
for this we will need the equation:
Af = Ai e - λ t
ln = - λ t (Remember how we did this earlier) now rearranging the
formula
− 0.001
−
0.01073
t= = = 9.057 years
0.262 −1

7. The nice thing about this problem is that it made us use all the formulas we derived, and if you
have figured this one out, you can do all the rest of the half life problems you will run into.
Let's talk about carbon dating now. It's no harder than the problem we just worked out; you
only need to understand a couple of things about it and it will become clear. Then, we will work
a problem with carbon dating so you understand fully. First of all, the normal run of the mill
carbon is carbon-12, the carbon used in carbon dating is carbon-14. The only reason carbon
dating works at all is because of the carbon-14. Where does carbon-14 come from?
It comes from the atmosphere. It is created in the atmosphere, when incoming cosmic rays
(Neutrons, or free Neutrons caused by other cosmic rays) reacts with a Nitrogen-14 atom. The
high energy Neutron Knocks out a proton in the Nitrogen atom, the Neutron is absorbed by the
now Carbon atom and becomes radioactive Carbon-14 with a half-life of 5,715 years. What's
nice about this half-life, it is good for determining recent life form dates. Let me explain further.
In order for you to get carbon-14 in your body, you must be eating. That is, you are alive. The
trees and plants take in the carbon-14 from the air; (they are alive) you eat the trees and plants, or
the meat from those animals that eat the trees and plants. Carbon-14 comes into equilibrium in
our bodies and in the plants etc. Now, if you or a plant dies, the intake of carbon-14 stops, and
the half-life decay clock starts. get it! So what do you think would happen if you were buried and
dug up 5,715 years later? That's right, 1/2 of the carbon-14 in your body would be gone, and if a
detector especially tuned for reading carbon-14 emission was used, they could tell the day you
died, or pretty close. Do you see how it works? The formula for the production of C-14 is as
follows:
14 14
Neutron + 7 N 6 C + proton
The 614 C emits a 0.157 Mev β- particle to decay back to nitrogen.
Ok let's solve a problem: An ancient Indian site is discovered in Utah, The charcoal in a
camp fire at the site is found to contain only 15% of the C-14 found in fresh charcoal. How old is
the site?
We will need two of the formulas to find the answer, the half-life formula to
determine the decay constant and the number of atoms remaining formula.
0.693 0.693
λ= = = 1.212 x 10-4 years-1 ok there's our decay constant
1/2 5,715
-λt
Nf = Ni e we know that = .15 or 15% as stated in the problem, So:
ln .15 = - λ t
ln .15
= t = 15,652 years I hope this paper helped you out!
1.212 10 −4