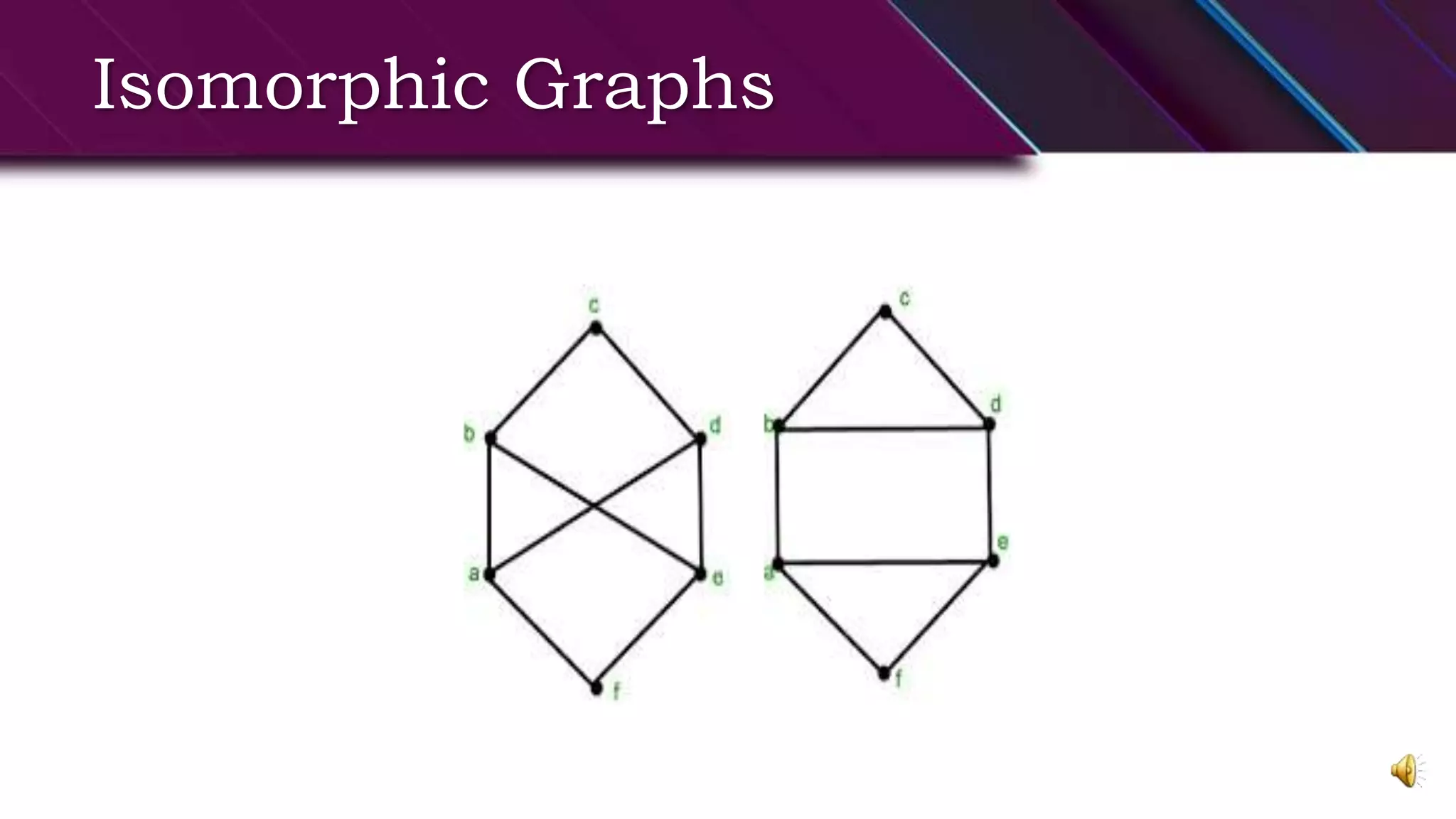
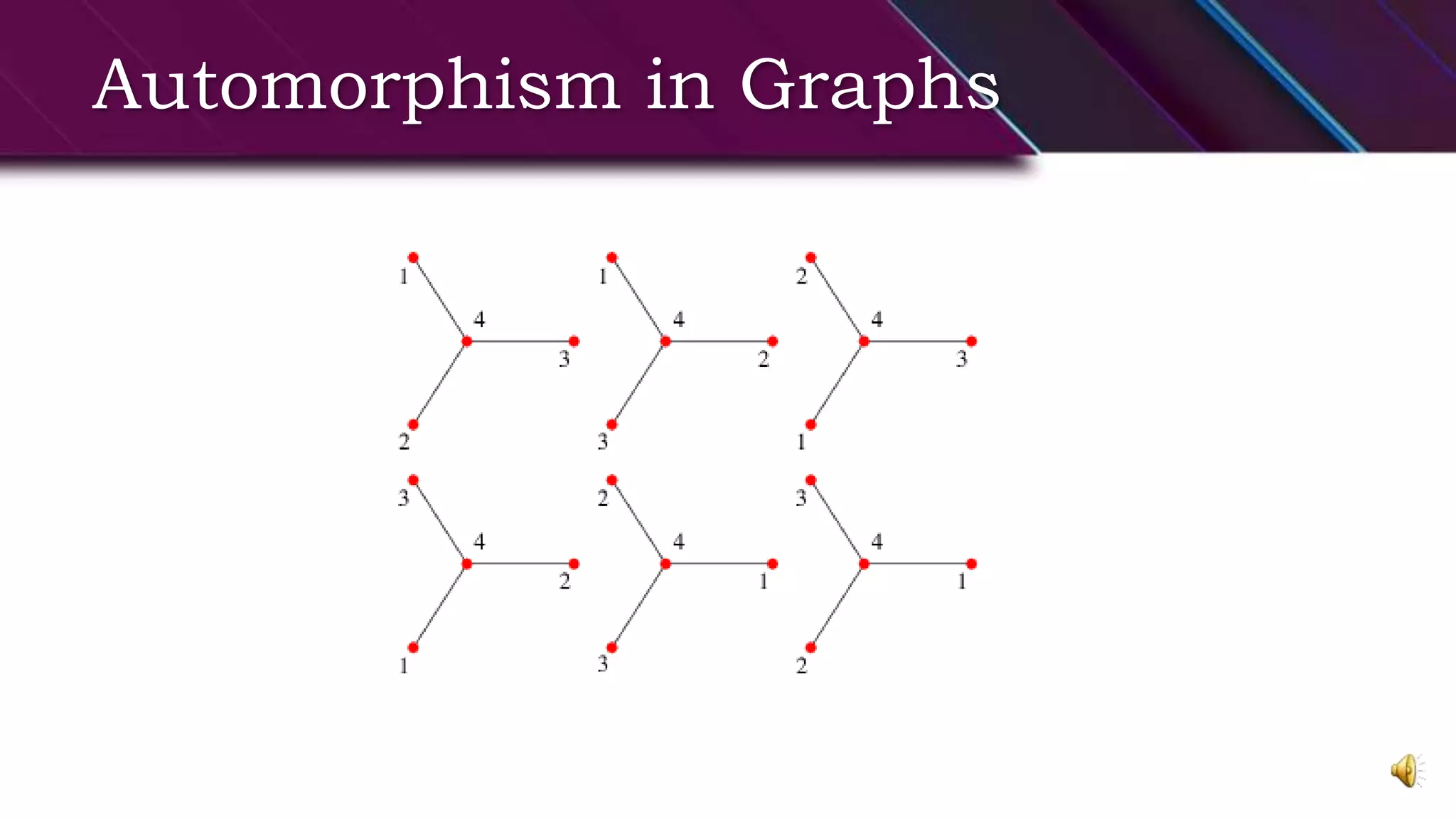
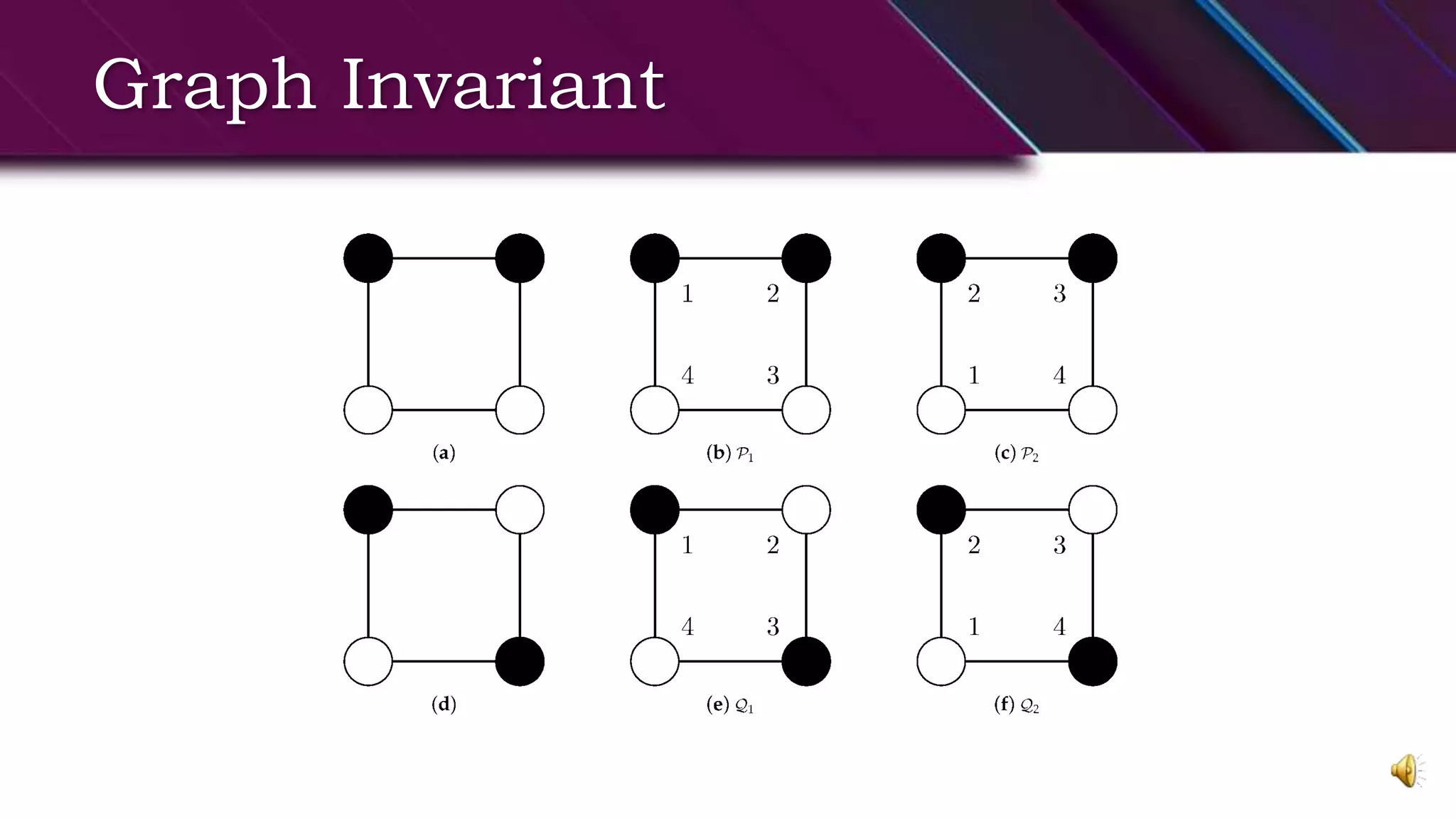
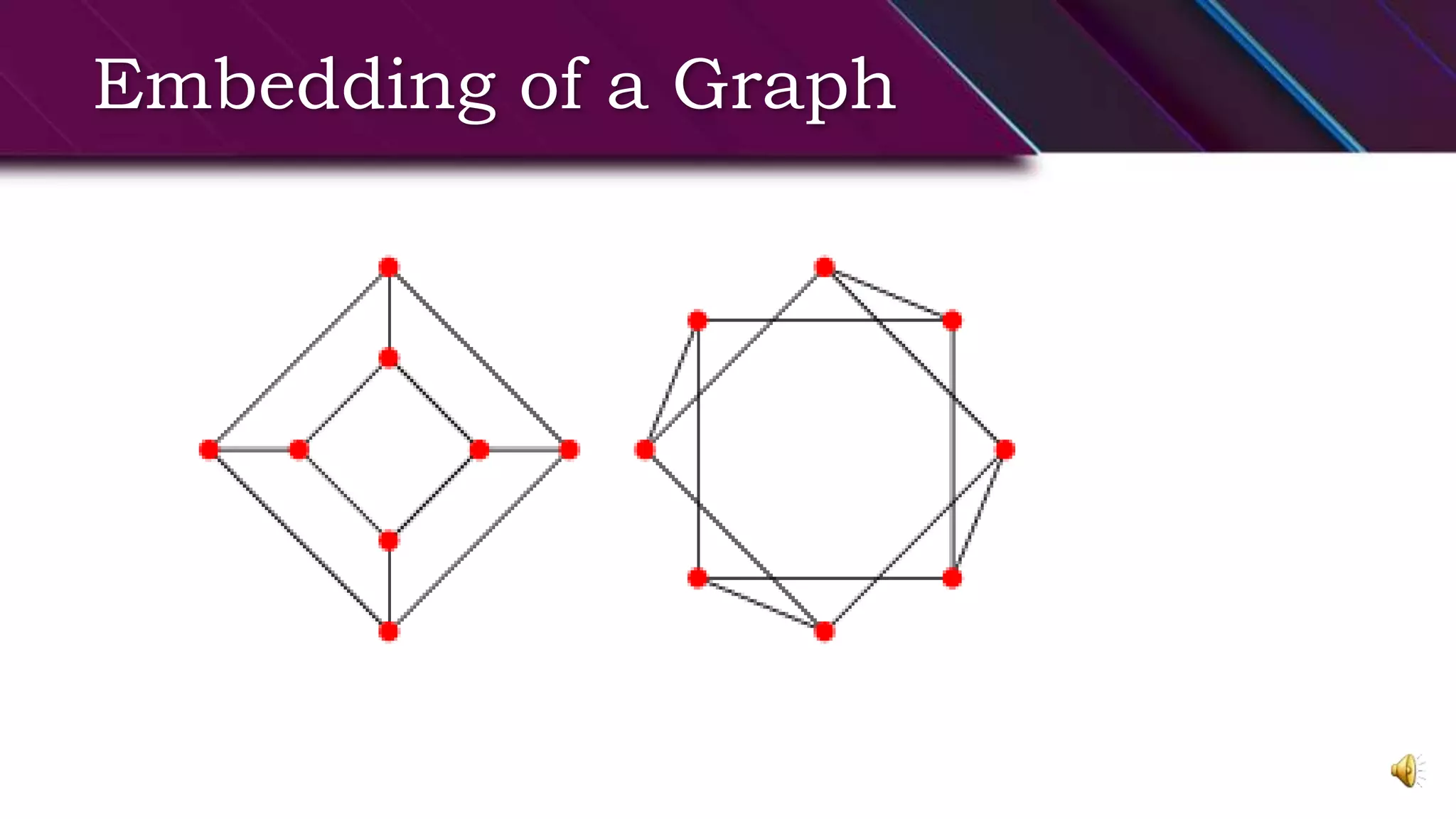
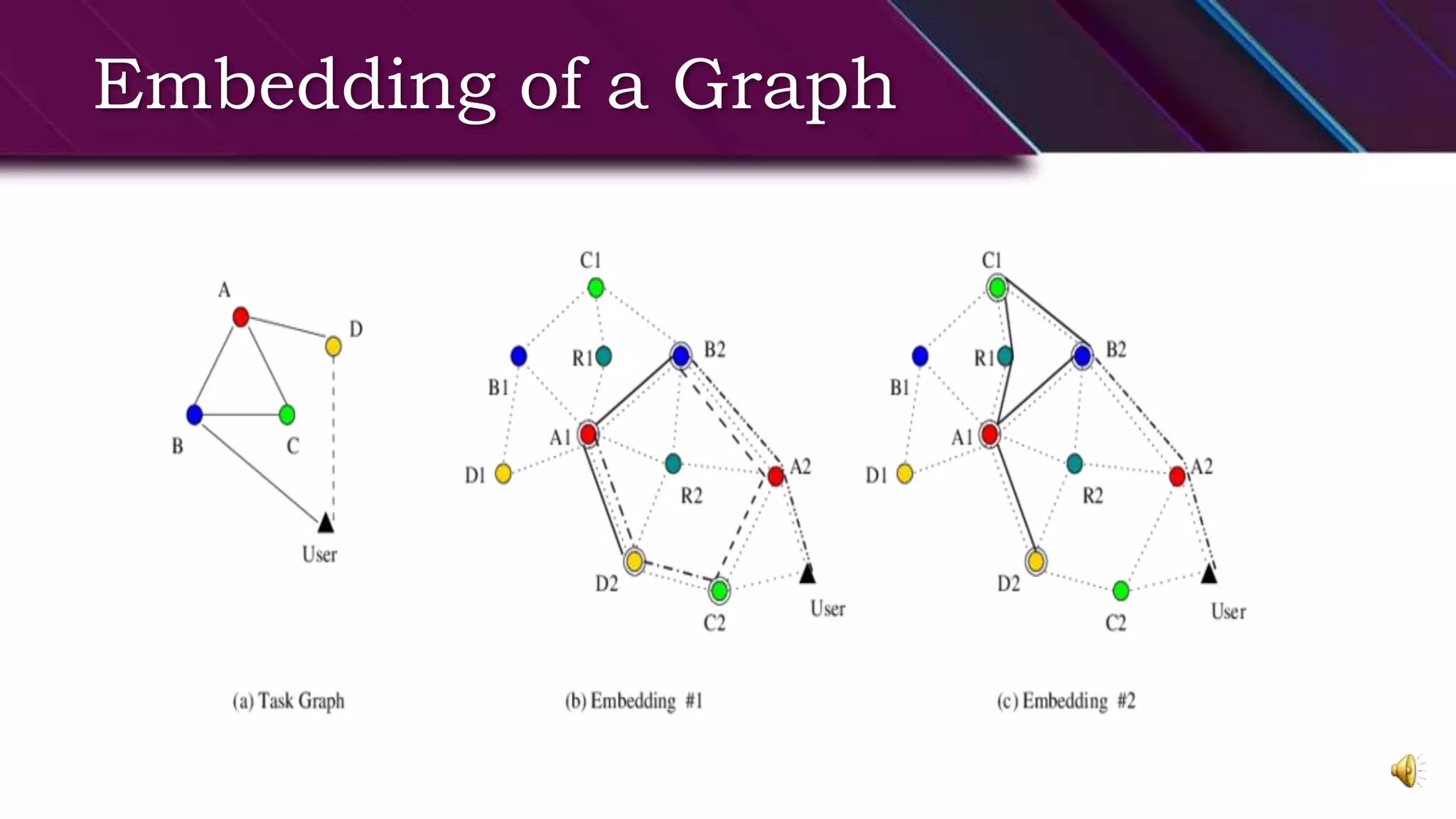
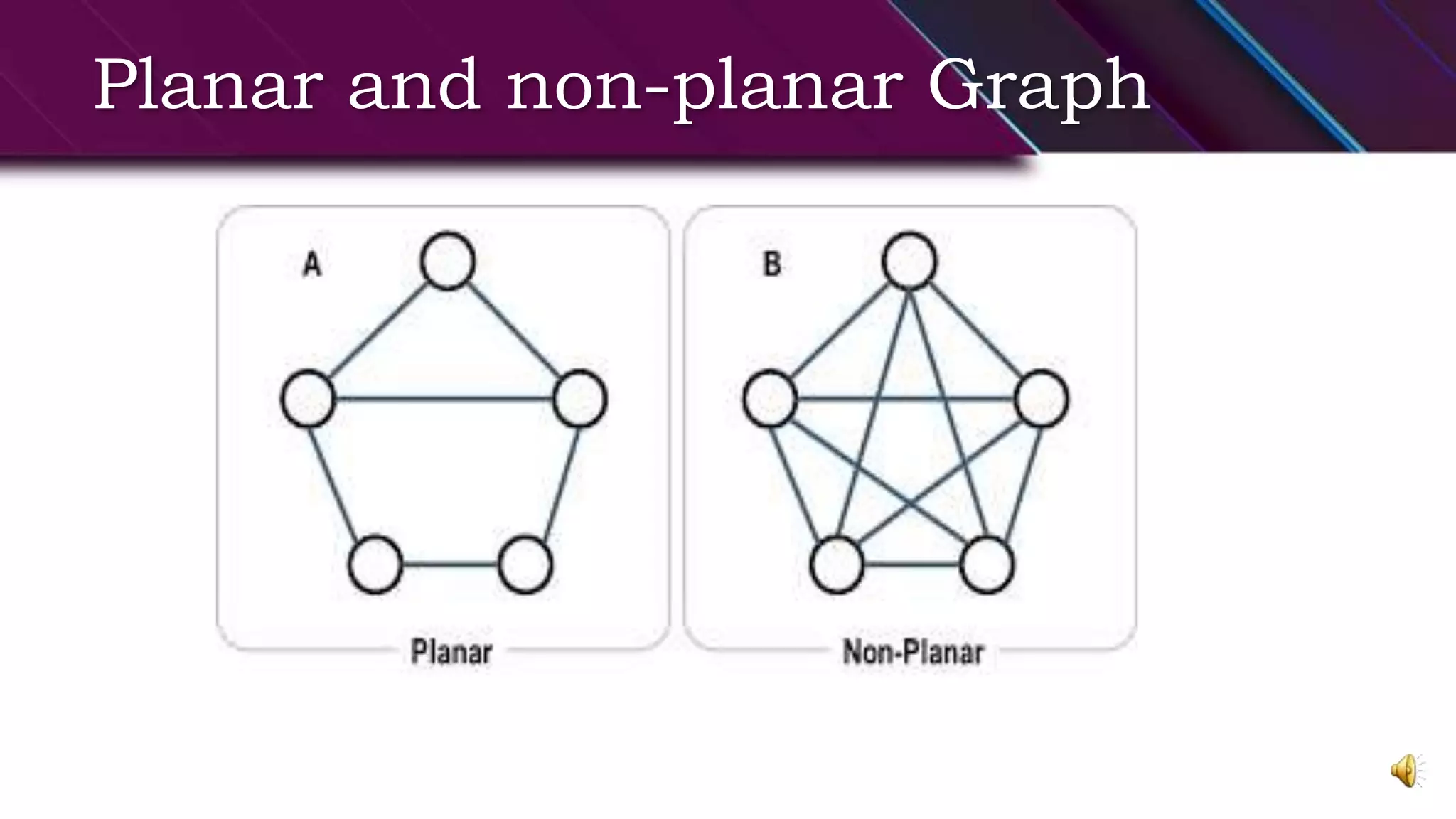
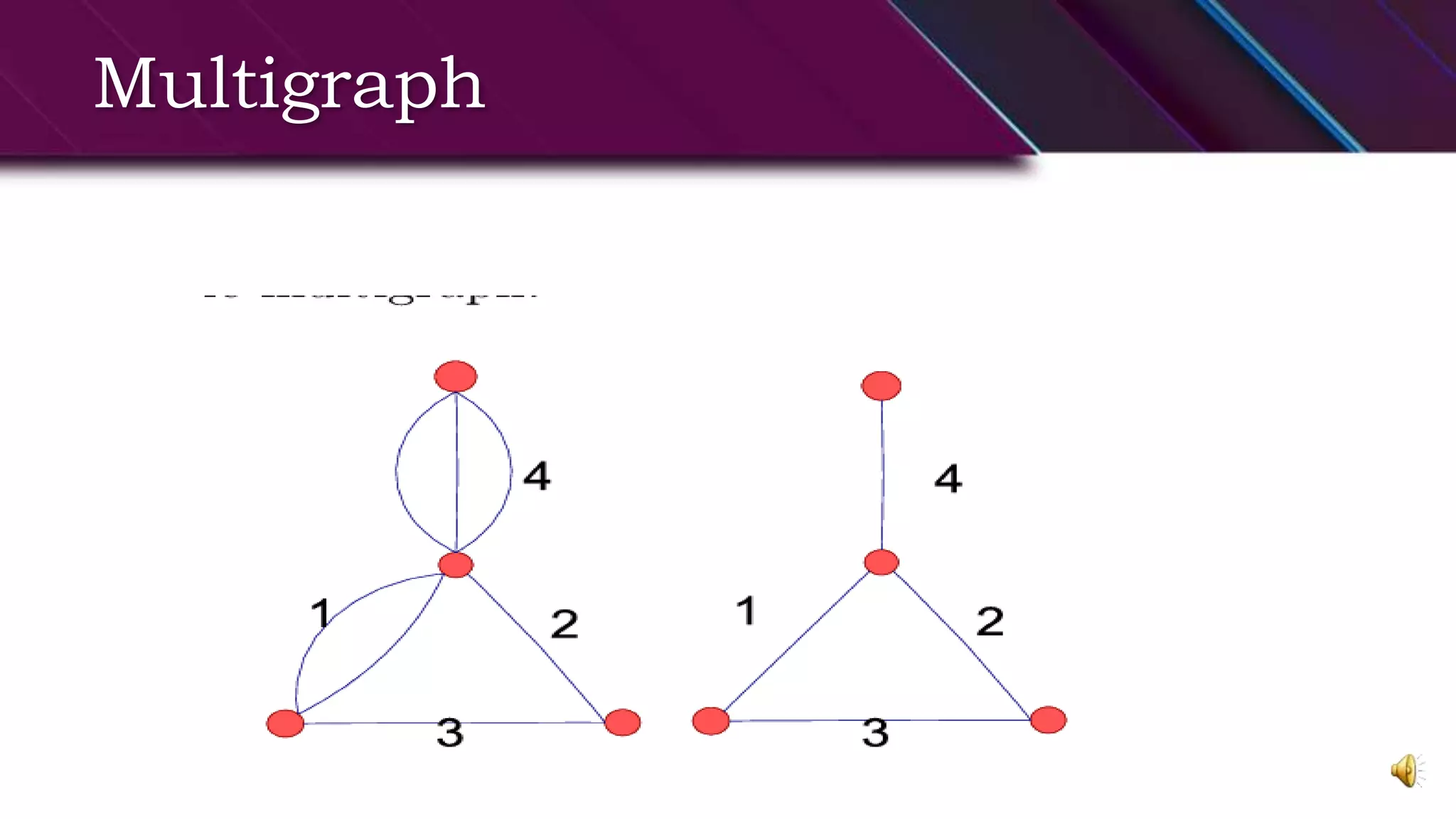
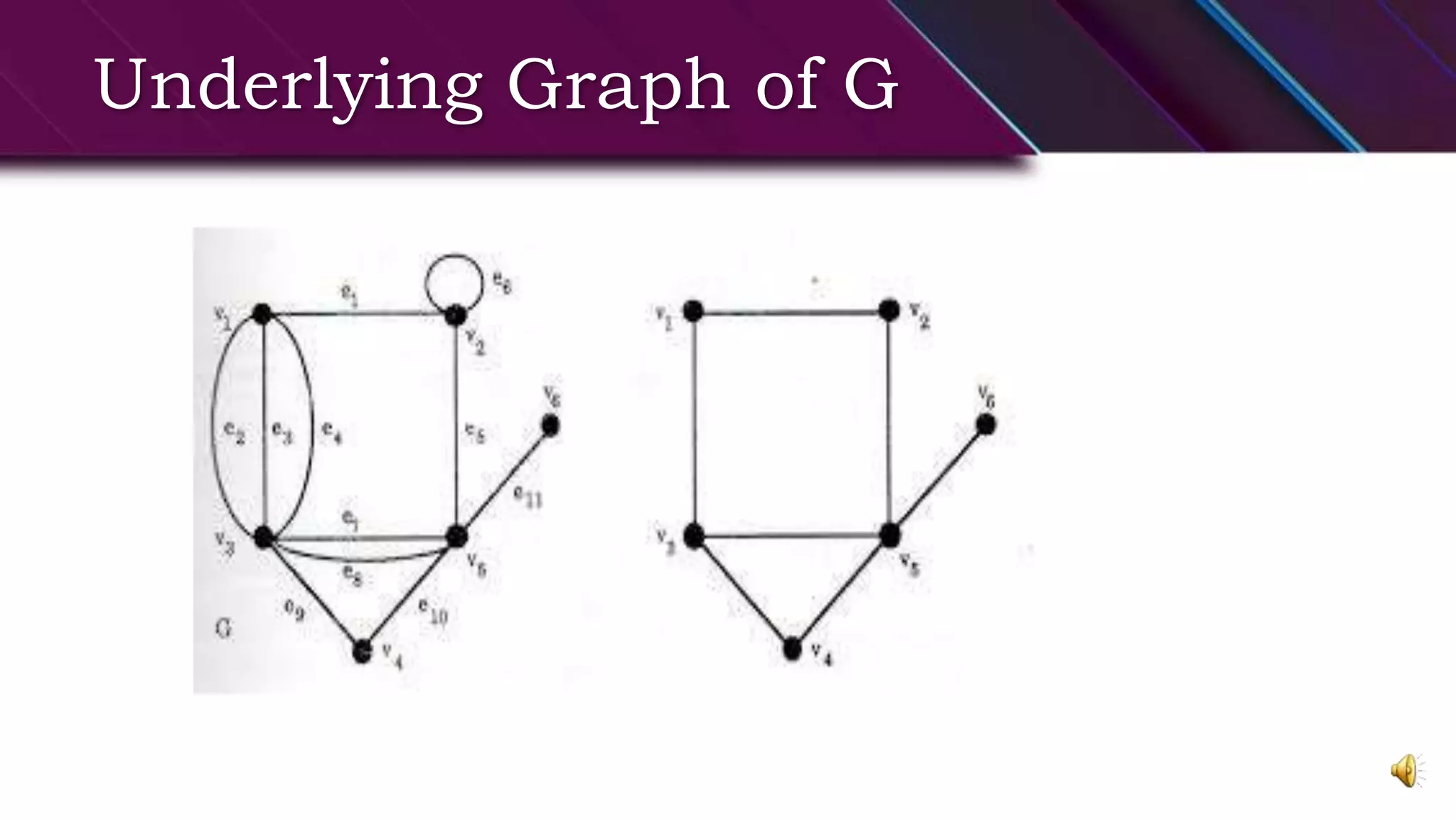
This document provides an overview of basic graph theory concepts. It defines graphs, subgraphs, and some special types of graphs. A graph is defined as a pair of sets (V,E) where V is the set of vertices and E is the set of edges. A subgraph is a graph whose vertex and edge sets are subsets of another graph. Complete graphs, empty graphs, bipartite graphs, and complement graphs are some special types of graphs discussed. The document also introduces concepts like isomorphic graphs, graph embeddings, planar vs. non-planar graphs, multigraphs, digraphs, and operations on graphs like edge/vertex removal.