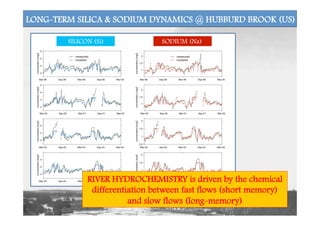
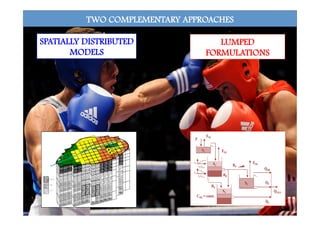
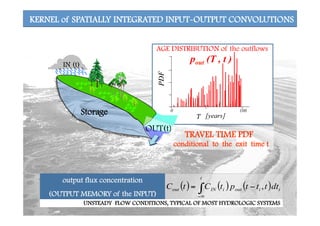
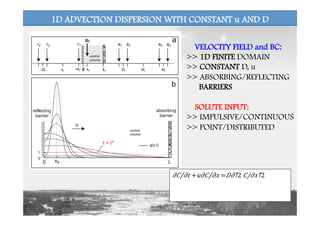
This document discusses storage selection functions (SAS) as a tool for characterizing dispersion processes and solute transport at the catchment scale. SAS functions link the age distributions of water stored in a catchment to the age distributions exported from the catchment. They can be used to derive travel time distributions and model concentrations of conservative solutes. The formulation incorporates temporal variability in hydrologic fluxes and can represent spatial heterogeneity through distinct SAS functions for different catchment units. Case studies demonstrate how SAS functions capture catchment-scale age selection dynamics and can reproduce observed solute concentrations in streams.

1. STORAGE
SELECTION (SAS)
FUNCTIONS:
A
TOOL
FOR CHARACTERIZING DISPERSION PROCESSES AND
CATCHMENT-SCALE SOLUTE TRANSPORT
G. Botter
Dept. Civil & Environmental Engineering, University of Padova (ITALY)
Workshop
on
coupled
hydrological
modling
Padova
|
23
–
24
April
2015

2. RIVER HYDROCHEMISTRY and CATCHMENT SCALE TRANSPORT
…why RIVER HYDROCHEMISTRY ?
Water quality has well known implications for human
well being and ecosystem services
In spite of the huge number of available models and
datasets focused on water fluxes, catchment -scale
transport models/datasets are less widespread
River hydrochemistry provides important clues for
process identification and hydrologic functioning

3. the chemical response is much more “damped” compared to the
hydrologic signal – different processes
HYDROLOGIC vs CHEMICAL SIGNALS
[Kirchner et al.., Nature 2000]

4. THE OLD WATER PARADOX
‘new’ rainfall
discharge‘old’ stored water
the hydrologic response to a rainfall event is chiefly made by water
particles already in storage before the event (old water)

5. THE OLD WATER PARADOX
TRACKS OF PAST RAINFALL EVENTS IN STREAMS…
LASTING FOR MONTHS/YEARS (LONG MEMORY)
EVENT WATER
the hydrologic response to a rainfall event is chiefly made by water
particles already in storage before the event (old water)

6. NON-POINT SOURCES & CATCHMENT-SCALE SOLUTE TRANSPORT
NUTRIENTS
PESTICIDES ECOSYSTEM IMPACTS
SLUDGE SPILLS

7. WATER RESOURCES AND WATER QUALITY
...NOT ONLY BECAUSE OF REDUCED WATER AMOUNTS,
BUT ALSO BECAUSE OF INSUFFICIENT WATER QUALITY
IN MANY REGIONS OF THE WORLD WATER RESOURCES
ARE SHRINKING...

8. THE AGE OF WATER & WATER QUALITY ISSUES
LAND MANAGEMENT AND CATCHMENT RESILIENCE

9. A CHALLENGING PROBLEM...
SPATIAL and TEMPORAL
PATTERNS of SOLUTE INPUT
LANDSCAPE HETEROGENITY
TEMPORAL VARIABILITY
OF CLIMATE FORCING
HYDROLOGIC PROCESSES

10. SPATIALLY DISTRIBUTED
MODELS
LUMPED
FORMULATIONS
TWO COMPLEMENTARY APPROACHES
VS.

11. SPATIALLY DISTRIBUTED
MODELS
LUMPED
FORMULATIONS
TRAVEL
TIMES
TWO COMPLEMENTARY APPROACHES

12. X0
Xt(t;X0,t0)
X1
X3
X2
INJECTION
AREA
CONTROL
VOLUME
Lagrangian transport model:
water parcels traveling through a
control volume
[e.g. Dagan, 1989; Cvetkovic and Dagan, 1994; Rinaldo et al., 1989]
TRAVEL TIME FORMULATION of TRANSPORT
),(
),;( 00
t
dt
ttd
t
t
XV
XX
=
particle’s trajectory:
INPUT
OUTPUT
CONTROL
PLANE CP
KINEMATIC DEFINITION of TRAVEL TIME : CPtTt ∈);( 0XX

13. KERNEL of SPATIALLY INTEGRATED INPUT-OUTPUT CONVOLUTIONS
AGE DISTRIBUTION of the outflows
T
T
OUT(t)
Storage
IN (t)
TRAVEL TIME PDF
conditional to the exit time t
pout (T , t )
( ) ( ) ( )∫∞−
−=
t
iioutiINout dttttptCtC ,
output flux concentration
(OUTPUT MEMORY of the INPUT)
PDF
UNSTEADY FLOW CONDITIONS, TYPICAL OF MOST HYDROLOGIC SYSTEMS

14. THE FOKKER PLANK EQUATION
( )=0|, ttg x
[Benettin, Rinaldo and Botter, WRR 2013]
displacement pdf (injection in t0)
ADVECTION DISPERSION
EULERIAN
CONCENTRATION

15. AGE MASS DENSITY
T
T
T
AGE MASS DENSITY [Ginn, WRR 1999]
...REPRESENTS THE AGE (T) DISTRIBUTION
AT A GIVEN POINT x AND AT A GIVEN TIME t
mass input in
t-T (age T)
displacement
pdf
TIME SPENT INSIDE THE SYSTEM SINCE ENTRY
(ages increase during the parcels’ journey
within the control volume)
AGE OF WATER/SOLUTE PARCEL T

16. SPATIAL INTEGRATION OF THE FOKKER PLANCK EQUATION
AGE PDF IN THE OUTFLOW (TRAVEL TIME PDF):
)(
)(
),(
),(),(
tM
t
tTp
T
tTp
t
tTp out
out
SS φ
−=
∂
∂
+
∂
∂
xx dtT
tM
tTp
V
S ∫= ),,(
)(
1
),( ρ
σρρ dtTttTt
tΦ
tTp
outV
out
out nxxDxxu •∇−= ∫∂
)],,(),(),,(),([
)(
1
),(
SPATIALLY AVERAGED MASS AGE CONSERVATION
AGE PDF IN THE STORAGE:
...as a function of spatially integrated fluxes and storage
[Botter et al., GRL 2011]

17. The particles leaving the system are sampled among those in storage,
and so their age:
ω(T, t)pout (T,t) = pS(T, t)
PREFERENCE
StorAGE
SELECTION
FUNCTION
LOW AVAILABILITY or LOW PREFERENCE IMPLIES LOW SAMPLING
– AGES POORLY REPRESENTED IN THE OUTPUT
[Botter et al., GRL 2011]
OUT(t)
pout(T,t)
pS(T, t)
AGES SAMPLED AGES AVAILABLE
StorAGE selection: LINKING AGE DISTRIBUTIONS

18. The particles leaving the system are sampled among those in storage,
and so their age:
1
SAMPLING
through
SAS
func?ons
1
1
uniform
preference
over
all
ages
ω decreases
for
older
ages
𝝎(𝑻, 𝒕)
𝝎(𝑻, 𝒕)
𝝎(𝑻, 𝒕)=const
ω
increases
for
older
ages
random sampling
preference for old water
preference for new water
T
T
𝑻
𝝎
𝝎
𝝎
ω(T, t)pout (T,t) = pS(T, t)
AGES AVAILABLE PREFERENCE
StorAGE
SELECTION
FUNCTION
StorAGE selection: LINKING AGE DISTRIBUTIONS
AGES SAMPLED

19. SAS as SPATIALLY INTEGRATED DESCRIPTORS of TRANSPORT
SAS seen from a full 3D KINEMATIC FORMULATION ...
SURFACE INTEGRAL: flux of
ages across the boundaries
VOLUME INTEGRAL: ages stored
T
[Benettin, Rinaldo and Botter, WRR 2013]

20. 1D ADVECTION DISPERSION WITH CONSTANT u AND D
VELOCITY FIELD and BC:
>> 1D FINITE DOMAIN
>> CONSTANT D, u
>> ABSORBING/REFLECTING
BARRIERS
SOLUTE INPUT:
>> IMPULSIVE/CONTINUOUS
>> POINT/DISTRIBUTED
​ 𝜕 𝐶/𝜕𝑡 + 𝑢​ 𝜕 𝐶/𝜕𝑥 = 𝐷​​ 𝜕↑2 𝐶/𝜕​ 𝑥↑2

21. 1D CONVECTION DISPERSION WITH CONSTANT u AND D
normalized age
SASSASPDFPDF
STORAGE SELECTION FUNCTION
STORAGE SELECTION FUNCTION
STORAGE
OUTFLOW
AGE DISTRIBUTIONS and
SAS FUNCTIONS for
POISSON INPUTS
(...for selected times, but SAS
are almost stationary)
normalized age

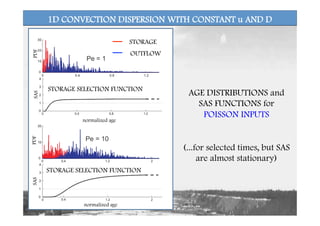
22. STORAGE SELECTION FUNCTIONS AND PECLET NUMBER
normalized age [%]
ω(T)
STORAGE SELECTION FUNCTIONS FOR DIFFERENT DEGREE OF DISPERSION
HIGH DISPERSION COEFFICIENTS (low Pe) INCREASES
UNIFORMITY OF SAS (- RANDOM SAMPLING)

23. SPATIAL PATTERNS of CONCENTRATION and SAS FUNCTIONS
SPATIAL PATTERNS of
CONCENTRATION
..for low Pe:
C_out = mean C in (0,L)
BUT
NOT A WELL MIXED
SYSTEM
storAGE selection
[Benettin, Rinaldo and Botter, WRR 2013]
RANDOM SAMPLING
normalized age
CONCENTRATION PROFILE

24. SPATIALLY DISTRIBUTED INJECTIONS AND SAS FUNCTIONS
SPATIALLY DISTRIBUTED INJECTIONS... INCREASE SAS UNIFORMITY
storAGE selection function (SAS)
RANDOM SAMPLING
normalized age

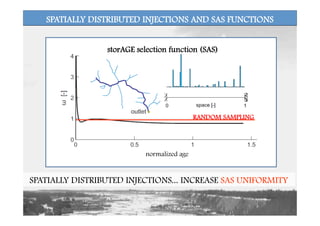
25. WHY SHOULD WE CARE ABOUT SAS FUNCTIONS?
)(
)(
),(
),(),(
tM
t
tTp
T
tTp
t
tTp out
out
SS φ
−=
∂
∂
+
∂
∂
),(),(),( tTptTtTp Sout ω=
>> derive ps(T,t) and pout(T,t) for water based on SAS
and integral fluxes/storage
( ) ( ) ( )∫∞−
−=
t
iioutiINout dttttptCtC ,
>> water age distributions can be used to compute
concentrations of conservative (or reactive) solutes:
SPATIALLY AVERAGED MASS AGE CONSERVATION
{
[Botter et al., GRL 2011; Botter WRR 2012; Rinaldo et al., WRR 2011]

26. WHY SHOULD WE CARE ABOUT SAS FUNCTIONS?
)(
)(
),(
),(),(
tM
t
tTp
T
tTp
t
tTp out
out
SS φ
−=
∂
∂
+
∂
∂
),(),(),( tTptTtTp Sout ω=
>> derive ps(T,t) and pout(T,t) for water based on SAS
and integral fluxes/storage
( ) ( ) ( )∫∞−
−=
t
iioutiINout dttttptCtC ,
>> water age distributions can be used to compute
concentrations of conservative (or reactive) solutes:
SPATIALLY AVERAGED MASS AGE CONSERVATION
{
[Botter et al., GRL 2011; Botter WRR 2012; Rinaldo et al., WRR 2011]
RANDOM SAMPLING: ANALYTICAL
SOLUTIONS

27. ADVANTAGES of THE FORMULATION
DRY WET
INCORPORATES THE TIME VARIABILITY
of HYDROLOGIC FLUXES (dynamic TTDs)
10/2007 11/2007
DISCHARGE[mm/h]CONCENTRATION[mg/l]
SILICA
CHLORIDE
(data from UHF @ Plynlimon, UK)
Late
OCT 2007
INPUT
Mid
NOV 2007

28. DIRECT INTEGRATION OF HYDROLOGIC AND CHEMICAL DATA/MODELS
INCORPORATES THE TIME VARIABILITY
of HYDROLOGIC FLUXES (dynamic TTDs)
ADVANTAGES of THE FORMULATION

29. «CREATION» OF UNAVAILABLE AGES IS NOT ALLOWED reducing
the risk of getting the right answer for the wrong reason
DIRECT INTEGRATION OF HYDROLOGIC AND CHEMICAL DATA/MODELS
INCORPORATES THE TIME VARIABILITY
of HYDROLOGIC FLUXES (dynamic TTDs)
ADVANTAGES of THE FORMULATION

30. DIRECT INTEGRATION OF HYDROLOGIC AND CHEMICAL DATA/MODELS
SPATIAL HETEROGENEITY
CAN BE REPRESENTED
«CREATION» OF UNAVAILABLE AGES IS NOT ALLOWED reducing
the risk of getting the right answer for the wrong reason
INCORPORATES THE TIME VARIABILITY
of HYDROLOGIC FLUXES (dynamic TTDs)
ADVANTAGES of THE FORMULATION

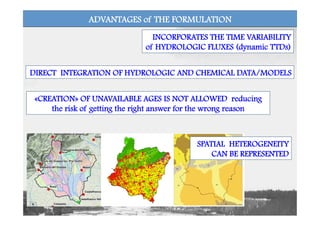
31. INCLUDING SPATIAL HETEROGENEITY
Identify distinct INTERNAL UNITS (VERTICAL and/or HORIZONTAL
HETEROGENEITY) and then define UNIT-SCALE SAS FUNCTIONS
𝝎1(T) (unit 1)
1(T) (unit 1)
[see e.g. Birkel et al., WRR 2014; HP 2015]
𝝎2(T) (unit 2)
2(T) (unit 2)
𝝎3(T) (unit 3)
3(T) (unit 3)
Bruntland Burn(UK): ongoing work in collaboration with C. Soulsby and D. Tetzlaff

32. SAS-BASED LUMPED HYDROCHEMICAL MODEL @ PLYNLIMON (UK)
SERIES OF TWO
STORAGES WITH
UNIFORM SAS
+
LUMPED
HYDROLOGIC
MODEL
OBSERVED
ROOT ZONE
GROUNDWATER
OBSERVED
MODEL
CHLORIDECONCENTRATIONDISCHARGE
[Benettin et al., WRR 2015]

33. DYNAMICAL AGE SELECTION @ PLYNIMON (UK)
CATCHMENT-
SCALE
AGE SELECTION
is controlled by
the catchment
«STATE»
StorAGE SELECTION FUNCTIONS
YOUNG
OLD
normalized age
ω
[Benettin, Kirchner, Rinaldo and Botter, WRR 2015]

34. DYNAMICAL AGE SELECTION @ PLYNIMON (UK)
CATCHMENT-
SCALE
AGE SELECTION
is controlled by
the catchment
«STATE»
FAST flows
(young)
StorAGE SELECTION FUNCTIONS
YOUNG
OLD
normalized age
ω
[Benettin, Kirchner, Rinaldo and Botter, WRR 2015]
INPUT
Mid
NOV 2007

35. DYNAMICAL AGE SELECTION @ PLYNIMON (UK)
StorAGE SELECTION FUNCTIONS
YOUNG
OLD
normalized age
ω
[Benettin, Kirchner, Rinaldo and Botter, WRR 2015]
Late
OCT 2007
CATCHMENT-
SCALE
AGE SELECTION
is controlled by
the catchment
«STATE»
FAST flows
(young)
vs
GW flows
(older)

36. OBSERVED AND MODELED Cl CONCENTRATIONS @ HUPSEL BROOK
SHORT TERM FLUCTUATIONS RELATED TO
THE ROOT ZONE (short travel times)
in WINTER the Cl concentration is sustained by GW (long travel times)
[Benettin et al., WRR 2013]

37. ATRAZINE CONCENTRATIONS @ MONCHALTORF (CH)
OBSERVED
MODEL
[Bertuzzo et al., AWR 2013]

38. LONG-TERM SILICA & SODIUM DYNAMICS @ HUBBURD BROOK (US)
RIVER HYDROCHEMISTRY is driven by the chemical
differentiation between fast flows (short memory)
and slow flows (long-memory)
SILICON (Si) SODIUM (Na)

39. CONCLUDING REMARKS
High dispersion coefficients in 1D
advection – disersion models lead
to uniform SAS (random sampling)
Use of spatially distributed models to analyze
SAS dynamics .. implications for lumped
catchment-scale hydrochemical models
Storage selection functions (SAS) are effective spatially
integrated descriptors of mixing/dispersion
processes in heterogeneous media
The method provides consistent results
in diverse settings (climate, solutes)

40. ACKNOWLEDGMENTS
K. McGuire, J. Kirchner
D. Tetzlaff, C. Soulsby
Andrea Rinaldo, Paolo Benettin, Enrico Bertuzzo
...more details will be provided by Paolo Benettin tomorrow ...