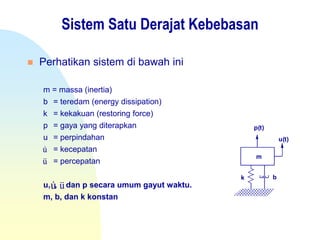
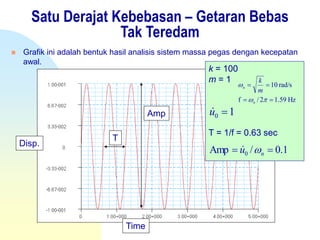
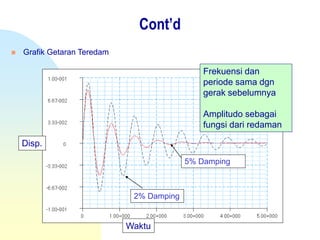
Dokumen ini membahas konsep getaran mekanik pada sistem satu derajat kebebasan, mencakup teori gerak, analisis getaran bebas tak teredam, dan damped free vibrations. Terdapat penjelasan mendetail tentang frekuensi alami, kondisi redaman, serta solusi untuk sistem teredam yang mencakup critically damped, overdamped, dan underdamped. Ringkasan juga menyentuh penerapan gaya harmonik dan analisis respons awal pada sistem yang teredam.

1. Getaran Mekanik
Review Konsep Getaran Mekanik

2. Sistem Satu Derajat Kebebasan
 Perhatikan sistem di bawah ini
m = massa (inertia)
b = teredam (energy dissipation)
k = kekakuan (restoring force)
p = gaya yang diterapkan
u = perpindahan
= kecepatan
= percepatan
u, , dan p secara umum gayut waktu.
m, b, dan k konstan
m
k b
p(t)
u(t)
u
u
u
u

3.  Beberapa teori:
 Persamaan gerak:
 Tak teredam, analisis getaran bebas, persamaan gerak menjadi
lebih sederhana:
 Memiliki penyelesaian:
 Bentuk ini mendefinisikan gerakan harmonik, yang memiliki frekuensi
resonan:
)()()()( tptkutubtum  
0)()(  tkutum 
tBtAtu nn
 cossin)( 
n
Cont’d

4. Sistem Getaran Bebas Tak Teredam Satu
Derajat Kebebasan
 Untuk sistem ini frekuensi alami dirumuskan dengan:
 Penyelesaian keadaan khusus:
m
k
n

n
nn
nnnn
n
tu
A
tBt
tBtAtu
u(tBtt




)0(
dan0)sin(,0Ketika
sincos)(
:an turunanPenyelesai
)0dan0)sin(,0Ketika







tut
u
tu nn
n


cos)0(sin
)0(
)( 


5. Satu Derajat Kebebasan – Getaran Bebas
Tak Teredam
 Grafik ini adalah bentuk hasil analisis sistem massa pegas dengan kecepatan
awal.
Time
Disp.
k = 100
m = 1
T = 1/f = 0.63 sec
Hz59.12/f
rad/s10




n
n
m
k
10 u
T
Amp
1.0/Amp 0  nu 

6. Satu Derajat Kebebasan – Sistem
Teredam
 Jika getaran teredam, maka bentuk persamaan
geraknya menjadi:
 Ada 3 solusi yaitu:
 Critically Damped
 Overdamped
 Underdamped
0)()()(  tkutubtum 

7. Cont’d
 Pada kasus critically damped, tidak ada osilasi, hanya gerak
yang meluruh dari kondisi awal:
 Redaman pada kasus ini, didefinisikan sebagai:
 Disebut overdamped jika b > bcr
 Kondisi sisanya - underdamped
ncr mkmbb 22 
mbt
eBtAtu 2/
)()( 


8. DAMPED FREE VIBRATION SDOF (Cont.)
 Untuk underdamped yaitu b < bcr dan bentuk penyelesaian:
 mewakili frekuensi alami sistim
 idisebut ratio kritis teredam dan didefinisikan dengan:
 Kebanyakan hasil kurang dari 0,1 (10%) jadi
)cossin()( 2/
tBtAetu dd
mbt
  
d
2
1   nd
cr
b
b



nd  

9.  Grafik Getaran Teredam
Frekuensi dan
periode sama dgn
gerak sebelumnya
Amplitudo sebagai
fungsi dari redaman
2% Damping
5% Damping
Cont’d
Waktu
Disp.

10. Redaman Dengan Dikenai Getaran Gaya
 diterapkan fungsi gaya harmonik:
 Catatan adalah frekuensi PENGGERAK atau INPUT
 Persamaan geraknya menjadi
 Penyelesaian terdiri dari dua kondisi:
 Respon awal, karena kondisi awal yang amplitudonya meluruh secara tajam seperti
kondisi sebelumnya:
 Tingkat stabil:
tp sin
tptkutubtum sin)()()(  
22
2
2
)/2()1(
)sin(
/)(
n
n
t
kptu








2
2
1
1
/2
tan
n
n





 

11. Jika sistem teredam diisi dengan fungsi
eksponensial dari frekuensi tunggal,
jumlah seluruh osilasi disebut harmonik:
Osilasi Harmonik

12. Cont’d

13. TERIMA KASIH

14. UJIAN UTS
 Sifat:
 Closed Book
 Pelajari contoh soal yang ada di power point
 Pelajari sistem getaran teredam