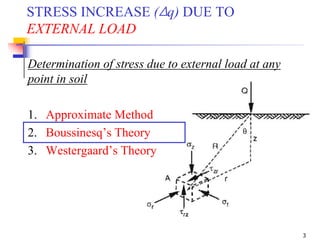
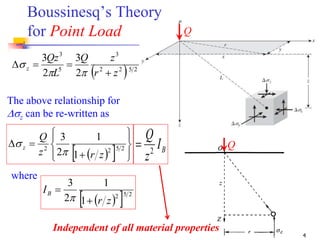
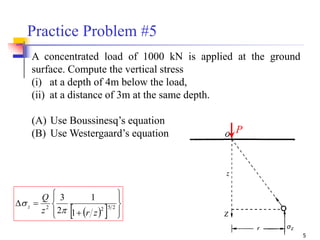
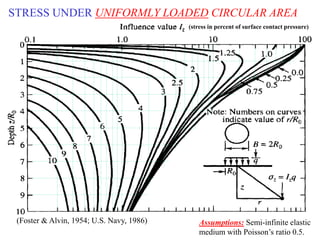
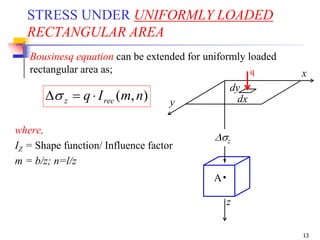
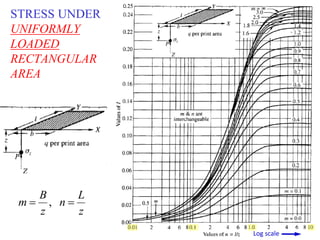
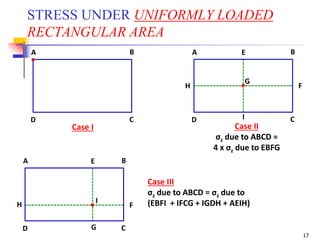
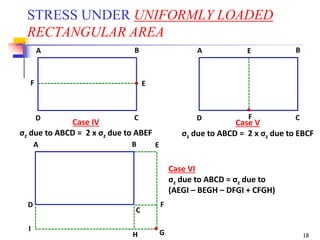
This document is a lecture handout on geotechnical engineering, specifically focusing on stress distribution in soil caused by self-weight and external loads. It includes various theories such as Boussinesq's and Westergaard's equations to calculate stress increases due to point and line loads, as well as uniformly loaded areas. The handout also presents practical problems to illustrate these concepts and methods for determining vertical stress at various depths.

1. 1
Geotechnical Engineering–II [CE-321]
BSc Civil Engineering – 5th Semester
by
Dr. Muhammad Irfan
Assistant Professor
Civil Engg. Dept. – UET Lahore
Email: mirfan1@msn.com
Lecture Handouts: https://groups.google.com/d/forum/geotech-ii_2015session
Lecture # 7A
28-Sep-2017

2. 2
STRESS DISTRIBUTION IN SOIL
What causes stress in soil?
Two principle factors causing
stresses in soil.
1. Self weight of soil
2. External loads (Structural loads,
external load, etc.)
v
h


3. 3
STRESS INCREASE (∆q) DUE TO
EXTERNAL LOAD
Determination of stress due to external load at any
point in soil
1. Approximate Method
2. Boussinesq’s Theory
3. Westergaard’s Theory

4. 4
Q
  2522
3
5
3
2
3
2
3
zr
zQ
L
Qz
z




The above relationship for
z can be re-written as
   








 2522
1
1
2
3
zrz
Q
z


where
   252
1
1
2
3
zr
IB



QBI
z
Q
2

Independent of all material properties
Boussinesq’s Theory
for Point Load

5. 5
Practice Problem #5
A concentrated load of 1000 kN is applied at the ground
surface. Compute the vertical stress
(i) at a depth of 4m below the load,
(ii) at a distance of 3m at the same depth.
(A) Use Boussinesq’s equation
(B) Use Westergaard’s equation P
   








 2522
1
1
2
3
zrz
Q
z



6. 6
Vertical Stress caused by Line Load
x
z
z
z
Q/unit length
x
A
y
By integrating the point load equation along a line, stress due
to a line load (force per unit length) may be found.
Lz I
z
q

 
2
2
/1
12








zx
IL

Where,
q is line load in “per unit length”

7. 7
Practical Problem #6
Following figure shows two line loads and a point load acting
at the ground surface. Determine the increase in vertical stress
at point A, which is located at a depth of 1.5 m.
Q = 10000 kN
z
2 m
A
1.5 m
2 m
3 m
q2 = 250 kN/m q1 = 150 kN/m
   








 2522
1
1
2
3
zrz
Q
z


   








 22
/1
12
zxz
q
z


Point Load
Line Load

8. 8
STRESS INCREASE (∆q) DUE TO
EXTERNAL LOAD
 Point load
 Line Load
• But engineering loads typically act on areas and
not points or lines.
• Bousinesq solution for line load was thus
integrated for a finite area
Bz I
z
Q
2

Lz I
z
q

Uniformly Loaded
Circular Area
Uniformly Loaded
Rectangular Area
Trapezoidal,
Triangular, etc.

9. 9
z
RO
STRESS UNDER UNIFORMLY LOADED
CIRCULAR AREA
Case-A: Vertical stress under the center of
circular footing
   






 232
1
1
1
zR
q
o
z
Boussinesq equation can be extended to a uniformly loaded
circular area to determine vertical stress at any depth.
where,
q = UDL (load/area)
RO = Radius of footing

10. 10
STRESS UNDER UNIFORMLY LOADED
CIRCULAR AREA
Case-B: Vertical stress at any point in soil
z
a
RO
r
z
),( nmIq Zz 
where,
IZ = Shape function/ Influence factor
m = z/RO; n=r/RO
RO = Radius of footing
r = distance of Δσz from center of footing
z = depth of Δσz

11. 11
STRESS UNDER UNIFORMLY LOADED CIRCULAR AREA
(Foster & Alvin, 1954; U.S. Navy, 1986) Assumptions: Semi-infinite elastic
medium with Poisson’s ratio 0.5.
(stress in percent of surface contact pressure)

12. 12
A water tank is required to be constructed with a circular
foundation having a diameter of 16 m founded at a depth of 2 m
below the ground surface. The estimated distributed load on the
foundation is 325 kPa.
Assuming that the subsoil extends to a great depth and is
isotropic and homogeneous. Determine the stress z at points
(i) 10 m below NSL; at center of footing
(ii) 10 m below NSL; at distance of 8 m from central axis of footing
(iii) 18 m below NSL; at center of footing
(iv) 18 m below NSL; at distance of 8 m from central axis of footing
Neglect the effect of the depth of the foundation on the
stresses.
Practice Problem #7

13. 13
STRESS UNDER UNIFORMLY LOADED
RECTANGULAR AREA
Bousinesq equation can be extended for uniformly loaded
rectangular area as;
),( nmIq recz 
where,
IZ = Shape function/ Influence factor
m = b/z; n=l/z
x
z
q
A
y
z
dx
dy

14. 14
STRESS UNDER
UNIFORMLY
LOADED
RECTANGULAR
AREA
•14
z
L
n
z
B
m  ,
Log scale

15. 15
STRESS UNDER UNIFORMLY LOADED
RECTANGULAR AREA
This methods gives stress at the corner of rectangular area
),( nmIq recz 
A B
D C
Case I
E
F
G
A B
D C
Case II
σz due to ABCD =
4 x σz due to EBFG

16. 16
A 20 x 30 ft rectangular footing carrying a uniform load of 6000
lb/ft2 is applied to the ground surface.
Required
The vertical stress increment due to this uniform load at a depth
of 20 ft below the (i) corner, and (ii) center of loaded area.
G
A BE
D C
20 ft
30 ft
F
Practice Problem #8

17. 17
E
FH
G
E
FH
I
STRESS UNDER UNIFORMLY LOADED
RECTANGULAR AREA
G
A B
D C
A B
D C
I
A B
D C
Case I Case II
σz due to ABCD =
4 x σz due to EBFG
Case III
σz due to ABCD = σz due to
(EBFI + IFCG + IGDH + AEIH)

18. 18
E
I
STRESS UNDER UNIFORMLY LOADED
RECTANGULAR AREA
A B
D C
EF
GH
F
A B
D
C
Case IV
σz due to ABCD = 2 x σz due to ABEF
Case V
σz due to ABCD = 2 x σz due to EBCF
Case VI
σz due to ABCD = σz due to
(AEGI – BEGH – DFGI + CFGH)
A BE
D CF

19. 19
CONCLUDED
REFERENCE MATERIAL
An Introduction to Geotechnical Engineering (2nd Ed.)
Robert D. Holtz & William D. Kovacs
Chapter #10