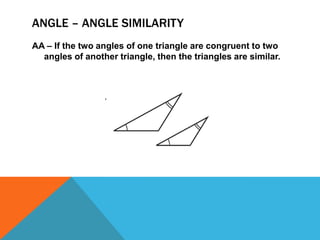
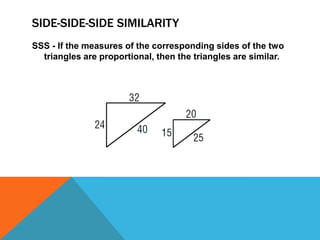
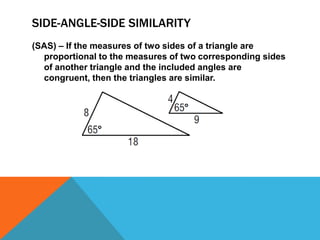
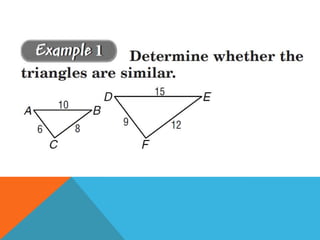
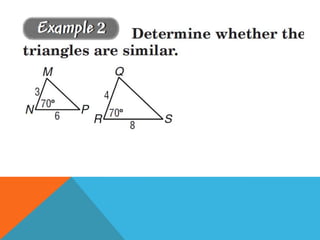
Similar triangles have congruent angles and proportional sides. There are three cases where triangles are similar: if two angles of one triangle are congruent to two angles of another (AA similarity), if the measures of corresponding sides are proportional (SSS similarity), or if two sides are proportional and the included angles are congruent (SAS similarity). Similarity of triangles follows the properties of being reflexive, symmetric, and transitive.

2. SIMILAR TRIANGLES
• How can I identify similar triangles and use
them to solve problems?

3. SIMILAR TRIANGLES
• Same rules as similar polygons
• Angles have to be congruent and corresponding sides
are proportional
• Special Cases so you don’t have to check every angle
and side

4. ANGLE – ANGLE SIMILARITY
AA – If the two angles of one triangle are congruent to two
angles of another triangle, then the triangles are similar.

5. SIDE-SIDE-SIDE SIMILARITY
SSS - If the measures of the corresponding sides of the two
triangles are proportional, then the triangles are similar.

6. SIDE-ANGLE-SIDE SIMILARITY
(SAS) – If the measures of two sides of a triangle are
proportional to the measures of two corresponding sides
of another triangle and the included angles are
congruent, then the triangles are similar.

7. SIMILARITY OF TRIANGLES
• Theorem 6.3
• Similarity of triangles is reflexive, symmetric and transitive.

10. ADDING ALGEBRA

11. HOMEWORK
• Page 302
#10 – 21
#32, 39