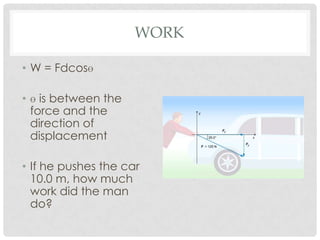
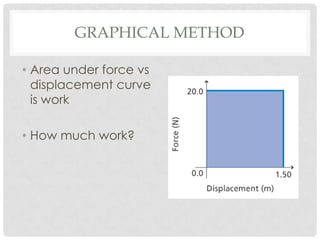
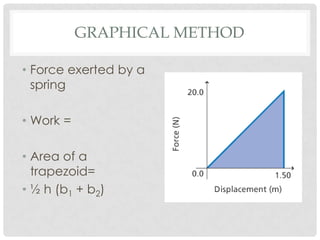
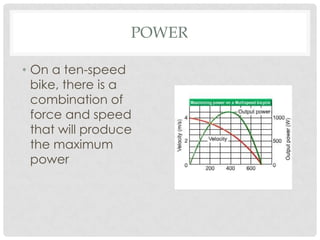
This document discusses energy, work, and simple machines. It defines work as the product of the applied force and the distance moved in the direction of the force. It provides the work equation as W=Fd, where W is work, F is force, and d is distance. The document also discusses how work is related to changes in kinetic energy through the work-energy theorem. Examples are provided to demonstrate calculating work done by forces applied at an angle to the direction of motion and work done against gravity.

1. ENERGY, WORK AND
SIMPLE MACHINES
CHAPTER 10

2. ENERGY AND WORK
• How do we define the relationship between work
and energy?
• How can we calculate work done?
• How do we calculate power used?

3. WORK EQUATION
•

4. WORK EQUATION
•

5. WORK EQUATION
• Right side is Fd
• F = force (in Newtons)
• d = distance (in meters)
• We define:
• W = Fd
• Work = forces times distance

6. WORK ENERGY THEOREM
•

7. EXAMPLE
• A 105 g hockey puck
is sliding across the
ice. A player exerts a
constant 4.50 newton
force over a distance
of 0.150 m. How
much work does the
player do on the
puck? What is the
change in energy?

8. LIFTING A BOOK
• When is the work positive?
• When is the work negative?
• When is the work zero?

9. WORK AGAINST GRAVITY
• W = Fd
• The work of lifting something is equal to the weight
of the object times the distance lifted
• Weight =
• So W =

10. WORK
• Since work equals the change in KE, the unit is the
same
• Work is measured in joules
• One joule happens when a force of 1 N acts for 1 m
• An apple is approximately a newton, so lifting an
apple 1 meter is about 1 Joule of work

11. WORK
• What if our force is not applied in a straight line?
• Will it be as effective?
• How do we account for this?

12. WORK
• W = Fdcosɵ
• ɵ is between the
force and the
direction of
displacement
• If he pushes the car
10.0 m, how much
work did the man
do?

13. WHAT TO INCLUDE IN WORK
• Which direction do
the normal force
and gravity point?
• ɵ is …
• What about
friction?

14. EXAMPLE
• A sailor pulls a boat
a distance of 30.0 m
along a dock using
a rope that makes
a 25.0° angle with
the horizontal. How
much work does
the sailor do on the
boat if he exerts a
force of 255 N on
the rope?

15. TRIG REFRESHER
• SOH-CAH-TOA

16. WORK AGAINST GRAVITY
• Pushing up a ramp,
walking up stairs
• What do we use for
d?

17. HOMEWORK
• Page 287, # 1 – 3
• Page 291, # 4 - 8

18. GRAPHICAL METHOD
• Area under force vs
displacement curve
is work
• How much work?

19. GRAPHICAL METHOD
• Force exerted by a
spring
• Work =
• Area of a
trapezoid=
• ½ h (b1 + b2)

20. MULTIPLE FORCES
• If several forces are exerted on a system, calculate
the work done by each force, then add the results

21. POWER
•

22. POWER
• Three student going
up stairs
• If they started at the
same time…
• How does their work
compare?
• How does their power
compare?

23. POWER
• On a ten-speed
bike, there is a
combination of
force and speed
that will produce
the maximum
power

24. EXAMPLE
• An electric motor lifts an elevator 9.00 m in 15.0 s by
exerting an upward force of 1.20 x 104 N. What
power does the motor produce in kW?

25. HOMEWORK
• Page 264, # 9 – 14
• Page 265, # 15 - 21