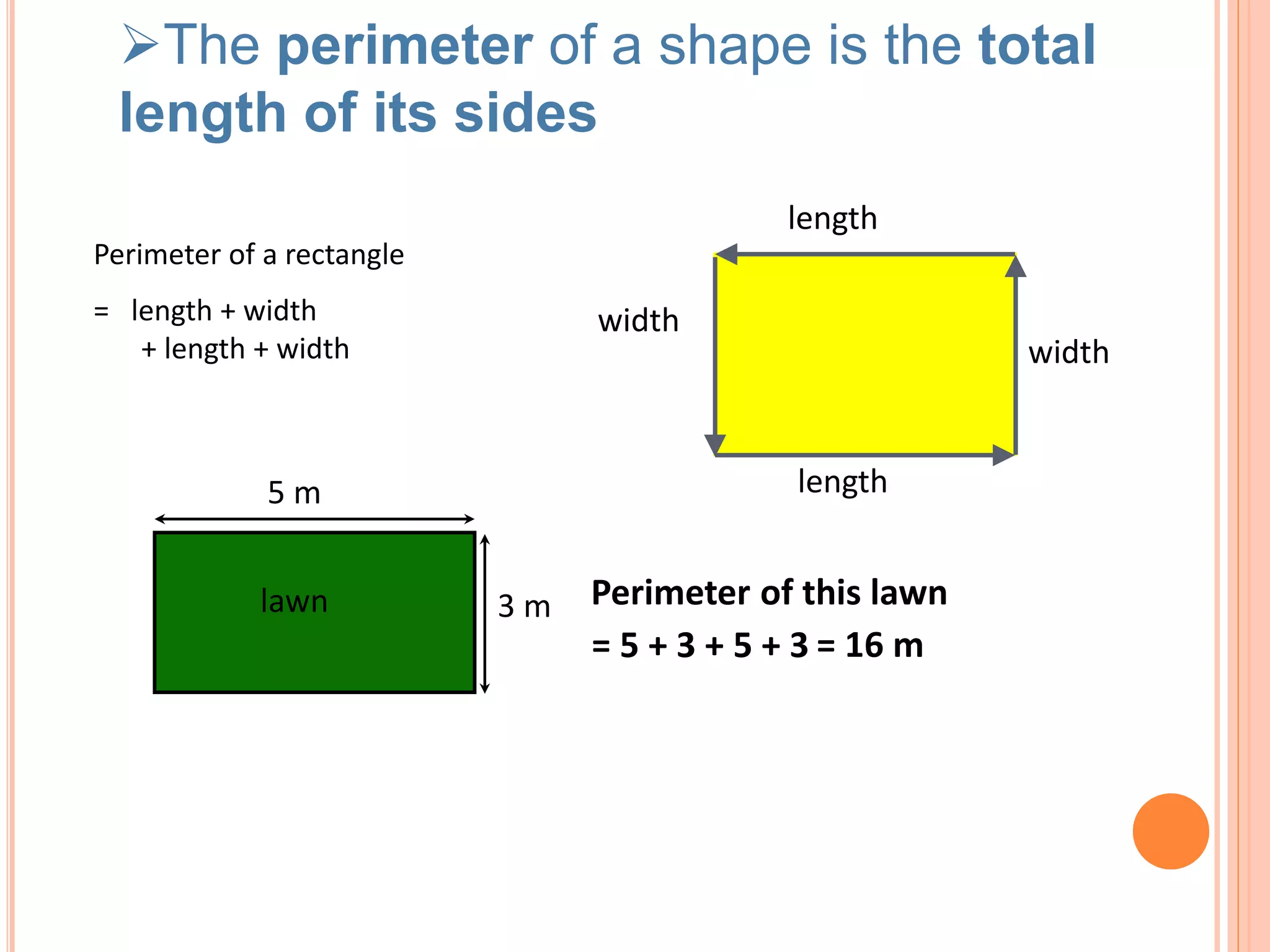
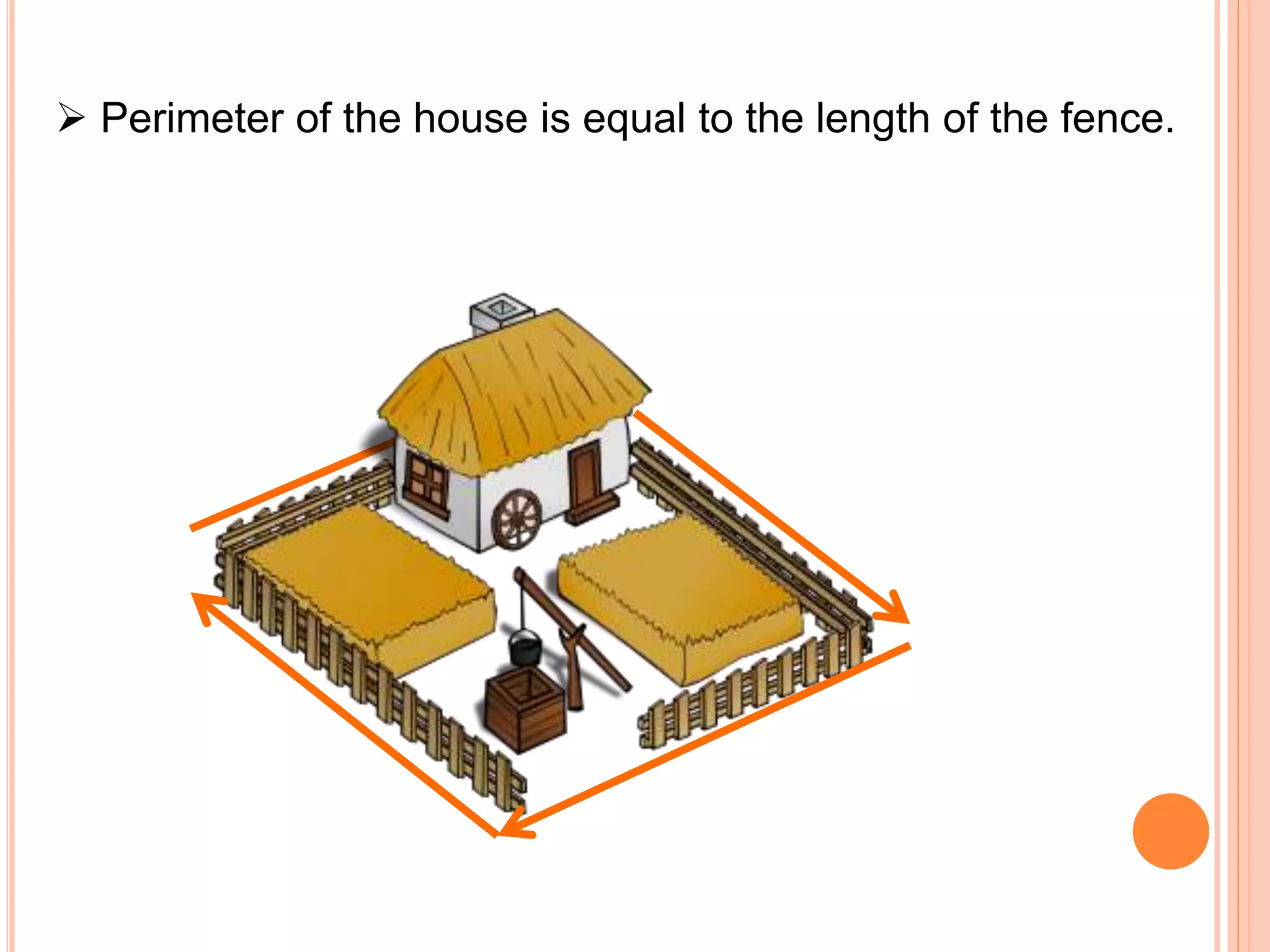
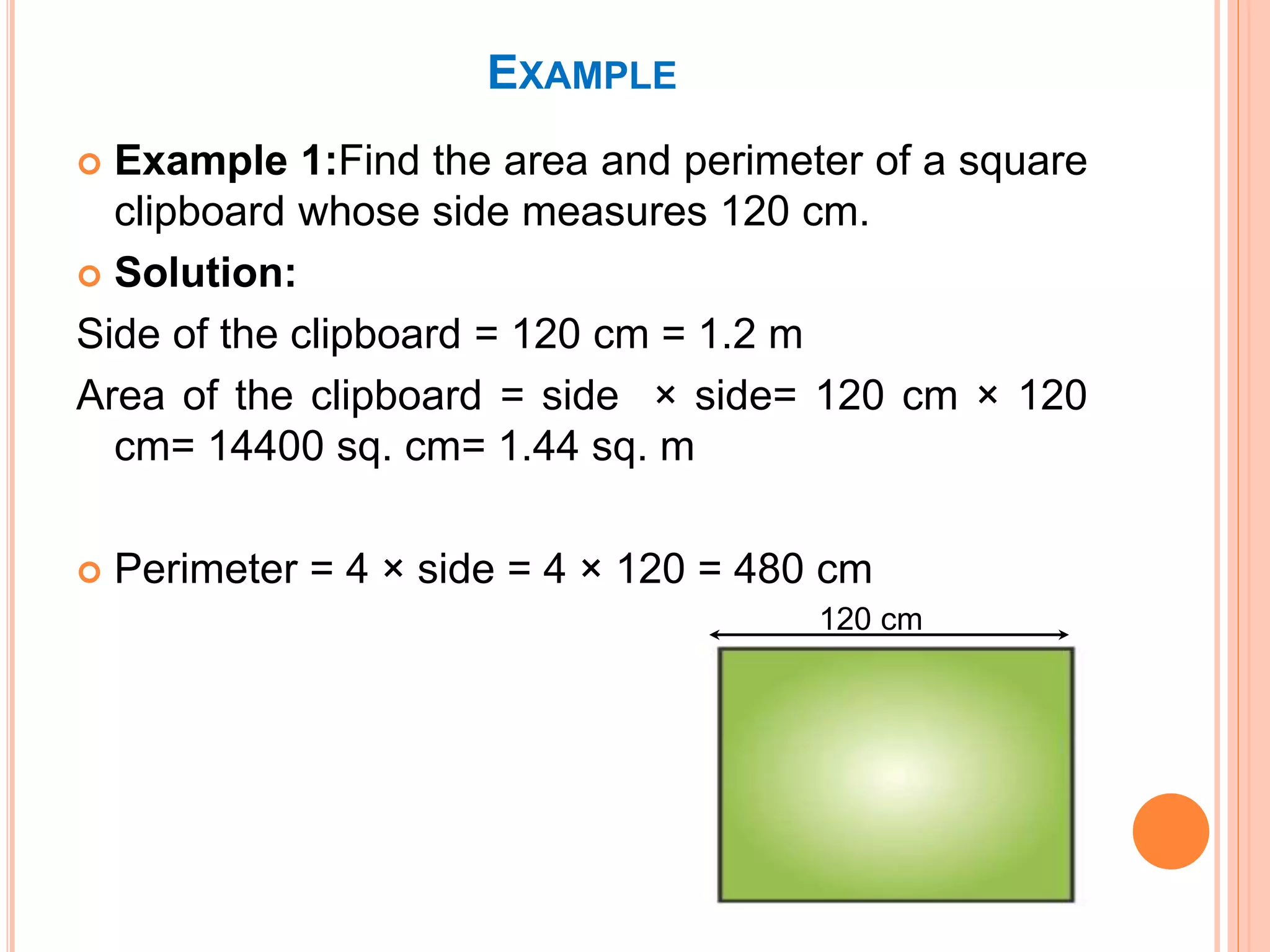
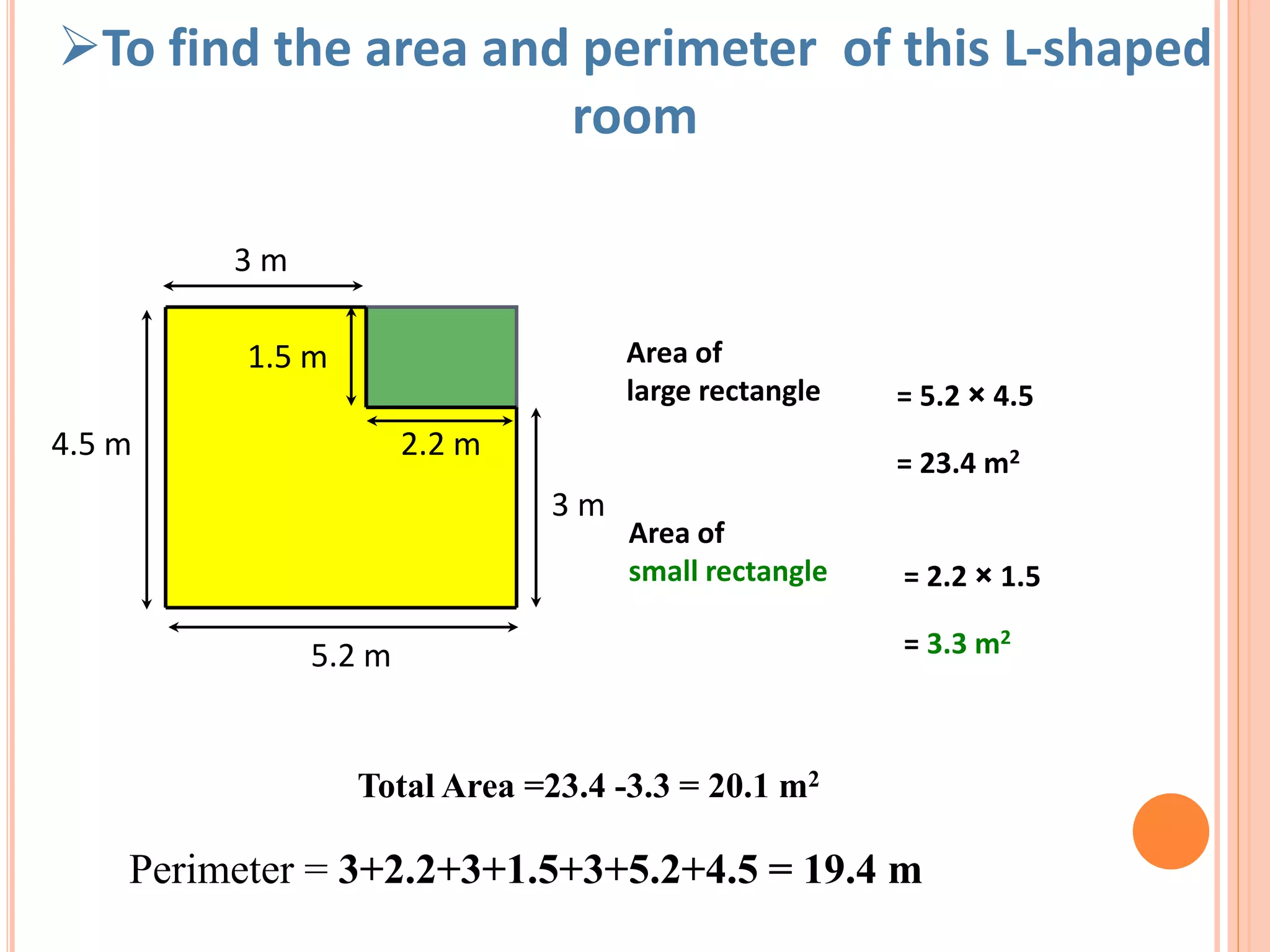
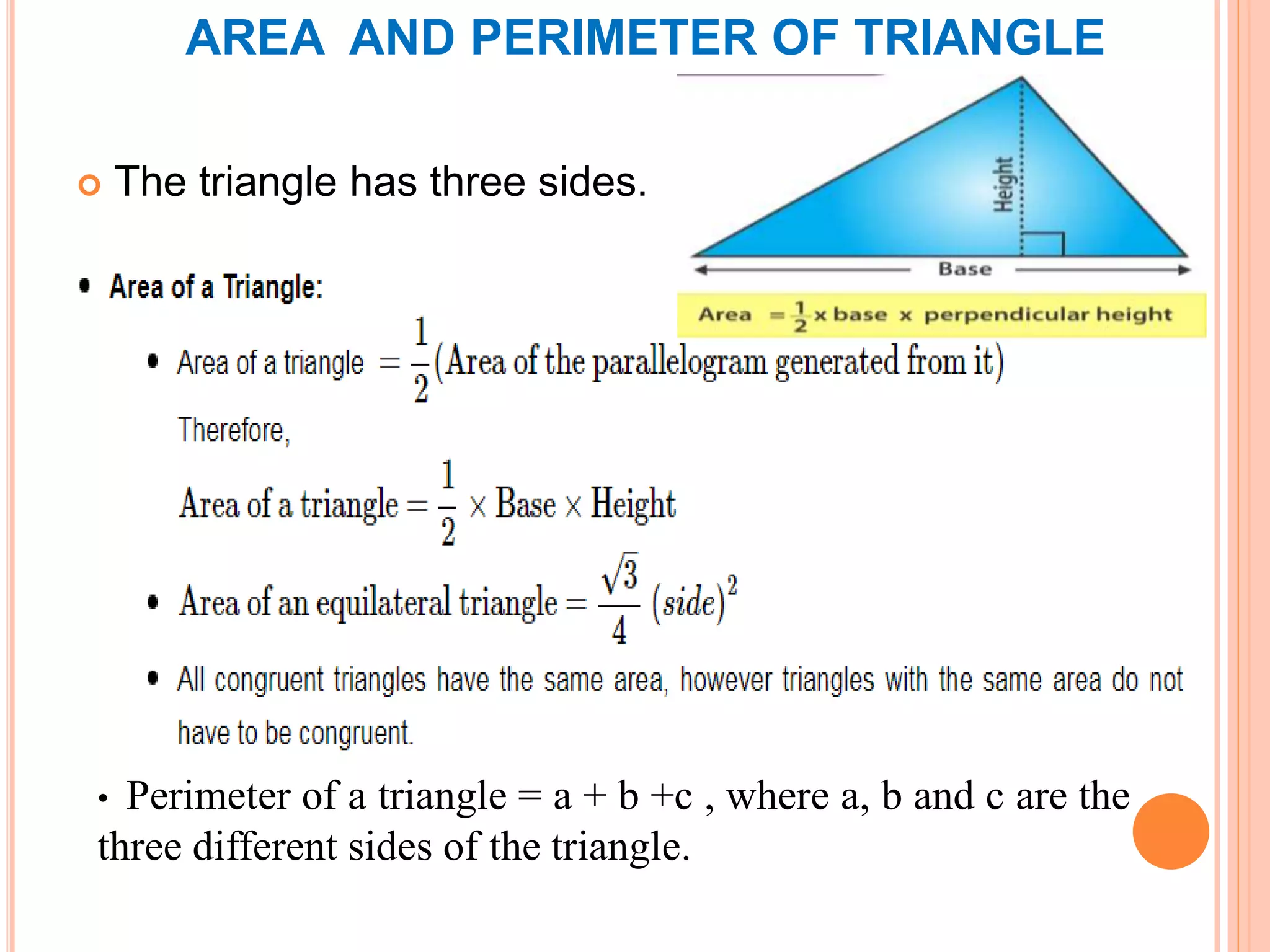
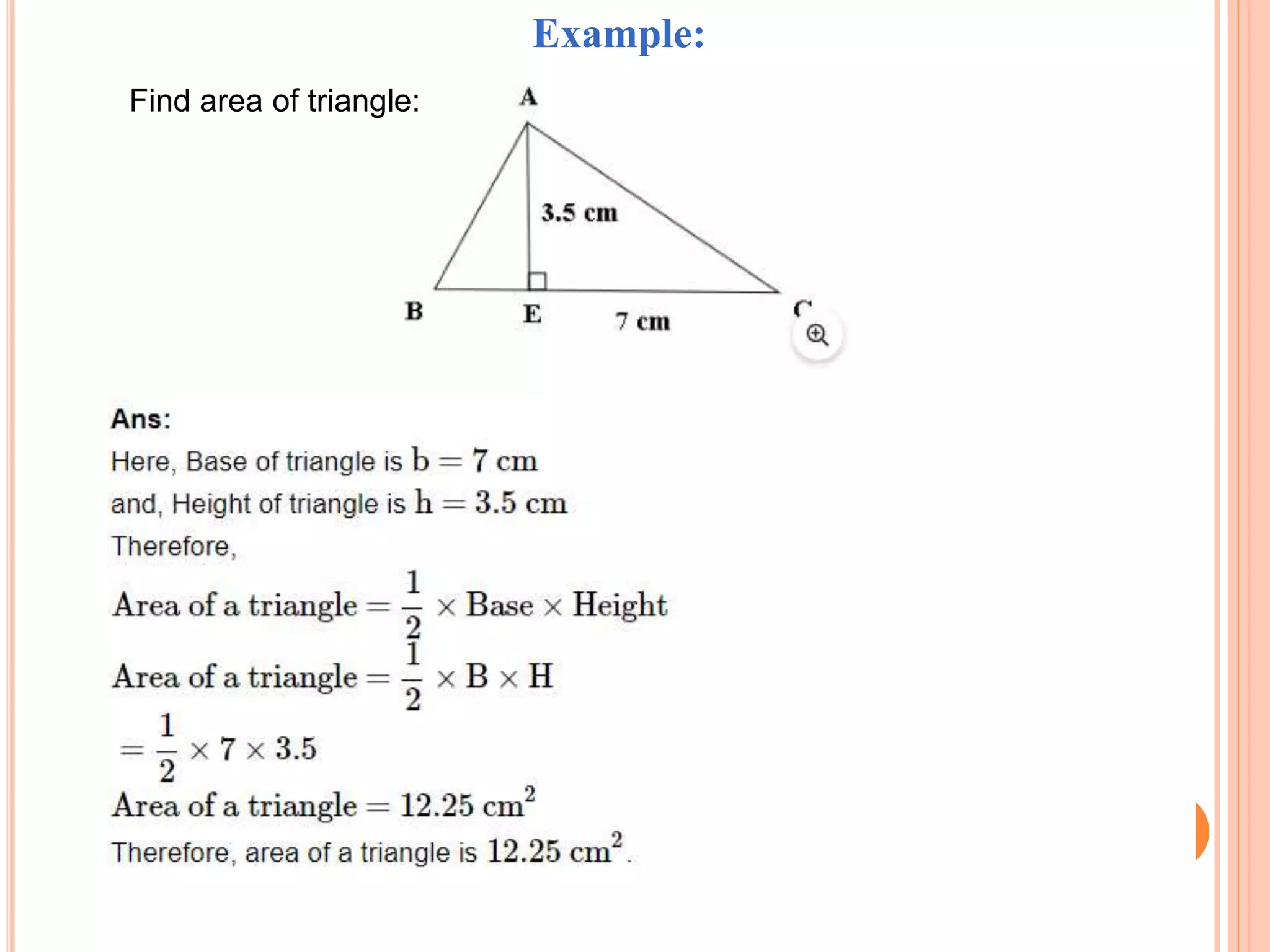
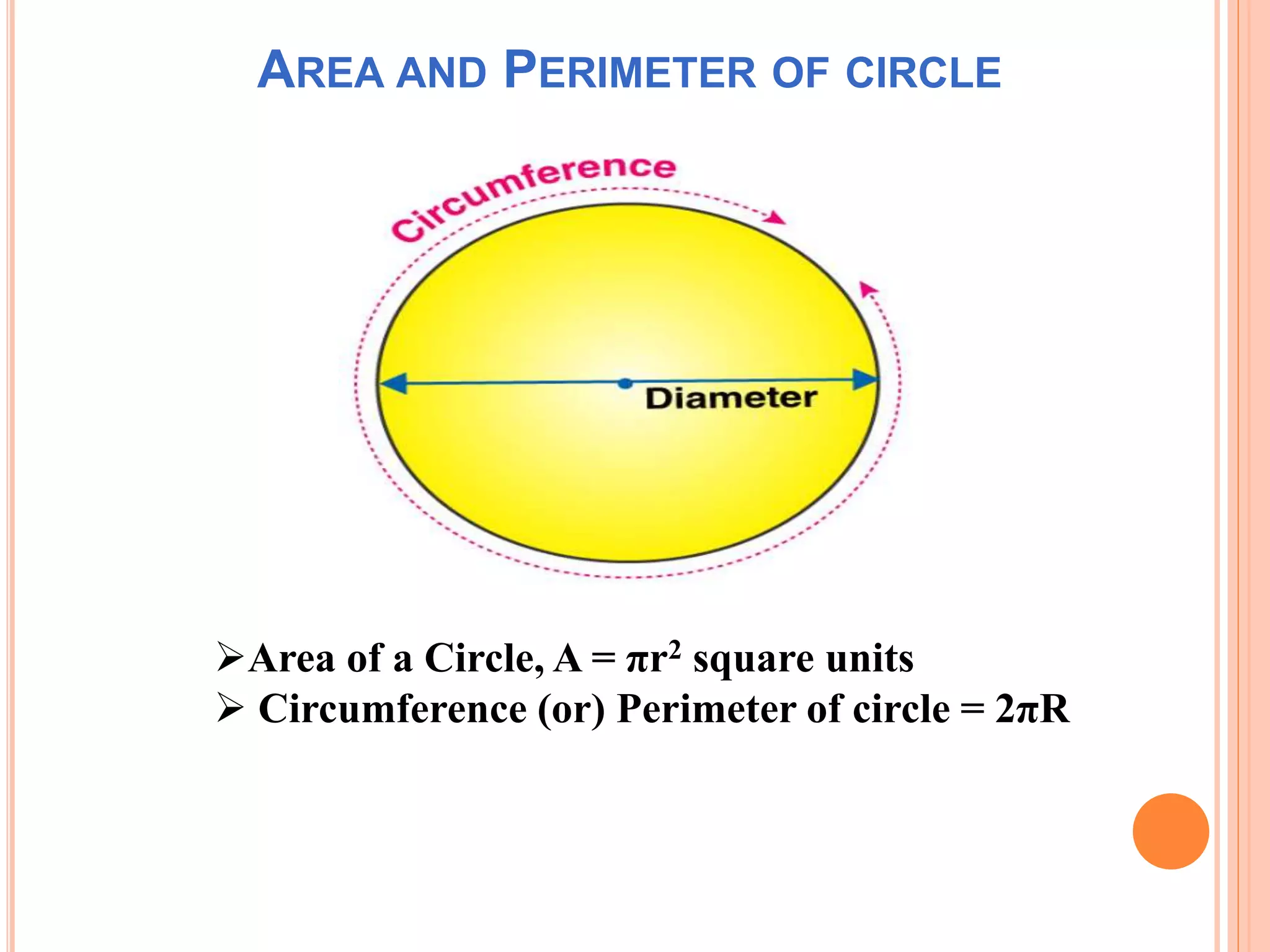
This document discusses the formulas for calculating the area and perimeter of various shapes. It defines area as the space within a shape and perimeter as the distance around the shape. Formulas are provided for calculating the area and perimeter of squares, rectangles, parallelograms, triangles, and circles. An example calculation is shown for each shape. The key concepts are that area is measured in square units and perimeter is measured in the same units as the shape's sides.

1. APEX INSTITUTE OF MGMT.
STUDIES AND RESEARCH
TOPIC:- AREA AND
PERIMETER
Presented By,
Roll No.:- E2209310017
B.Ed II Year
Session:- 2022-2023
Subject:- Mathematics

2. AREA
 Area is the region occupied by a shape.
 The space covered by the figure or any two-
dimensional geometric shape, in a plane, is the area of
the shape.
 The area of all the shapes depends upon their
dimensions and properties.
 Different shapes have different areas.
 Area is measured in square units (m2, cm2, in2, etc.)

3. PERIMETER
 Perimeter is total distance covered by the boundary
of a shape.
 A perimeter is a total distance that encompasses a
shape, in a 2d plane.
 Perimeter is measured in units (m, cm, in, feet, etc.)

4. Perimeter of a rectangle
length
width
length
width
= length + width
+ length + width
lawn
5 m
3 m
= 5 + 3 + 5 + 3
Perimeter of this lawn
= 16 m
The perimeter of a shape is the total
length of its sides

5.  Perimeter of the house is equal to the length of the fence.

6. SQUARE
 A Square is a figure/shape with all four sides equal and
all angles equal to 90 degrees.
 The area of the square is the space occupied by the
square in a 2D plane and its perimeter is the distance
covered on the outer line.

7. AREA AND PERIMETER OF SQUARE
 Perimeter of a Square = 4a units
 Area of a Square = a2 sq. units
 Where a is the side of Square

8. EXAMPLE
 Example 1:Find the area and perimeter of a square
clipboard whose side measures 120 cm.
 Solution:
Side of the clipboard = 120 cm = 1.2 m
Area of the clipboard = side × side= 120 cm × 120
cm= 14400 sq. cm= 1.44 sq. m
 Perimeter = 4 × side = 4 × 120 = 480 cm
120 cm

9. RECTANGLE
 A rectangle is a figure/shape with opposite sides
equal and all angles equal to 90 degrees.
 The area of the rectangle is the space covered by it
in an XY plane.

10. page
21 cm
30 cm
= 30 × 21
Area of the page = 630
65 m
32 m
= 65 × 32 m2
Area of field = 2080
cm2
field
AREA AND PERIMETER OF RECTANGLE
Perimeter of a Rectangle = 2(l+b)
Area of rectangle = length × width
Area of Rectangle = l × b

11. 5.2 m
4.5 m
3 m
3 m
1.5 m
2.2 m
Area of
large rectangle = 5.2 × 4.5
= 23.4 m2
Area of
small rectangle = 2.2 × 1.5
= 3.3 m2
Total Area =23.4 -3.3 = 20.1 m2
To find the area and perimeter of this L-shaped
room
Perimeter = 3+2.2+3+1.5+3+5.2+4.5 = 19.4 m

12. AREA AND PERIMETER OF A PARALLELOGRAM
 Any side of a parallelogram can be considered as the
base of the parallelogram.
 The perpendicular drawn on that side from the opposite
vertex is known as height (altitude).
 Area of a Parallelogram = Base × Height
 Perimeter = 2(Side + Base)

13. EXAM
Example :

14.  The triangle has three sides.
• Perimeter of a triangle = a + b +c , where a, b and c are the
three different sides of the triangle.
AREA AND PERIMETER OF TRIANGLE

15. Find area of triangle:
Example:

16. AREA AND PERIMETER OF CIRCLE
Area of a Circle, A = πr2 square units
 Circumference (or) Perimeter of circle = 2πR

17. EXAMPLE :
Question: Find the circumference and the area of
circle if the radius is 7 cm.
Solution: Given: Radius, r = 7 cm
 We know that the circumference/ perimeter of the circle
is 2πr cm.
 Now, substitute the radius value, we get
 C = 2 × (22/7)× 7 = 2×22 = 44 cm
 Thus, the circumference of the circle is 44 cm.
 Now, the area of the circle is πr2 cm2
 A = (22/7) × 7 × 7 = 22 × 7= 154 cm2