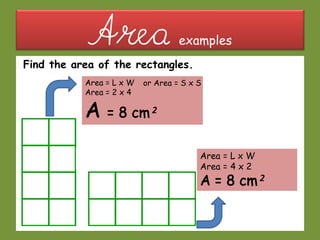
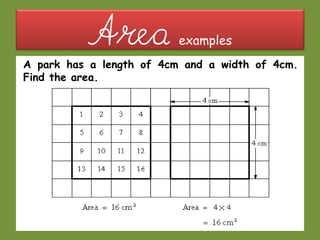
This document provides information about polygons, perimeter, and area. It defines a polygon as a 2D shape with straight sides. There are two types of polygons: regular and irregular. Perimeter is defined as the distance around a 2D shape and is measured by adding up the lengths of all sides. Area is the amount of surface a shape covers and is measured in square units. Formulas are provided to calculate the perimeter and area of common polygons like squares, rectangles, and triangles. Examples are given to demonstrate calculating perimeter and area using the appropriate formulas and units of measurement.

1. Mathematics
Perimeter and
Area of Polygons
Standard 3
Objectives

2. Polygons
• A polygon is a plane shape with straight sides.
Polygons are 2-dimensional shapes. They are made of
straight lines, and the shape is "closed" (all the lines
connect up).

3. Polygons
• Remember there are 2 types of polygons.

4. Non Regular Polygons
Other Common Polygons.
These are 2D shapes, and they are polygons, but not
regular polygons:

5. Not Polygons
Curved Shapes
These are also 2D shapes, but are not polygons because
they have curves:

6. Perimeter
The perimeter of a two-dimensional shape is the distance around the shape. You
can think of wrapping a string around a triangle. The length of this string would be
the perimeter of the triangle. Or walking around the outside of a park, you walk the
distance of the park’s perimeter.
Some people find it useful to think “Perimeter” because the edge of an object is its
rim and peRIMeter has the word “rim” in it.
rim

7. Perimeter
If the shape is a polygon, then you can add up all the lengths of the sides
to find the perimeter.
Be careful to make sure that all the lengths are measured in the same
units. You measure perimeter in linear units, which is one dimensional.
Examples of units of measure for length are inches, centimeters, or
feet.

8. Perimeter examples
Find the perimeter of the given regular polygon. All
measurements indicated are centimetres.
Perimeter = S +S + S +S
PeRIMeter = 3cm +3cm+ 3cm + 3cm.
P=12cm
Since all the sides are measured in
centimeter, just add the lengths of all
four sides to get the perimeter.
Remember to include units.

9. Perimeter examples
Find the perimeter of the given non-regular
polygon. All measurements indicated are
centimetres.
Perimeter = S +S + S +S
PeRIMeter = 5cm +3cm+ 5cm + 3cm.
P=16cm
Since all the sides are measured in
centimetres, just add the lengths of all
four sides to get the perimeter.
Remember to include units.

10. Perimeter examples
Find the perimeter of the given non-regular
polygon. All measurements indicated are inches.
Perimeter = S +S + S +S+ S +S.
PeRIMeter = 5 +3 + 6 + 2 + 3 + 3.
P = 22 inches
Since all the sides are measured in inches,
just add the lengths of all six sides to get
the perimeter.
Remember to include units.

11. Perimeter examples
Find the perimeter of the given non-regular
polygon. All measurements indicated are feet.
Perimeter = S +S + S +S
PeRIMeter = 8 +10 + 8 + 14.
P = 40 feet
Since all the sides are measured in feet,
just add the lengths of all four sides to
get the perimeter.
Remember to include units.

12. AreaThe area of a two-dimensional figure describes the amount of surface
the shape covers.
You measure area in square units of a fixed size.
Examples of square units of measure are square inches, square
centimeters, or square miles.
When finding the area of a polygon, you count how many squares of a
certain size will cover the region inside the polygon.

13. AreaYou can count that there are 16 squares, so the area is
16 square units. Counting out 16 squares doesn’t take too
long, but what about finding the area if this is a larger
square or the units are smaller? It could take a long
time to count.
Fortunately, you can use multiplication. Since there are 4 rows of 4
squares, you can multiply 4 • 4 to get 16 squares! And this can be
generalized to a formula for finding the area of a square with any
length, Area = s x s = s2.
You can write “in2” for square inches and “ft2” for
square feet.

14. AreaTo help you find the area of the many different
categories of polygons, mathematicians have developed
formulas. These formulas help you find the
measurement more quickly than by simply counting.
The formulas you are going to look at are all developed
from the understanding that you are counting the
number of square units inside the polygon. Let’s look at
a rectangle.

15. AreaYou can count the squares individually, but it is much easier to multiply 3
times 5 to find the number more quickly. And, more generally, the area
of any rectangle can be found by multiplying length times width.
Area = L x W = ______2.15 cm

16. Area examples
A rectangle has a length of 8 centimeters and a
width of 3 centimeters. Find the area.
You can count that there are 24 squares,
so the area is 24 square units.
Area = S x S or Area = L x W
Area = 8 x 3
There are 3 rows of 8 squares, you can
multiply 3 • 8 to get 24 squares.
Remember to include units.
It would take 24 squares, each measuring 1 cm
on a side, to cover this rectangle.

17. Area examples
A rectangle has a length of 12 centimeters and a
width of 2 centimeters. Find the area.
You can count that there are 24 squares, so the area is 24 square
units.
It would take 24 squares, each measuring 1 cm on a side, to cover this rectangle.

18. Area examples
Find the area of the rectangles.
Area = L x W
Area = 4 x 2
Area = L x W
Area = 2 x 4
or Area = S x S

19. Area examples
A park has a length of 4cm and a width of 4cm.
Find the area.