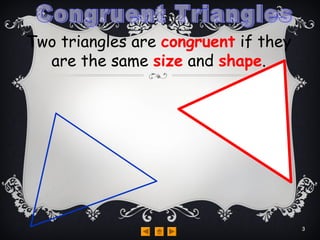
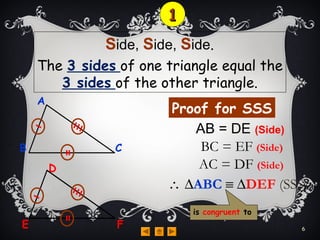
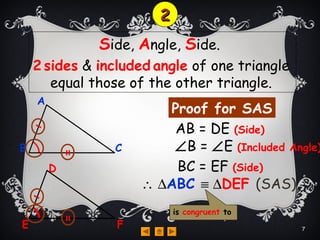
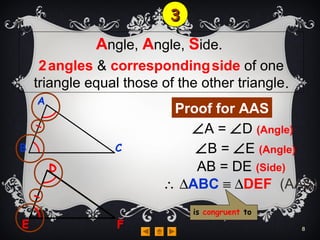
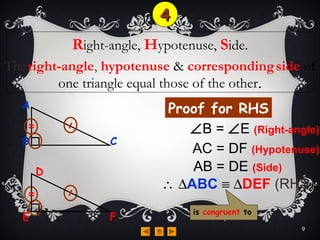
Triangles are congruent if they have the same size and shape. There are four rules to determine if triangles are congruent: side-side-side, side-angle-side, angle-angle-side, and right-angle-hypotenuse-side. The rules state that if two triangles have either three matching sides, two matching sides and the angle between them, two matching angles and a matching side, or a right angle, matching hypotenuse, and matching side, then the triangles are congruent.

1. ongruent triangles have congruent sides and congruent angles.
he parts of congruent triangles that “match” are called
corresponding parts.
1

2. 2

3. They
are
congruent
Two triangles are congruent if they
are the same size and shape.
3

4. They
arenot
congruent
Two triangles are not congruent if
they are not the same size
and shape.
4

5. Two triangles are congruent if they
are the same size and shape.
There are four Rules
Side, Side, Side.
Side, Angle, Side.
Angle, Angle, Side.
Right Angle, Hypotenuse, Side.
5

6. 11
Side, Side, Side.
The 3 sides of one triangle equal the
3 sides of the other triangle.
A
B C
D
E F
Proof for SSS
AB = DE (Side)
BC = EF (Side)
AC = DF (Side)D
E F
∴ ∆ABC ≡ ∆DEF (SSS)
is congruent to
6

7. 22
Side, Angle, Side.
2 sides & included angle of one triangle
equal those of the other triangle.
A
B C
D
E F
Proof for SAS
AB = DE (Side)
BC = EF (Side)
∠B = ∠E (Included Angle)
D
E F
∴ ∆ABC ≡ ∆DEF (SAS)
is congruent to
7

8. 33
Angle, Angle, Side.
2angles & correspondingside of one
triangle equal those of the other triangle.
A
B C
D
E F
Proof for AAS
∠A = ∠D (Angle)
AB = DE (Side)
∠B = ∠E (Angle)
D
E F
∴ ∆ABC ≡ ∆DEF (AAS)
is congruent to
8

9. 44
Right-angle, Hypotenuse, Side.
Theright-angle, hypotenuse & correspondingside of
one triangle equal those of the other.
Proof for RHS
∠B = ∠E (Right-angle)
AB = DE (Side)
AC = DF (Hypotenuse)
A
B C
D
E F
D
E F
∴ ∆ABC ≡ ∆DEF (RHS)
is congruent to
9

10. 10
THANK YOU
EFFORTS BY :
VANSHIKA DORA
PARINEETA VERMA
SULAGNA MISHRA
GHANISHTHA GOSWAMI
SHRUTI MATHUR
CLASS 9-A