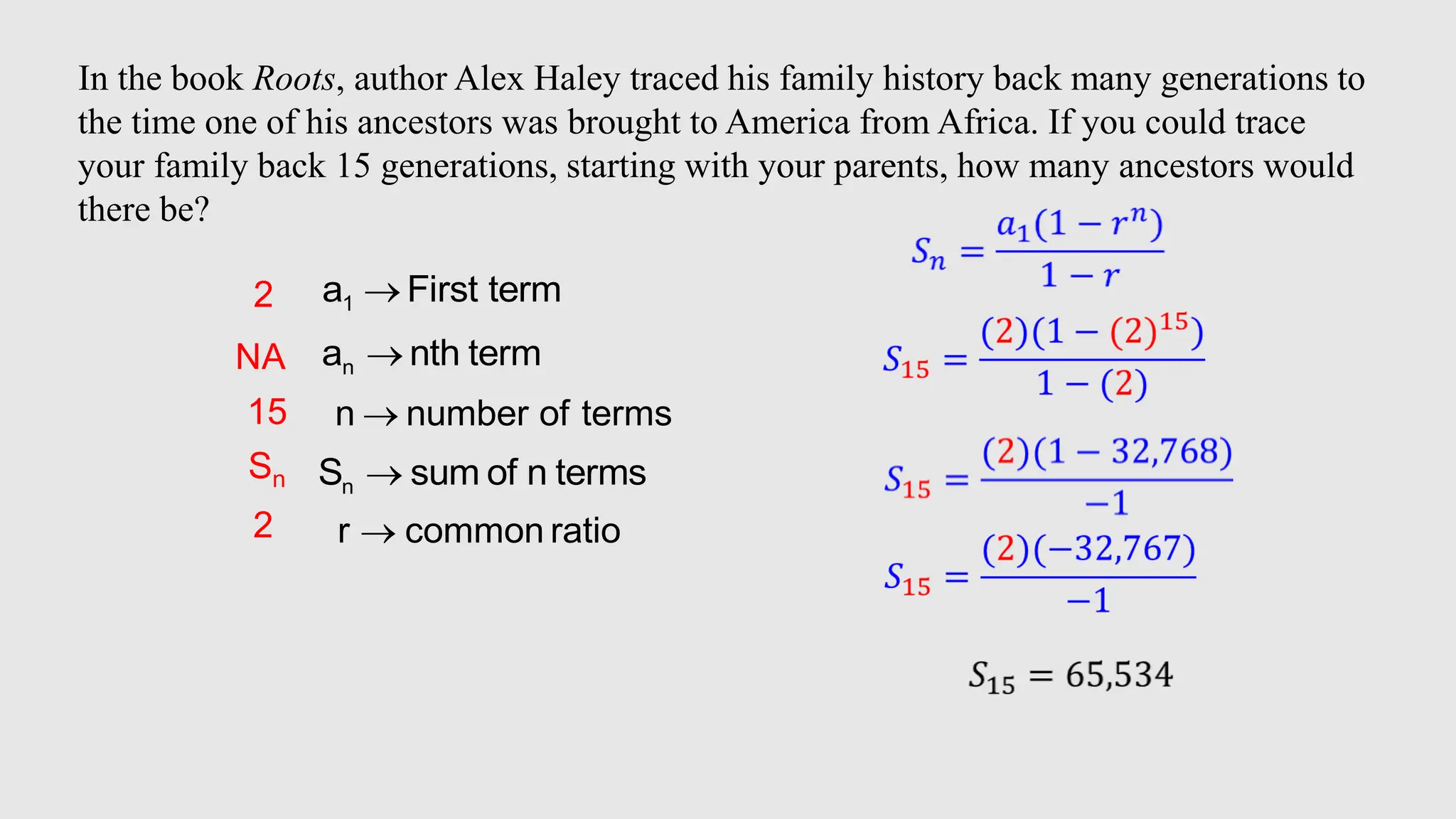The document discusses geometric and arithmetic sequences and series, emphasizing the differences in how terms are generated: geometric sequences use multiplication by a common ratio while arithmetic sequences rely on addition. It includes examples of finding the next terms in sequences and calculating sums, as well as definitions of key terms like first term, nth term, sum of terms, and common ratio. Additionally, it touches on geometric means and properties of exponents.

1. Geometric Sequences and Series

2. 1, 4, 7,10,13
9,1, 7, 15
6.2, 6.6, 7, 7.4
, 3, 6
 
    
Arithmetic Sequences
ADD
To get next term
2, 4, 8,16, 32
9, 3,1, 1/3
1,1/ 4,1/16,1/ 64
, 2.5 , 6.25
 
  
Geometric Sequences
MULTIPLY
To get next term
Arithmetic Series
Sum of Terms
35
12
27.2
3 9

 
Geometric Series
Sum of Terms
62
20/3
85/ 64
9.75

3. • Geometric Sequence: sequence whose consecutive
terms have a common ratio.
• Example: 3, 6, 12, 24, 48, ...
• The terms have a common ratio of 2.
• The common ratio is the number r.
• To find the common ratio you use an+1 ÷ an

4. Vocabulary of Sequences (Universal)
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

r common ratio


5. Find the next two terms of 2, 6, 18, ___, ___
6 – 2 vs. 18 – 6… not arithmetic
2, 6, 18, 54, 162
Find the next two terms of 80, 40, 20, ___, ___
40 – 80 vs. 20 – 40… not arithmetic
80, 40, 20, 10, 5

6. Find the next three terms of 2, 3, 9/2, ___, ___, ___
3 – 2 vs. 9/2 – 3… not arithmetic
3 9/ 2 3
1.5 geometric r
2 3 2
    
9
2, 3, , ,
27 81 243
4 8
,
2 16
Find the next two terms of -15, 30, -60, ___, ___
30 – -15 vs. -60 – 30… not arithmetic
-15, 30, -60, 120, -240

7. 1
a First term

n
a nth term

n
S sum of n terms

n number of terms

r common ratio

-3
an
8
NA
-2
n 1
n 1
a a r 

Find the 8th term if a1 = -3 and r = -2.

8. 1
a First term

n
a nth term

n
S sum of n terms

n number of terms

r common ratio

??
an
10
NA
3
n 1
n 1
a a r 

Find the 10th term if a4 = 108 and r = 3.
4

9. Write an equation for the nth term of the geometric
sequence 3, 12, 48, 192, …
3
4
1
a First term

r common ratio

n 1
n 1
a a r 


10. Geometric Mean: The terms between any two
nonconsecutive terms of a geometric sequence.
Ex. 2, 6, 18, 54, 162
6, 18, 54 are the Geometric Mean between 2 and 162

11. Find two geometric means between –2 and 54
-2, ____, ____, 54
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

r common ratio

-2
54
4
NA
r
n 1
n 1
a a r 

The two geometric means are 6 and -18, since –2, 6, -18, 54
forms a geometric sequence

12. Geometric Series: An indicated sum of terms in a
geometric sequence.
Example:
Geometric Sequence
3, 6, 12, 24, 48
VS Geometric Series
3 + 6 + 12 + 24 + 48

13. Recall
Vocabulary of Sequences (Universal)
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

r common ratio


14. 1
a First term

n
a nth term

n
S sum of n terms

n number of terms

r common ratio

3
10
Sn
NA
Find the sum of the first 10 terms of the geometric series 3 - 6 + 12 – 24+ …
-2

15. In the book Roots, author Alex Haley traced his family history back many generations to
the time one of his ancestors was brought to America from Africa. If you could trace
your family back 15 generations, starting with your parents, how many ancestors would
there be?
1
a First term

n
a nth term

n
S sum of n terms

n number of terms

r common ratio

2
15
Sn
NA
2

16. 1
a First term

n
a nth term

n
S sum of n terms

n number of terms

r common ratio

a1
8
39,360
NA
3

17. 1
a First term

n
a nth term

n
S sum of n terms

n number of terms

r common ratio

15,625
??
Sn
-5

18. Recall the properties of exponents. When multiplying like bases add exponents

19. 1
a First term

n
a nth term

n
S sum of n terms

n number of terms

r common ratio

15,625
??
Sn
-5