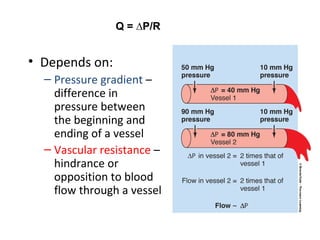
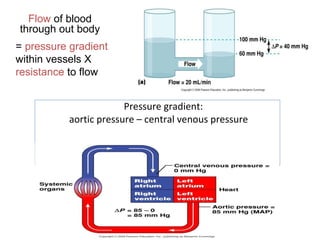
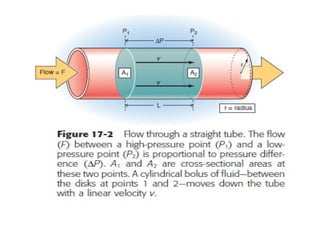
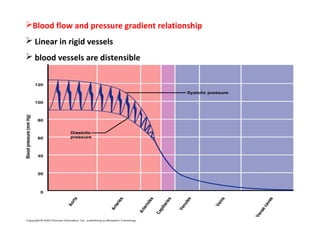
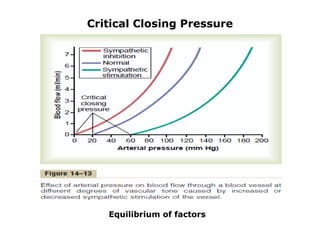
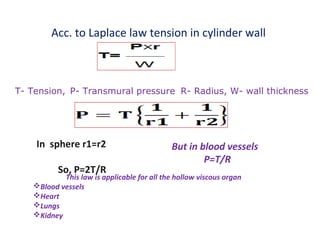
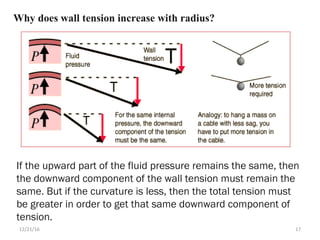
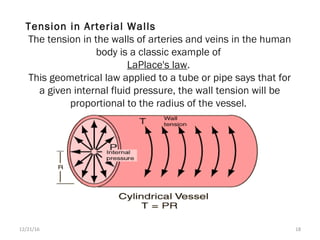
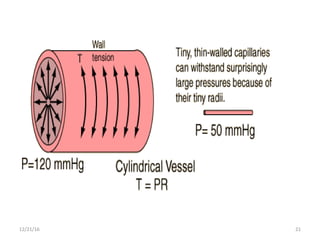
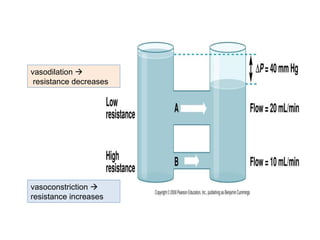
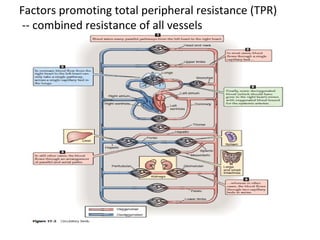
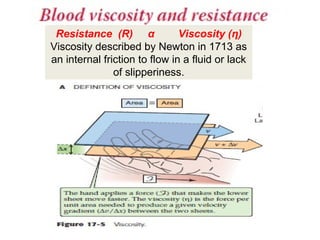
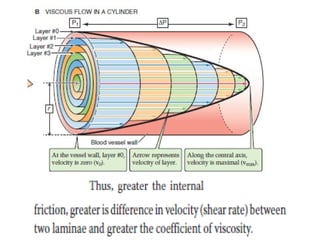
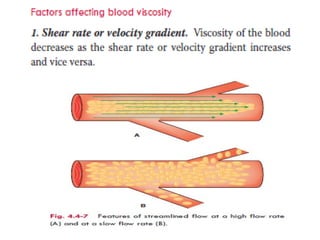
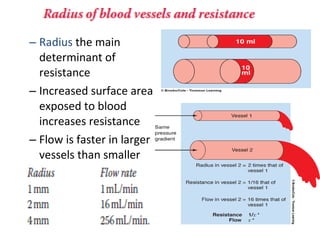
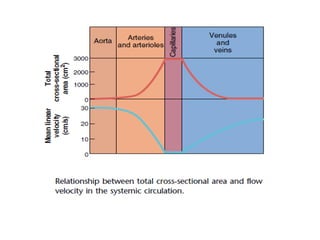
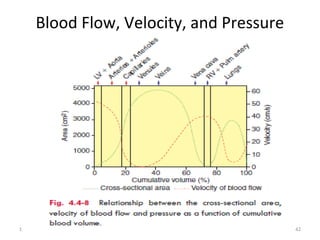
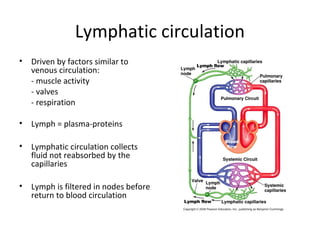
Blood flow is dependent on the pressure gradient between two points in the circulatory system and the resistance to flow within the vessels. The pressure gradient is determined by the difference in pressure between the beginning and end of a vessel and governs blood flow. Resistance depends on factors like vessel diameter, length, and viscosity and opposes blood flow. Larger arteries have less resistance but require stronger walls to withstand higher pressures due to Laplace's law. Capillaries have high resistance due to their small diameter but require only thin walls. Resistance increases as vessel diameter decreases. Blood velocity is directly related to vessel cross-sectional area and inversely related to resistance.

1. General principals of
circulation
Contin……..

2. 1-Blood flow
 Relationship with Pressure gradient
 Relationship with Resistance
2-velocity of blood
 Relationship with Cross sectional area
 Relationship with Pressure

3. Q = ∆P/R
• Depends on:
– Pressure gradient –
difference in
pressure between
the beginning and
ending of a vessel
– Vascular resistance –
hindrance or
opposition to blood
flow through a vessel

4. Blood flow and pressure gradient
relationship

5. Pressure gradient:
aortic pressure – central venous pressure
Flow of blood
through out body
= pressure gradient
within vessels X
resistance to flow

6. In hemodynamic,
difference in two Pressure is compared
PB and pressure inside blood vessels
Pressure difference b/w two points separated
by some distance
So, pressure gradient is expressed as
= F/A
= ∆P/ ∆x

8. Considering this we can define three different
kinds of pressure differences in the circulation-
1-Driving pressure
-axial pressure difference,
2-Transmural pressure-
Radial pressure difference
3- Hydrostatic pressure
-

9. 1-Driving pressure-
axial pressure difference, In Circulation it is arterial and
venous end pressure difference, in systemic or pulmonary
circulation
It governs the flow of blood
2-Transmural pressure-
Radial axis pressure difference
It is pressure difference b/w intravascular and tissue
pressure
It governs vessel diameter and major determinate of
resistance
3- Hydrostatic pressure-
density of blood and gravitational force when blood lies
in vertical column

11. Blood flow and pressure gradient relationship
 Linear in rigid vessels
 blood vessels are distensible

12. Critical Closing Pressure
Equilibrium of factors

13. Critical Closing Pressure
1 - vasomotor tone
2 - Intramural pressure
These factors equilibrate and maintain
the blood flow
Can be understand by a physics law
called as Laplace Law

14. Pascal's principle states that the pressure is everywhere
same inside the balloon at equilibrium.
But examination immediately reveals that there are great
differences in wall tension on different parts of the balloon. The
variation is described by Laplace's Law.

15. Acc. to Laplace law tension in cylinder wall
T- Tension, P- Transmural pressure R- Radius, W- wall thickness
In sphere r1=r2
So, P=2T/R
But in blood vessels
P=T/R
This law is applicable for all the hollow viscous organ
Blood vessels
Heart
Lungs
Kidney

16. LaPlace's Law
The larger the vessel radius, the larger the wall tension
required to withstand a given internal fluid pressure.
For a given vessel radius and internal pressure, a
spherical vessel will have half the wall tension of a
cylindrical vessel.
Why does the wall tension increase with radius?
12/21/16 16

17. Why does wall tension increase with radius?
If the upward part of the fluid pressure remains the same, then
the downward component of the wall tension must remain the
same. But if the curvature is less, then the total tension must
be greater in order to get that same downward component of
tension.
12/21/16 17

18. Tension in Arterial Walls
The tension in the walls of arteries and veins in the human
body is a classic example of
LaPlace's law.
This geometrical law applied to a tube or pipe says that for
a given internal fluid pressure, the wall tension will be
proportional to the radius of the vessel.
12/21/16 18

19. The implication of this law for the large arteries,
which have comparable blood pressures, is that the
larger arteries must have stronger walls since an
artery of twice the radius must be able to withstand
twice the wall tension.
Arteries are reinforced by fibrous bands to
strengthen them against the risks of an aneurysm.
The tiny capillaries rely on their small size.

20. The walls of the capillaries of the human circulatory system
are so thin as to appear transparent under a microscope,
yet they withstand a pressure up to about half of the full
blood pressure.
LaPlace's law gives insight into how they are able to
withstand such pressures: their small size implies that the
wall tension for a given internal pressure is much smaller
than that of the larger arteries.
12/21/16 20
Capillary Walls

21. 12/21/16 21

22. Blood flow and resistance
relationship

23. The larger arteries provide much less resistance
to flow than the smaller vessels according to
Poiseuille's law, and thus the drop in pressure
across them is only about half the total drop.
The capillaries offer large resistances to flow,
but don’t required much strength in their walls

24. According mathematical calculation in
Principles of physics, Resistance is
represented as -
R = 8ηl/∏r4
After replacing these values in Poiseuille’s law
by R
Blood flow Q will be
Q = ∆P/R

25. In vascular system, resistance to flow is represented
by the total peripheral resistance and is expressed as
peripheral resistance unit

27. vasodilation 
resistance decreases
vasoconstriction 
resistance increases

28. Factors promoting total peripheral resistance (TPR)
-- combined resistance of all vessels

29. – As resistance increases flow rate decreases

30. Resistance (R) α Viscosity (η)
Viscosity described by Newton in 1713 as
an internal friction to flow in a fluid or lack
of slipperiness.

36. – Radius the main
determinant of
resistance
– Increased surface area
exposed to blood
increases resistance
– Flow is faster in larger
vessels than smaller

37. • Vascular resistance  opposition to blood flow due to friction
between blood and the walls of blood vessels
– Increase in vascular resistance = increase in BP
– Decrease in vascular resistance = decease in BP
• Vascular resistance is dependent upon:
– Size of the blood vessel (lumen)
• Smaller means greater resistance to blood flow; alternates
between vasoconstriction and vasodilation
– Blood viscosity
• Ratio of RBCs to plasma volume
• Higher viscosity = higher resistance
– Total blood vessel length
• Resistance increase with total length
• Longer the length = greater contact between vessel wall and
blood

38. 2-velocity of blood
 Relationship with Cross sectional area
 Relationship with Pressure

39. 12/21/16 39

40. Relationship with Cross sectional area

42. Blood Flow, Velocity, and Pressure
12/21/16 42

43. Lymphatic circulation
• Driven by factors similar to
venous circulation:
- muscle activity
- valves
- respiration
• Lymph = plasma-proteins
• Lymphatic circulation collects
fluid not reabsorbed by the
capillaries
• Lymph is filtered in nodes before
return to blood circulation