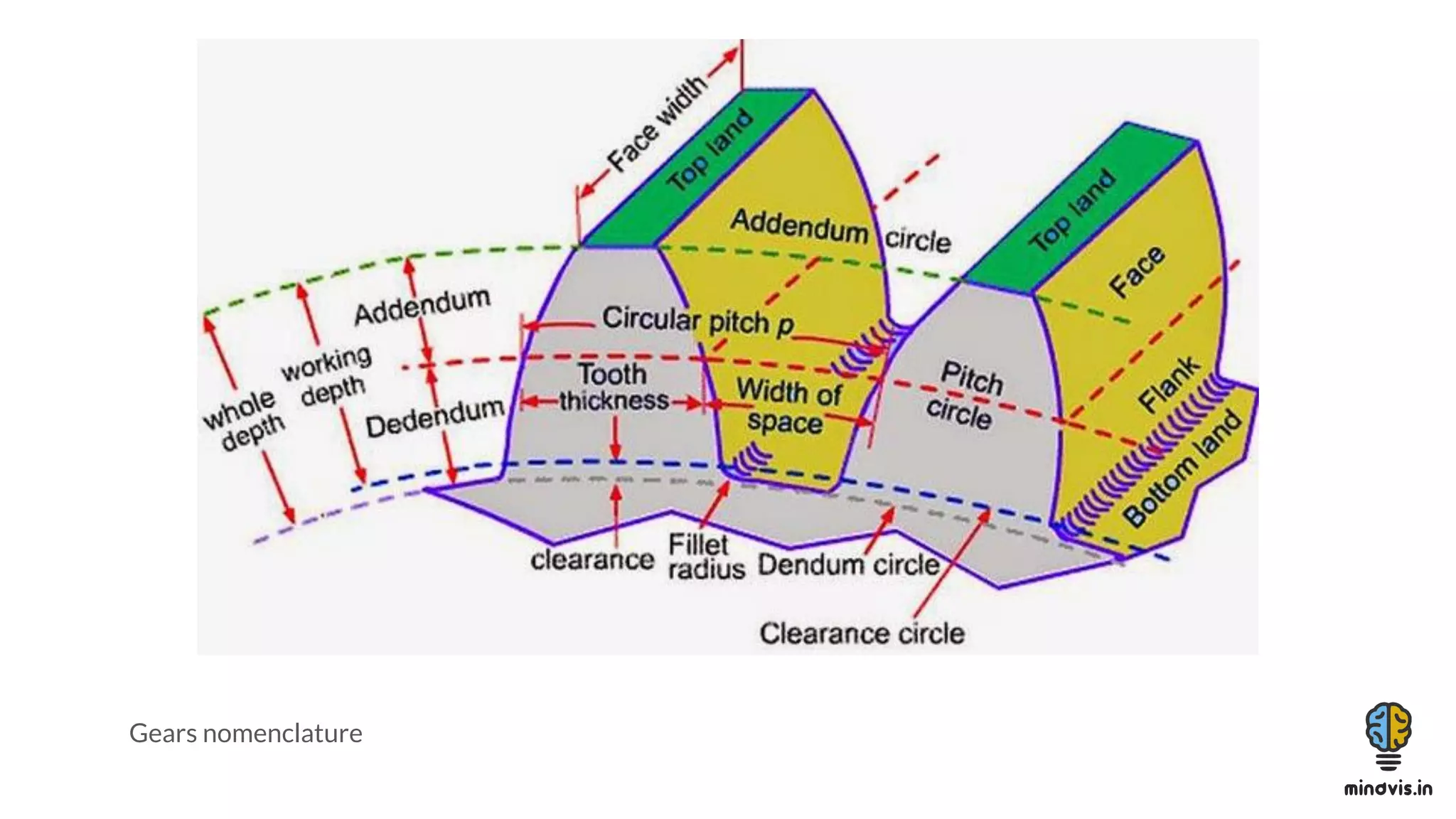
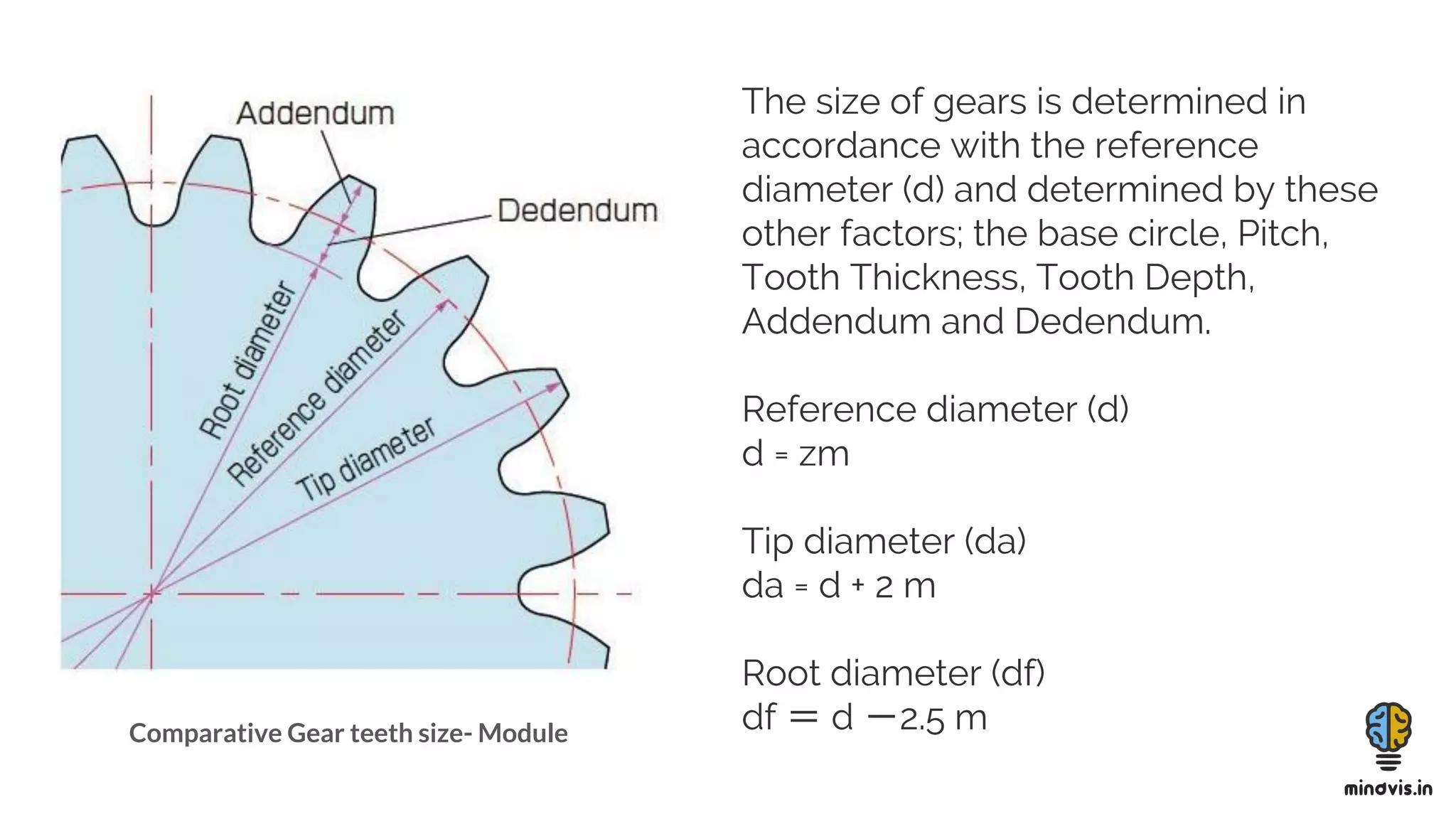
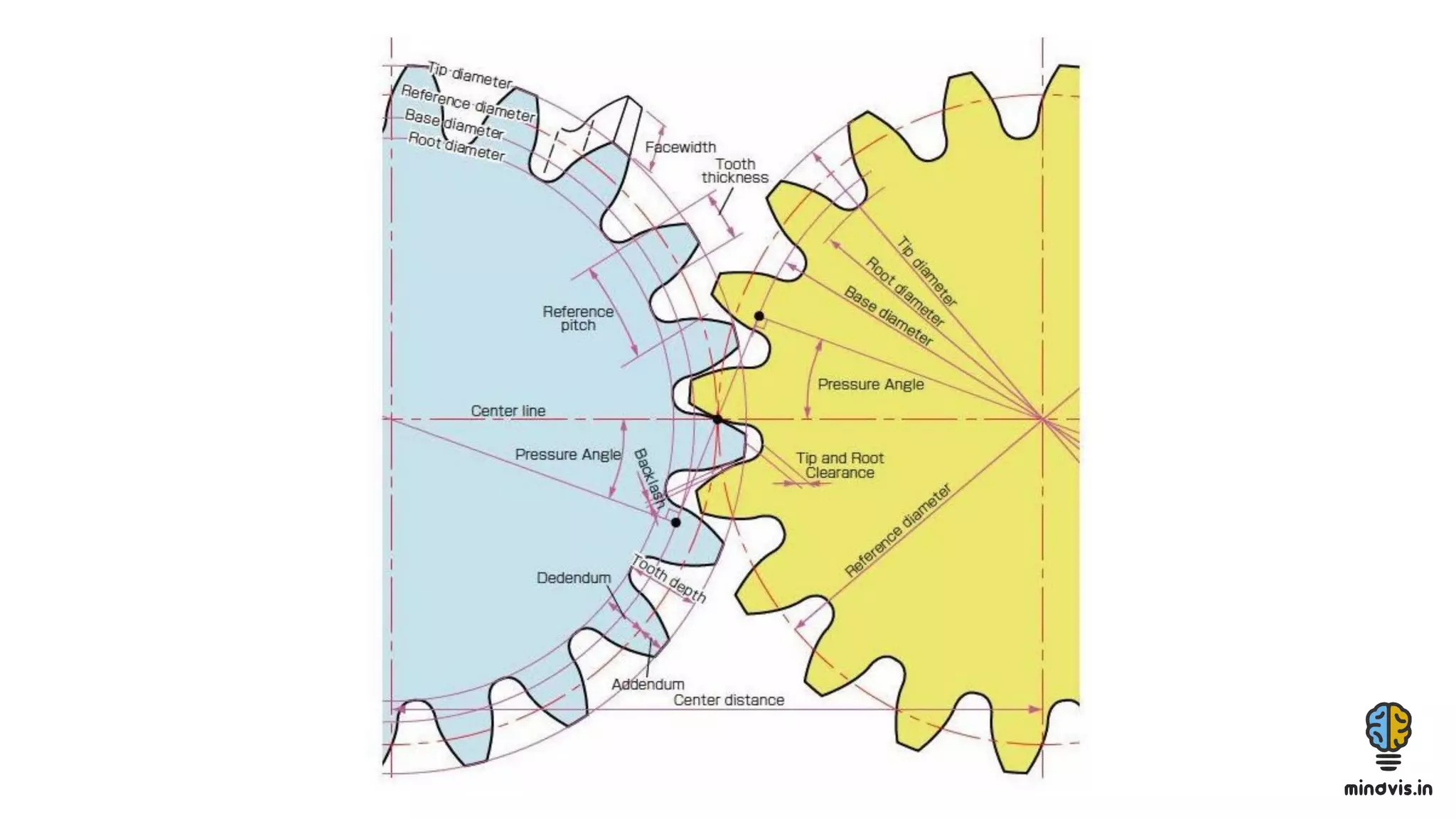
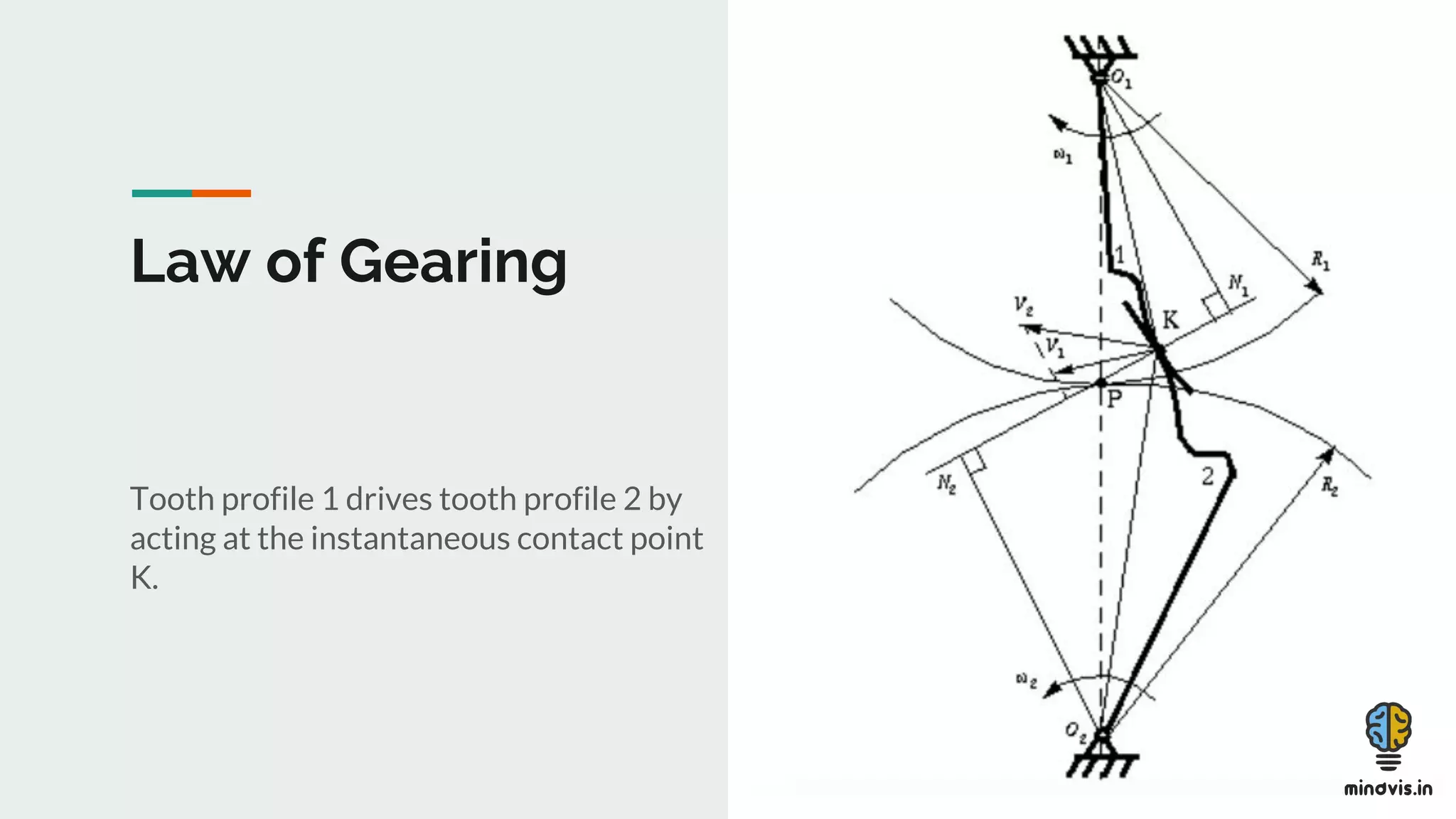
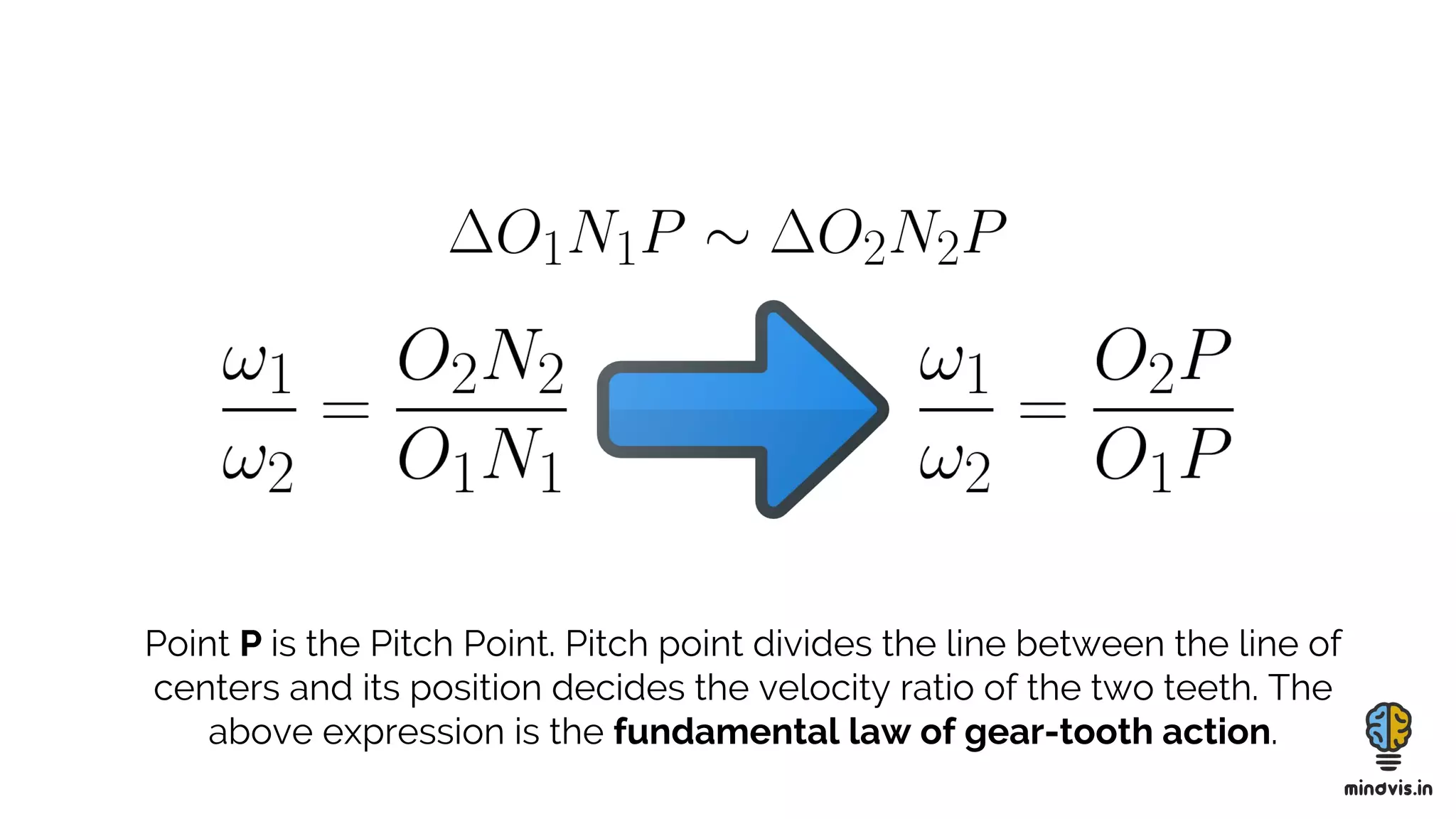
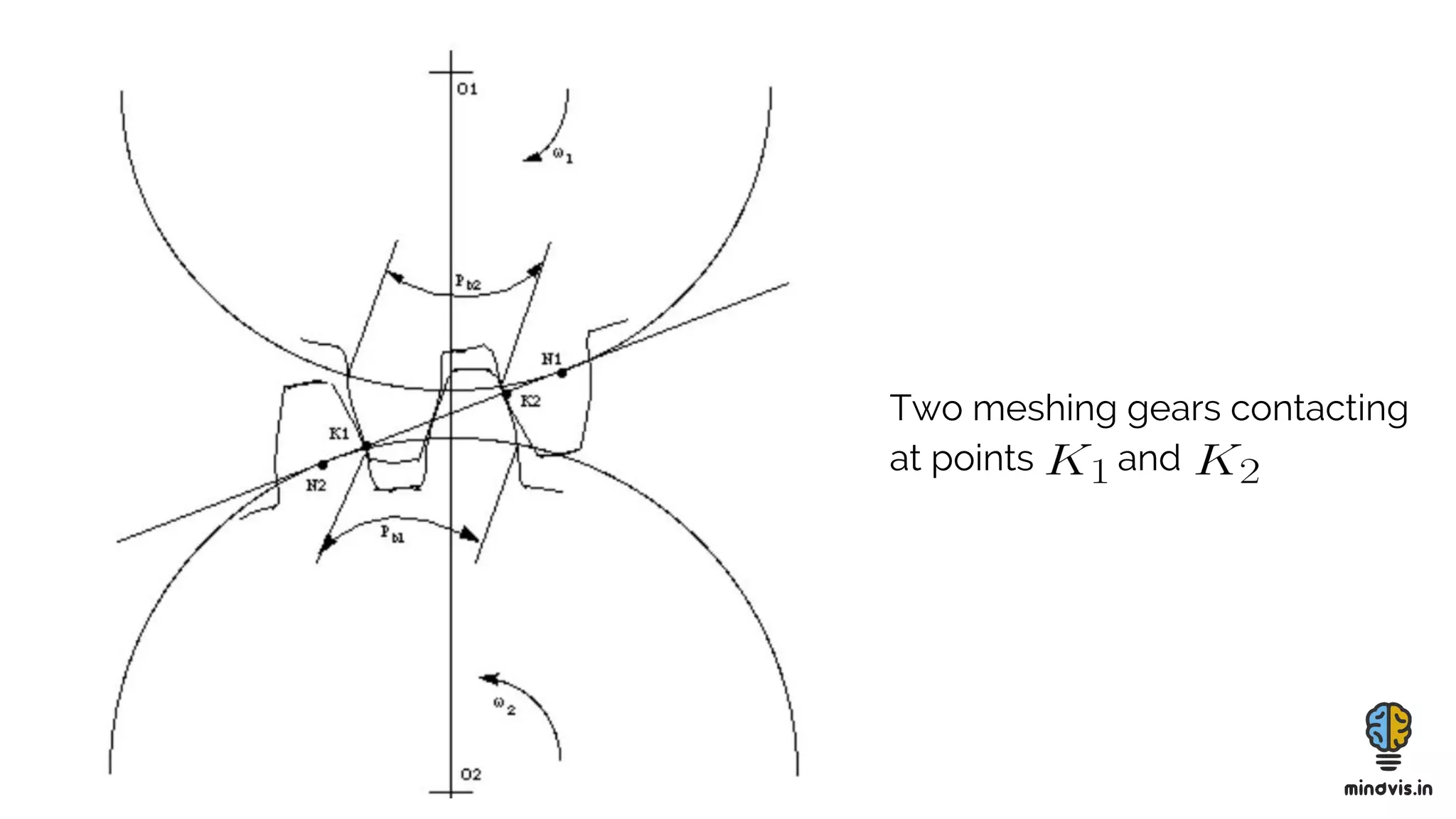
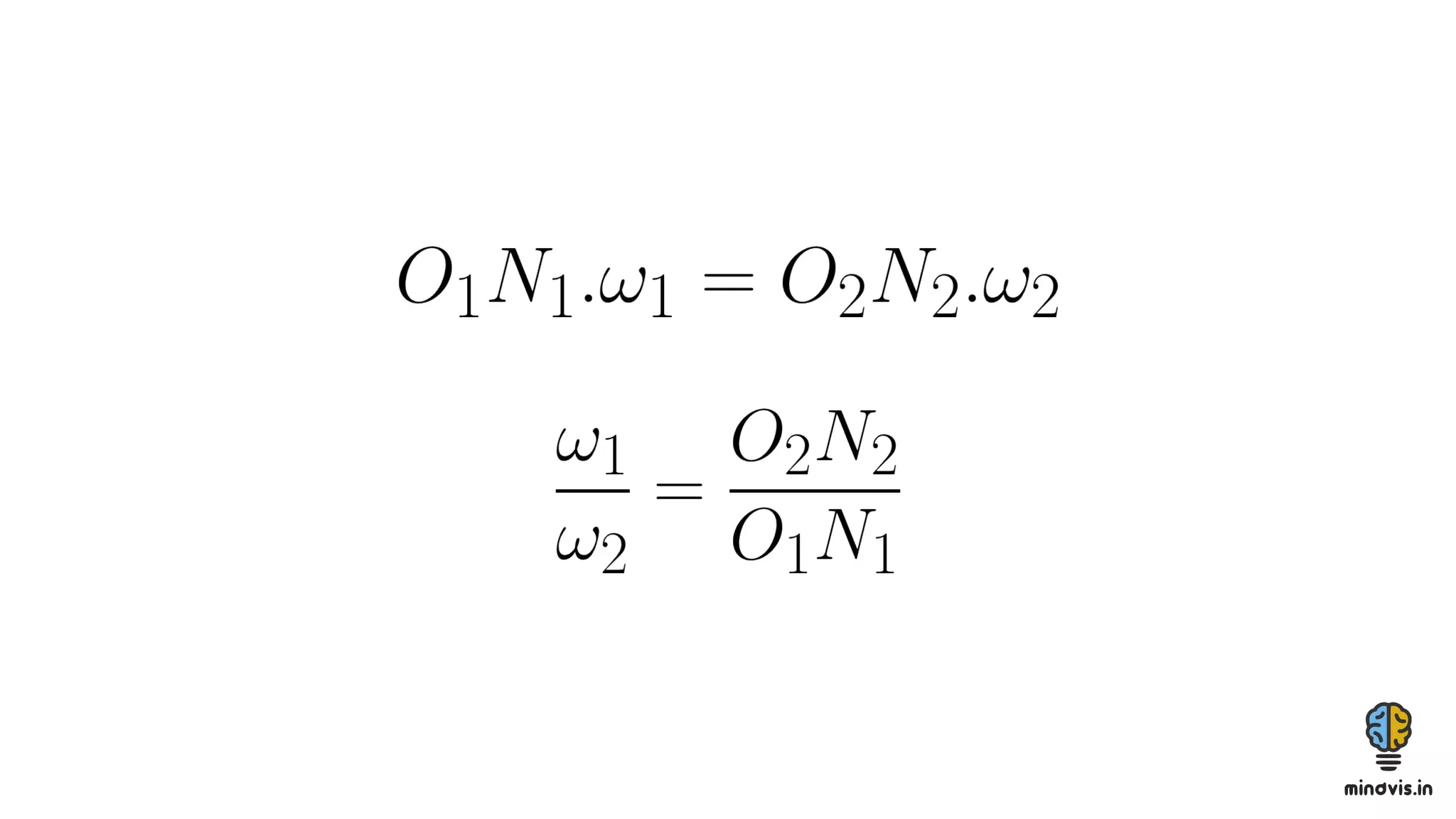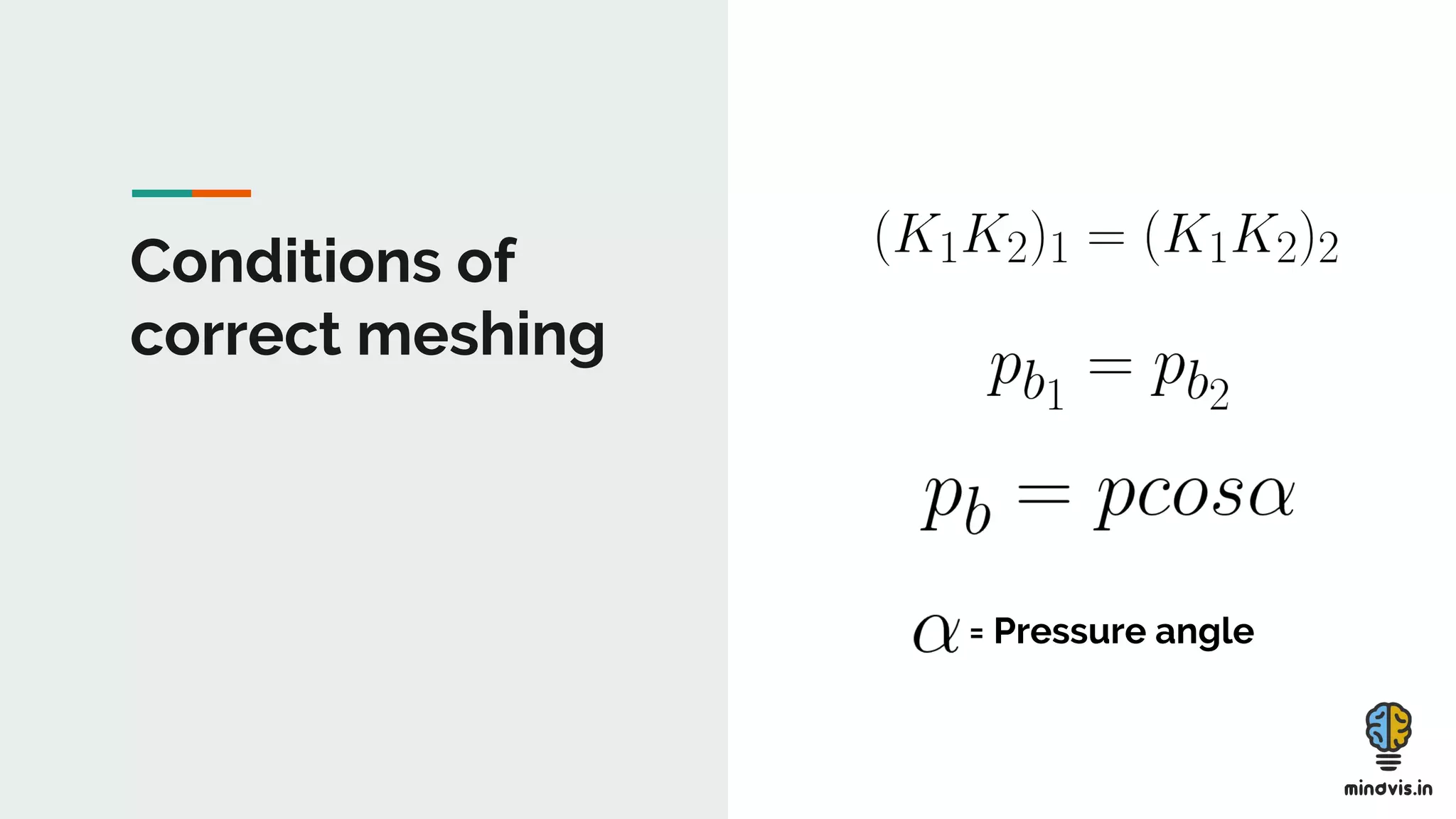The document discusses the theory of gears, including their functions, classifications, and terminology, as well as the fundamental laws of gearing and tooth profiles such as involute and cycloidal. It also covers the significance of pressure angles in gear design and troubleshooting common gear issues like pitting, scoring, and spalling. The document serves as a comprehensive guide for understanding gears and their operational principles in machinery.

1. Theory of
Machines-Gears &
Gear Trains
Er. Himanshu Vasistha

2. Why gears are used?
1) Changing the direction through which power is
transmitted (parallel, right angles, rotating, linear
etc.)
2) Changing the amount of force or torque.
3) Changing RPM.

3. Classification of gears.
Gears are classified based on the relative position of
the axes of revolution.
1. Parallel
2. Intersecting
3. Neither parallel nor intersecting

4. Gears
terminology

5. Gears nomenclature

6. Comparative Gear teeth size- Module
Using ISO (International Organization for Standardization) guidelines, Module Size is designated as the unit representing
gear tooth-sizes.
Module (m)
m = 1 (p = 3.1416)
m = 2 (p = 6.2832)
m = 4 (p = 12.566)
If you multiply Module by Pi, you can obtain Pitch (p). Pitch is the distance between corresponding points on adjacent
teeth.

7. Comparative Gear teeth size- Module
The size of gears is determined in
accordance with the reference
diameter (d) and determined by these
other factors; the base circle, Pitch,
Tooth Thickness, Tooth Depth,
Addendum and Dedendum.
Reference diameter (d)
d = zm
Tip diameter (da)
da = d + 2 m
Root diameter (df)
df ＝ d －2.5 m

9. Law of Gearing
Tooth profile 1 drives tooth profile 2 by
acting at the instantaneous contact point
K.

11. Point P is the Pitch Point. Pitch point divides the line between the line of
centers and its position decides the velocity ratio of the two teeth. The
above expression is the fundamental law of gear-tooth action.

12. Constant
velocity ratio
Condition
Position of point P
should remain
unchanged.

13. Law of gearing
Alternate definition
The common normal to the
tooth profiles at the point of
contact must always pass
through a fixed point (the
pitch point) on the line of
centers (to get a constant
velocity ratio).

14. Conjugate
profiles
To obtain the expected velocity
ratio of two tooth profiles, the
normal line of their profiles must
pass through the corresponding
pitch point, which is decided by
the velocity ratio.
The two profiles which satisfy this
requirement are called conjugate
profiles.1) Cycloidal
2) Involute

15. Involute profile
The involute curve is the path traced by a
point on a line as the line rolls without
slipping on the circumference of a circle.
It may also be defined as a path traced by
the end of a string which is originally
wrapped on a circle when the string is
unwrapped from the circle. The circle from
which the involute is derived is called the
base circle.
We use the word involute because
the contour of gear teeth curves
inward.

16. Properties of
Involute curve
1. The distance BK is equal
to the arc AB, because
link MN rolls without
slipping on the circle.
2. The normal at any point
of an involute is tangent
to the base circle.
3. There is no involute curve
within the base circle.

17. Conditions of
correct meshing

18. Two meshing gears contacting
at points and

19. Conditions of
correct meshing
= Pressure angle

20. Pressure Angle
The pressure angle exists between the
tooth profile and a radial line to its pitch
point. In involute teeth, it is defined as
the angle formed by the radial line and
the line tangent to the profile at the
pitch point.

21. Pressure Angle
At the pitch point, the gear A is pushing
the gear B. The pushing force acts
along the common normal of the gear
A and the gear B. The pressure angle
can be described as the angle between
the common normal and the line
tangent to the reference circle.

22. Significance-Pressure
Angle
1) increasing pressure angle improves the
tooth strength.
2) increasing pressure angle result in
smaller base circle so more portion of
tooth becomes involute thus can
eliminate interference.
3) increasing pressure angle will improve
power transmission but at the same time
will increase gear wear and meshing
noise
4) decreasing the pressure Angle will
require more teeth on the pinion to avoid
undercutting
5) low pressure angle will decrease
power transmission capacity but will
improve gear meshing properties like
reduced noise.

24. Gears
troubleshooting

25. Pitting
When the gear surface is repeatedly subjected to load and the
force near the contact point exceeds the material's fatigue limit,
fine cracks occur and eventually develop into separation of small
pieces, thereby creating pits (craters).
Initial Stage Pitting
The initial cause comes from small convex portions of the gear
surfaces contacting each other and the local load exceeding the
fatigue limit. As gears are driven and surfaces become worn in,
local convex portions disappear and the load is equalized and
pitting stops.
Progressive Pitting
Even after gear surfaces are worn in and load is equalized, with
time more pitting starts to occur and pits get enlarged.
(1) When an overload condition exists and the gear surface load
exceeds the fatigue limit of the material.
(2) While being driven, the load distribution could become
uneven across the gear face due to various parts' deflection
causing the fatigue limit to become exceeded.
These are some of the possible reasons of progressive pitting.

26. Scoring This is the condition in which the lubricant coating
breaks down due to overheating of local contact
areas causing the deterioration of the gear surface
from metal to metal contact. It is possible for this
condition to progress from moderate to break
down.

27. Spalling This refers to the symptom of relatively large metal
chips falling off from the gear surface due to
material fatigue below the surface from high load.
The gear surface's concave part is large and the
shape and the depth are irregular. Because the
applied shear force exceeds the material's fatigue
limit, fatigue cracks appear and grow leading to
possible breakage of the tooth.

28. Next Class Interference in Gears
Helical Gears
Gear trains

29. Email your questions
himanshu.vasistha@mindvis.in