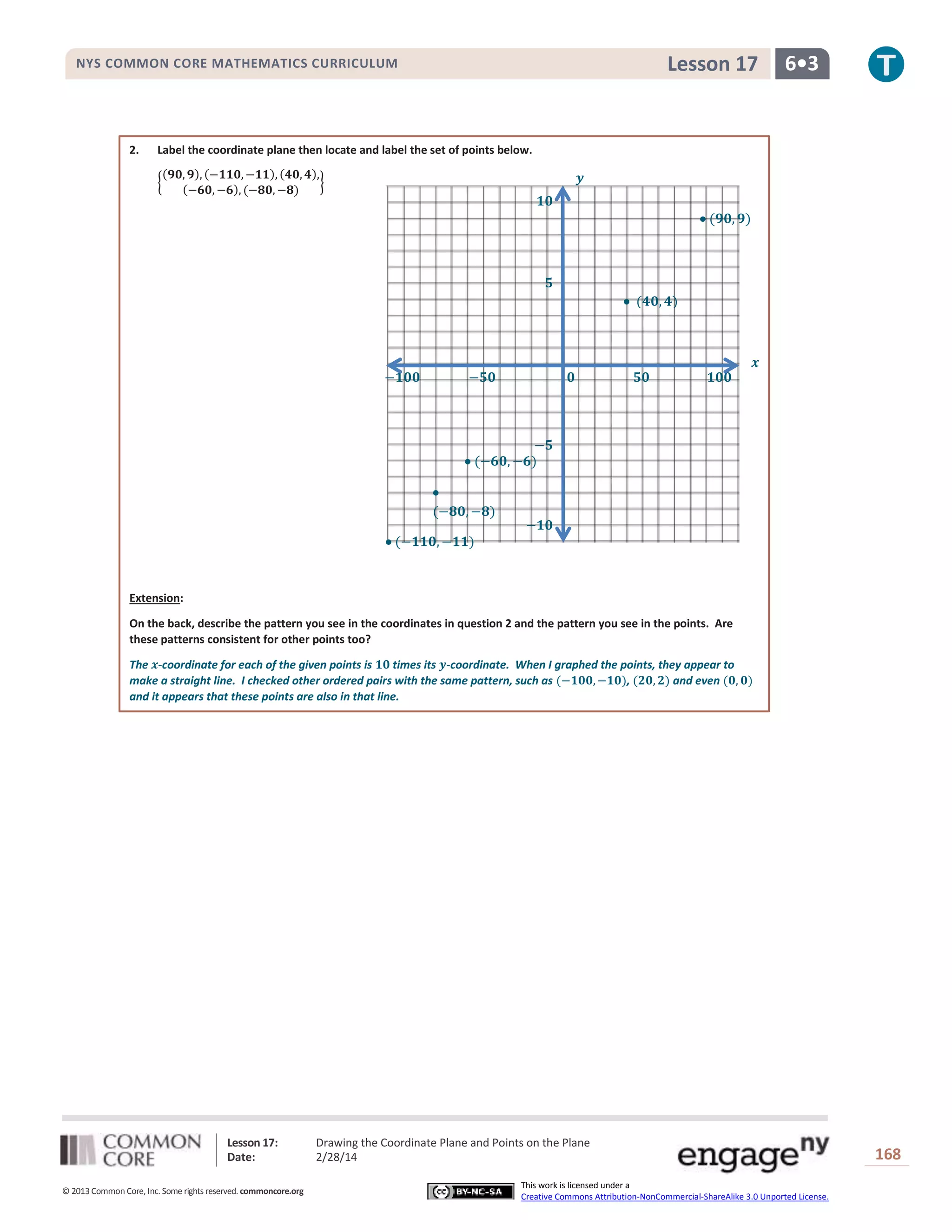
This document provides an overview of Lesson 17 from the NYS COMMON CORE MATHEMATICS CURRICULUM. The lesson teaches students how to draw coordinate planes and locate points on the plane given as ordered pairs. It includes 4 examples of drawing coordinate planes with different scales for the axes in order to properly display the given points. The lesson emphasizes the importance of first examining the range of values in a set of points before assigning scales to the axes.