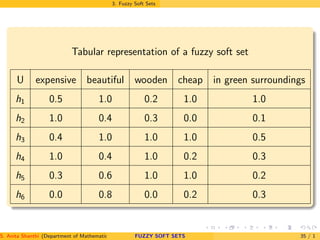
This document discusses fuzzy soft sets and soft set theory. It begins with an introduction to soft set theory as a mathematical tool for dealing with uncertainties. It then provides definitions and examples related to soft set theory, including the definition of a soft set, operations on soft sets like union and intersection, and concepts like null soft sets and absolute soft sets. The document aims to lay the foundations of soft set theory.


![2. Theory of Soft Sets
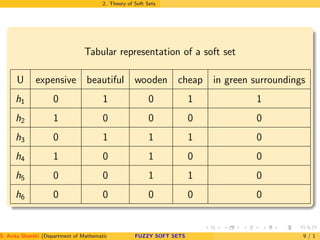
2. Theory of Soft Sets
Definition 2.1.
Let X be a non-empty set. A fuzzy set A is characterized by its
membership function µA : X → [0, 1] and µA(x) is interpreted as the
degree of membership of element x in X. A is completely determined
by the set of tuples, A = {(x, µA(x)) : x ∈ X}.
Let U be an initial universe set and E be a set of parameters. Let
P(U) denote the power set of U and A ⊂ E.
S. Anita Shanthi (Department of Mathematics, Annamalai University, Annamalainagar-608002,Tamilnadu, India. E-mail : shanthi.anita@FUZZY SOFT SETS 4 / 1](https://image.slidesharecdn.com/fuzzysoftsets-190718132346/85/Fuzzy-soft-sets-4-320.jpg)


















































![References
References
[1] K.Atannassov, Intuitionistic fuzzy sets, Fuzzy sets and systems,
20 (1986), 87-96.
[2] P.K.Maji, R.Biswas and A.R.Roy, On soft set theory, Computers
and Mathematics with Applications, 45 (2003), 555-562.
[3] P.K.Maji, R.Biswas and A.R.Roy, Fuzzy soft sets, Journal of
Fuzzy Mathematics, 9(3)(2001), 589-602.
S. Anita Shanthi (Department of Mathematics, Annamalai University, Annamalainagar-608002,Tamilnadu, India. E-mail : shanthi.anita@FUZZY SOFT SETS 57 / 1](https://image.slidesharecdn.com/fuzzysoftsets-190718132346/85/Fuzzy-soft-sets-57-320.jpg)
![References
[4] D.Molodtsov, Soft set theory-First results, Computers and
Mathematics with Applications, 37 (1999), 19-31.
[5] L.A.Zadeh, Fuzzy sets, Infor. and Control, 8 (1965), 338-353.
[6] H.J.Zimmerman, Fuzzy set theory and its applications, Kluwer
Academic Publishers, Boston, (1996).
S. Anita Shanthi (Department of Mathematics, Annamalai University, Annamalainagar-608002,Tamilnadu, India. E-mail : shanthi.anita@FUZZY SOFT SETS 58 / 1](https://image.slidesharecdn.com/fuzzysoftsets-190718132346/85/Fuzzy-soft-sets-58-320.jpg)
