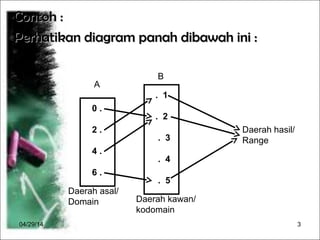
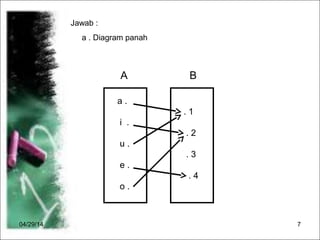
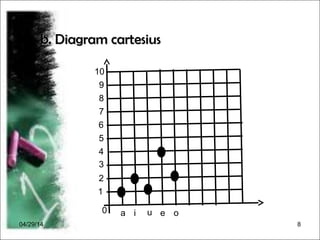
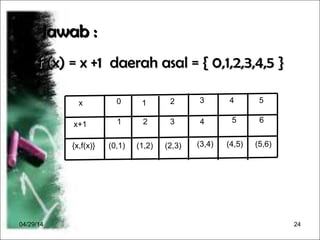
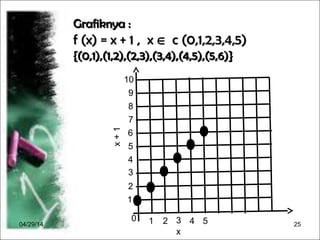
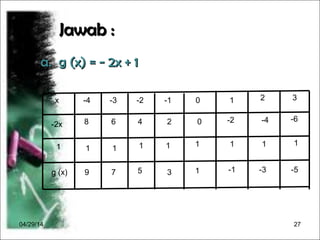
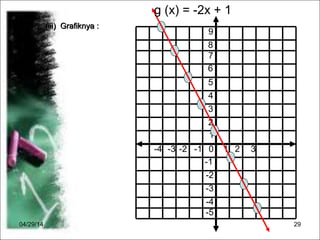
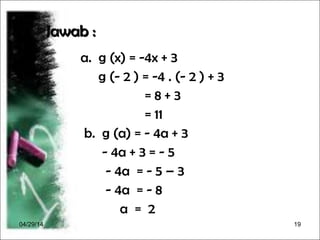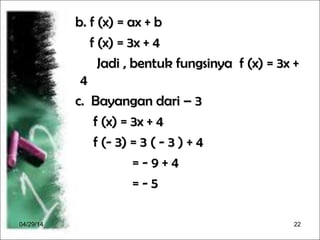Dokumen menjelaskan konsep fungsi dalam matematika, termasuk pengertian, notasi, dan cara menggambarkannya. Terdapat contoh diagram panah, cara menentukan banyaknya pemetaan antara dua himpunan, serta langkah-langkah untuk merumuskan dan menghitung nilai fungsi. Selain itu, dokumen memberikan contoh grafik fungsi dan cara menggambarnya dengan tabel.