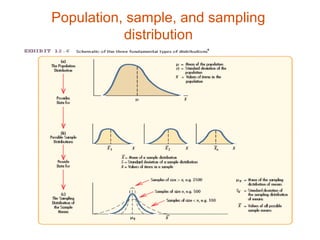
The document provides an overview of univariate statistical analysis and inferential statistics, including key concepts like population and sample distributions, measures of central tendency and dispersion, the normal distribution, sampling distributions, confidence intervals, and how these statistical techniques are used to make inferences about populations based on samples. It also discusses important steps in the data analysis process like data preparation, selecting appropriate analysis strategies and techniques based on the research objectives and data types.

1. Fundamentals of Data
Analysis
Lecture 8

2. Chapter 12
Univariate statistical analysis: A
recap of inferential statistics
2

3. Review sampling
• You want to see a new movie this weekend.
So you get onto a website and checkout
previews of what’s on.
• Is this sampling?
• How good a sample would this be>
3

4. Census vs Sampling
4

5. Learning Objectives
• Understand and explain the need for data
preparation techniques such as editing,
coding, cleaning and statistically adjusting the
data where required
• Develop a data analysis strategy based on
specific research objectives
• Identify the factors influencing the selection of
an appropriate data analysis strategy
• Outline various analysis techniques

6. Data Preparation Process
Prepare preliminary plan of data analysis

Check questionnaires

Edit

Code

Transcribe

Clean data

Statistically adjust the data

Select a data analysis strategy

7. Questionnaire Checking
• Review all questionnaires for completeness
and interviewing quality
• Unacceptable questionnaires include:
– Parts of the questionnaire that are
incomplete
– Skip patterns may not have been followed
– Little variances in responses
– Pages missing
– Late questionnaires
– Respondents does not fit the selection
criteria

8. Data Editing
• A review of the questionnaires with the
objective of increasing accuracy and
precision.
• Identify responses that are:
– Illegible
– Incomplete
– Inconsistent
– Ambiguous responses

9. Data Editing cont.
• Treatment of unsatisfactory responses
– Return to the field
• Recontact the respondent
– Assign missing values
• If the number of unsatisfactory responses is
small
• Key variables are not missing
– Discard unsatisfactory respondents (cases)
• Proportion of unsatisfactory responses is small
• Sample size is large
• Unsatisfactory respondents do not differ from
satisfactory respondents
• Responses to key variables are missing

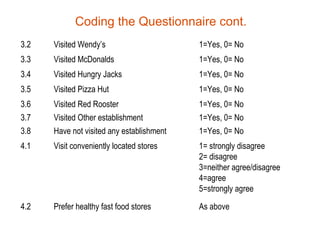
10. Data Coding
• Assigning a code [number] to each possible
response to each question [variable]
– Structured questionnaires [pre-coded]
– Unstructured questions [post-coding]
• Category codes should be mutually exclusive
and collectively exhaustive.
• Category codes should be assigned for critical
issues even if no one mentions them.

11. A Basic Questionnaire
1. In a typical month, how many times would you say you visit a fast-food restaurant? (Tick one box only)
None One Two Three Four Five Six or more
2. On your last visit to a fast-food restaurant, what was the dollar amount you spent on food and beverages?
Under $2.00 $6.01 - $10.00 More than $14.00
$2.01 - $6.00 $10.01 - $14.00 Don’t remember
3. How many of these restaurants would you say you visited in the past two months? Tick as many as apply.
KFC Pizza Hut
Wendy’s Red Rooster
McDonalds Other
Hungry jacks Have not visited any of these establishments
4. On a scale of 1 to 5, with 1 being strongly disagree to 5 being strongly agree, how would you rate fast-food
restaurants on the following dimensions:
I only visit those fast-food establishments that are conveniently located to my home 1 2 3 4 5
I prefer to visit fast-food restaurants that serve healthy/nutritious food 1 2 3 4 5
The price of food items is not important when visiting a fast-food restaurant 1 2 3 4 5
All fast-food restaurants should offer some type of child’s menu or kid’s meal 1 2 3 4 5
5. How many children do you have living at home?
None One Two Three Four Five or more
6. Which category does you total annual household income fall?
Under $20,000 $20,000 - $39,999 $40,000 - $59,999 $60,000 or more

12. Coding the Questionnaire
Variable Variable Coding
Number Name Instruction (99=missing value)
1 Number of visits per month 0=None
1=one
2= two
3=three
4=Four
5= five
6= six or more
2 Amount spent 1= Under $2
2= $2.01 - $6.00
3= $6.01 - $10.00
4= $10.01 - $14.00
5= More than $14.00
6= Don’t remember
3.1 Visited KFC 1=Yes, 0= No

13. Coding the Questionnaire cont.
3.2 Visited Wendy’s 1=Yes, 0= No
3.3 Visited McDonalds 1=Yes, 0= No
3.4 Visited Hungry Jacks 1=Yes, 0= No
3.5 Visited Pizza Hut 1=Yes, 0= No
3.6 Visited Red Rooster 1=Yes, 0= No
3.7 Visited Other establishment 1=Yes, 0= No
3.8 Have not visited any establishment 1=Yes, 0= No
4.1 Visit conveniently located stores 1= strongly disagree
2= disagree
3=neither agree/disagree
4=agree
5=strongly agree
4.2 Prefer healthy fast food stores As above

14. Coding the Questionnaire cont.
4.3 Price is important As above
4.4 Children’s menu is important As above
5 Number of children 0=None
1=one
2= two
3=three
4=Four
5= five or more
6 Annual household income 1=under $20,000
2=$20,000 - $39,000
3=$40,000 - $59,000
4=$60,000 or more

15. Transcribing
• Transferring coded data from the questionnaire to
a computer to be used for analysis.
• Variations to manual transcribing:
– CATI or CAPI
– Mark sense forms and optical scanning
– UPC
– Computerised sensory analysis systems
• For verification of the entire dataset, re-enter the
responses

16. Transcribing cont.

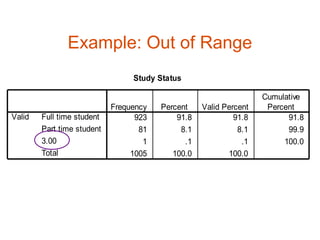
17. Data Cleaning
• Consistency check
– Out of range [see study status]
– Logically inconsistent
[e.g., does not own the product but is a heavy user]
– Extreme values
[indiscriminatingly responding the same way on all attributes]

18. Example: Out of Range
Study Status
Cumulative
Frequency Percent Valid Percent Percent
Valid Full time student 923 91.8 91.8 91.8
Part time student 81 8.1 8.1 99.9
3.00 1 .1 .1 100.0
Total 1005 100.0 100.0

19. Data Cleaning cont.
• Treatment of missing responses
– Substitute a neutral value [substitute the ‘mean’
response of the variable]
– Substitute an imputed response [use the
respondent’s pattern of responses to other
questions]
– Casewise deletion [respondents with any missing
values are discarded from the analysis]
– Pairwise deletion [use only cases or respondents
with complete responses for each calculation]

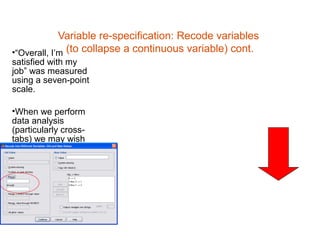
20. Statistically Adjusting the Data
• Weighting
– Each case is assigned a weight to reflect its
importance relative to other cases, often used to
make the sample more representative of a target
population
• Variable re-specification
– Transformation of data to create new variables or
modify existing variables to better suit the
research objectives by summing several variables,
log transformations, dummy variables [see next
slide]
• Scale transformation
– Manipulation of scale values to ensure
comparability with other scales or otherwise make
the data suitable for analysis [when data is not
normally distributed].

21. Variable re-specification: Composite variables
•Aesthetics of a
website
•Measured using two
items
–“The website is
visually pleasing”
–“The website is
visually appealing”
–Combine these two
items to create a new
variable “Aesthetics
of a website” – this
new variable is used
with further analysis
in place of the two
items.

22. Variable re-specification: Recode variables
(to recode negatively-worded scale items)
Role Overload Strongly Disagree Disagree Neither Agree Agree Strongly
Disagree Somewhat agree nor Somewhat Agree
disagree
I have too much work to do, to do everything 1 2 3 4 5 6 7
well
The amount of work I am asked to do is fair 1 2 3 4 5 6 7
I never seem to have enough time to get 1 2 3 4 5 6 7
everything done
•Role overload is measured by 3 items.
•Which item is reverse-coded?
•We need to code this so all item are flowing in the same
direction.
•We need to inform SPSS that 1=7, 2=6, 3= 5, 4=4, 5=3, 6=2,
7=1 for the reverse coded item.

23. Variable re-specification: Recode variables
•“Overall, I’m (to collapse a continuous variable) cont.
satisfied with my
job” was measured
using a seven-point
scale.
•When we perform
data analysis
(particularly cross-
tabs) we may wish
to have fewer
categories for
brevity.

24. Strategy for Data Analysis
• Determine the type of data which is available
[nominal, ordinal, interval, ratio]
• Decide what needs to be discussed in order to tell
‘the story’
• Choose techniques to best get information on
specific parts of what has to be discussed
• Run the results
• Determine what the results mean, what patterns
can be seen, what kind of statistical decisions
should be made
• Write about the results to explain what is going on
to someone who does not like numbers and has
never heard of statistics

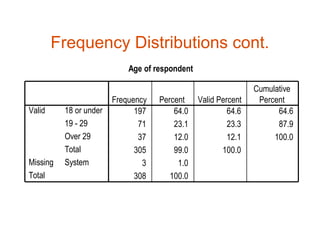
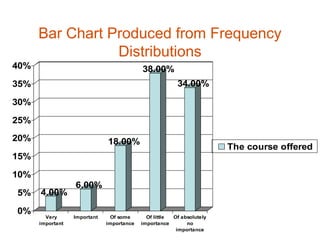
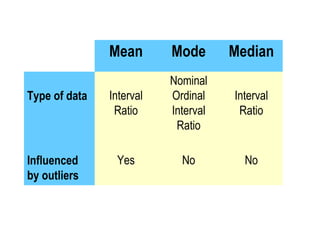
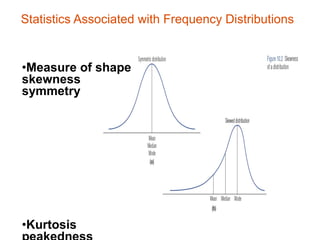
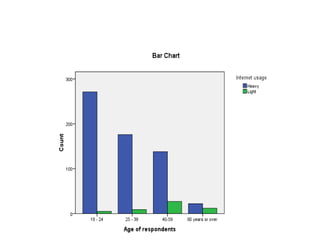
25. Overview of Techniques
• Descriptive Statistics
– Frequency distribution and cross
tabulations
– Measures of central tendency [mean,
median, mode]
– Measures of dispersion [range,
interquartile range, standard deviation]
– Shape [skewness, kurtosis]
• Inferential Statistics
– Parametric tests [Z or t test, paired t
test]
– Non-parametric tests [Chi-square]

26. Descriptive and inferential statistics
• Descriptive statistics are used to describe
characteristics of a population.
• Inferential statistics are used to make
inferences about a population from a
sample of that population.
26

27. Sample statistics and population
parameters
• Sample statistics are variables in a sample or
measures computed from sample data.
• Population parameters are variables in a
population or measured characteristics of the
population.
• But, generally we do not know what these
population parameters are and that is why we
use samples.
27

28. Frequency distributions
• Frequency distribution involves a process of
recording the number of times a particular
value of a variable occurs.
• Percentage distribution is a distribution of
relative frequency.
• Probability is the long–run relative frequency
with which an event will occur.
28

29. Frequency distributions
29

30. Measures of central tendency
• Mean: arithmetic average
• Median: the midpoint
– The value below which half the values
in a distribution fall.
• Mode: the value that occurs most often.
30

31. Measures of dispersion
• The tendency of observations to depart from
the central tendency.
• Range: distance between the smallest and
largest values.
• Deviation scores: how far any observation is
from the mean.
– Average deviation
• Variance: measure of variability or dispersion
– Its square root is the standard deviation.
31

32. Measures of dispersion
• Standard deviation: quantitative index of a
distribution’s spread.
– Using square root of variance reverts to the
original measurement units.
32

33. The normal distribution
• A symmetrical, bell–shaped distribution that
describes the expected probability distribution
of many chance occurrences.
– 99% of its values are within + 3 standard
deviations from its mean.
33

34. The normal distribution
• Standardised normal distribution has:
– symmetry about its mean
– infinite number of cases
– area under the curve with probability
density equal to 1
– mean of 0 and standard deviation of 1.
Standardised value = Value to be transformed – Mean
Standard deviation
Z=X-µ
σ
34

35. An example of standardised value
• Toy manufacturer has mean sales of 9000 units and standard
deviation of 500 units.
• Wishes to know whether wholesalers will demand between 7500
and 9635 units.
Z = X - µ = 7500 – 9000 = -3.00
σ 500
Z = X - µ = 9625 – 9000 = 1.25
σ 500
• Referring to Table 12.8, we find that:
– When Z = –3.00, the area under the curve = 0.499.
– When Z = 1.25, the area under the curve = 0.394.
– The total area under the curve = 0.499 + 0.394 = 0.893.
– There is a 0.893 probability that sales will in that range.
35

36. The standardised normal table
36

37. Population, sample, and sampling
distribution
• Population distribution: a frequency
distribution of the elements of a population.
• Sample distribution: a frequency distribution
of a sample.
• Sampling distribution: a theoretical probability
of sample means for all possible samples of a
certain size drawn from a particular
population.
37

38. Population, sample, and sampling
distribution
• Standard error of the mean: the standard
error of the sampling distribution.
• Sampling distribution is important because it
addresses the question of ‘ What would
happen if we were to draw a large number of
samples, each having n elements, from a
specified population?’
38

39. Population, sample, and sampling
distribution
39

40. Central–limit theorem
• Central–limit theorem states that as the
sample size increases, the distribution of the
mean of a random sample taken from
practically any population approaches a
normal distribution.
40

41. Confidence intervals
• A confidence interval estimate is based on
the knowledge that the population mean is
the sample mean plus or minus a small
sampling error.
– After calculating an interval estimate, we
can determine how probable it is that the
population mean will fall within this range
of statistical values.
• Confidence level is a percentage that
indicates the long–run probability that the
results will be correct.
41

42. Confidence intervals
∀ µ=X+E
where E = range of sampling error
• E = Zc.l.SX
where Zc.l. = value of Z at a specified confidence level (c.l.) and
SX = standard error of the mean
∀ µ = X + Zc.l.SX
where SX = S , S = standard deviation and n = sample size
√n
• Thus, µ = X + Zc.l.S
√n
42

43. An example of confidence intervals
• Sporting goods store caters to working women who golf.
• Survey showed the mean age is 37.5 years and standard
deviation of 12.0 years.
• Wishes to be 95% confident that the sample estimates will include
the population parameter.
µ = X + Zc.l. S = 37.5 + Zc.l. 12.0
√n √100
• Including 95% of the area requires that 47.5% of the distribution
on each side be included.
• Referring to Table B.2 in Appendix B, we find that 0.475
corresponds to the Z-value 1.96. Thus:
µ = 37.5 + (1.96)(1.2) = 37.5 + 2.352
• 95% of the time µ is in range of 35.15 to 39.85 years.
43

44. Frequency Distributions
• A count of the number of responses
associated with different values of the
variable
Where did you hear about VU's Open Day?
Cumulative
Frequency Percent Valid Percent Percent
Valid Radio 39 12.7 12.8 12.8
Newspaper 29 9.4 9.5 22.3
Internet site 25 8.1 8.2 30.5
Friend/Relation 52 16.9 17.0 47.5
School 160 51.9 52.5 100.0
Total 305 99.0 100.0
Missing System 3 1.0
Total 308 100.0

45. Frequency Distributions cont.
Age of respondent
Cumulative
Frequency Percent Valid Percent Percent
Valid 18 or under 197 64.0 64.6 64.6
19 - 29 71 23.1 23.3 87.9
Over 29 37 12.0 12.1 100.0
Total 305 99.0 100.0
Missing System 3 1.0
Total 308 100.0

46. Bar Chart Produced from Frequency
Distributions
40% 38.00%
35% 34.00%
30%
25%
20% 18.00%
The course offered
15%
10%
6.00%
5% 4.00%
0%
Very Important Of some Of little Of absolutely
important importance importance no
importance

47. Frequencies for
Multiple Response Questions
• Example of a question using multiple-response
formatting
Q9.Which of the following people had an influence on your choice of university?
Parents 01
Friends 02
Ex-VU student 03
Teacher at high school 04
Careers teacher at high school 05
Colleagues 06
Other 07

48. Frequencies for Multiple Response
Questions
Influence on choice of university
(Value tabulated = 1)
Pct of Pct of
Dichotomy label Name Count Responses Cases
Influenced by Parents Q9A 420 26.4 42.3
Influenced by friends Q9B 331 20.8 33.4
Influenced by student Q9C 149 9.4 15.0
Teacher at high school Q9D 158 9.9 15.9
Careers teacher at high school Q9E 259 16.3 26.1
Colleagues Q9F 88 5.5 8.9
Other Q9G 184 11.6 18.5
------- ----- -----
Total responses 1589 100.0 160.2

49. Statistics Associated with Frequency
Distributions: Measures of Location
• Mean
– ‘average’
• Mode
– The value that occurs most frequently.
– Most appropriate for categorical data.
• Median
– Middle value in the data set when the data are
arranged in ascending or descending order.

50. Mean Mode Median
Nominal
Type of data Interval Ordinal Interval
Ratio Interval Ratio
Ratio
Influenced Yes No No
by outliers

51. Statistics Associated with Frequency
Distributions: Measures of Variability
• Range
– The difference between the largest and smallest
values of a distribution.
• Interquartile range
– The range of a distribution encompassing the
middle 50 percent of the observations.
• Variance and Standard deviation
– Variance is the mean squared deviation of all the
values from the mean. The standard deviation
measures the average spread (deviation) from the
mean and uses values which are consistent with
the original observations.
• Coefficient of variation
– The standard deviation expressed as a
percentage of the mean.

52. Table 1: Factors students consider when selecting University

53. Statistics Associated with Frequency Distributions
•Measure of shape
skewness
symmetry
•Kurtosis

54. Cross-Tabulations
• Describes two or more variables
simultaneously

55. Expressing the data as percentages

56. Can also be presented graphically.

57. Notes on writing up results
• Do not simply repeat the numbers in the table as
part of the discussion
• The discussion should focus on the patterns in the
data
• Percentages (rather than numbers) are more
generalisable to the population,
• However, keep in mind that because of sampling
error the percentage in the population will not
exactly match that of the sample
• We rarely care about the sample itself, except
what it tells us about the population, it is supposed
to represent