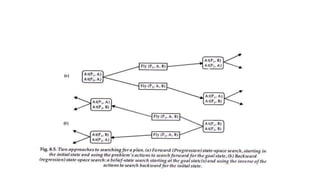
This document provides an overview of unit 4 on logical agents and planning in artificial intelligence. It discusses inference in propositional and first-order logic, logic programming, and different approaches to planning problems including state-space search, partial order planning, and both forward and backward search methods. Textbook and reference information is also provided.

1. ARTIFICIAL INTELLIGENCE
UNIT- 4
PREPARED BY
Dr. D. SUGANTHI
ASSISTANT PROFESSOR(SG)
SAVEETHA COLLEGE OF LIBERAL ARTS AND SCIENCES (SCLAS)
SIMATS, THANDALAM, CHENNAI

2. UNIT IV LOGICAL AGENTS AND PLANNING
• Inference in Propositional Logic - First-Order (Predicate) Logic -
Inference in First-Order Logic - Logic programming ; The Planning
Problem - Planning with State-Space Search - Partial Order Planning.
TEXT BOOKS
1. S. Russell & P. Norvig, “Artificial Intelligence – A Modern Approach”, Prentice-Hall, Seventh
edition, 2010
REFERENCES
1. Dan W. Patterson, “Introduction to Artificial Intelligence and Expert Systems”, Prentice-Hall,
1990.
2. K. Apt, “From Logic Programming To Prolog”, Prentice-Hall, 1996.
WEB LINKS
1. www. intellipaat.com/blog/tutorial/artificial-intelligence-tutorial
2. www. data-flair.training/blogs/ai-tutorials-home
3. www.youtube.com/watch?v=FWOZmmIUqHg
4. https://nptel.ac.in/courses/106/105/106105077/

3. Predicate Logic
A predicate is an expression of one or more variables defined on some specific domain. A predicate with variables can
be made a proposition by either assigning a value to the variable or by quantifying the variable.
The following are some examples of predicates −
•Let E(x, y) denote "x = y"
•Let X(a, b, c) denote "a + b + c = 0"
•Let M(x, y) denote "x is married to y"
Well Formed Formula
Well Formed Formula (wff) is a predicate holding any of the following −
•All propositional constants and propositional variables are wffs
•If x is a variable and Y is a wff, ∀xY∀ and ∃xY∃ are also wff
•Truth value and false values are wffs
•Each atomic formula is a wff
•All connectives connecting wffs are wffs

4. First Order Logic
• The prepositional logic only deals with the facts, that may be true or
false.
• The first order logic assumes that the world contains objects,
relations and functions.
• Syntax for first order logic:
In prepositional logic, every expression is a sentence that represents a
fact.
• First order logic includes the sentences along with terms which can
represent the objects.
• Constant symbols, variables and function symbols are used to build
terms, while quantifiers and predicate symbols are used to build the
sentences.

5. First Order logic

6. First Order logic
• Semantics:
Lets understand with an example,
Consider the sentence “Elephants are big”. There are many ways to represent this
sentence.
HasSize(Elephant, Big)
SizeOF(Elephant)= Big
Lets introduce a new syntax,
IsEqual(SizeOf(Elephant, Big), this states that a object Elephant is big, which is a useless
fact in any reasoning process about the Elephants in general. So lets represent that all
Elephants are big.
So, we can find FOL statement as,All things that are Elephants are big.
• For all things x, for which x is a Elephant, x is big.
• For all things x, if x is a Elephant, then x is big.
• Finally the FOL will be written as.
∀x Elephant (x) ⇒ Big(x)

7. Quantifiers in first-order logic
• In FOL, quantifiers allow the definition of formulae where numbers or
quantities are considered in relation to some predicates. They correspond
to indefinite adjectives in the English language, such as any, some, all or
none.
• Two types of quantifiers are provided in FOL:
• Universal quantifier. A universal quantifier means the statement is true for
everything or every instance of a particular thing within its range. g., for all,
everything, for each, for every.
• Existential quantifier. An existential quantifier expresses that the
statement is true for at least one instance of something within its scope.
E.g., for some, many, at least one
• FOL quantifiers are defined through the symbols: ∀ and ∃, which
mean all (universal) and there exists (existential), respectively. Quantifiers
always precede variables in the expressions that contain them and are
written as ∀x and ∃x. Also, if the variable refers to a predicate P(x), the
quantifier precedes the predicate and is written as ∀xP(x) and ∃xP(x).

8. KNOWLEDGE REPRESENTATION
• The term Knowledge representation, as the name suggests is the way the knowledge is
represented in the storage system of the agent. We all very well know that any of the
computer systems, the data is stored in a database.
• But there should be a proper layout of this data in the database so that the agent can
easily figure out the extracts from the present.
• In an intelligent agent, knowledge can be represented in two ways:
• Propositional logic and
• Predicate logic
• Note: At this level, we will discuss only about the first order predicate logic.
• 1) Propositional Logic
• In propositional logic, each sentence is classified as a declarative sentence. A declarative
sentence is a sentence or proposition which is either True or False. In this type of logic in
which our sentence cannot be partially correct. It has to be either completely a yes, or a
no.
• In the propositional logic, atomic sentences are combined by connectives, and each
sentence is represented by a variable. This variable is unique.

9. • A: It is hot B: It is humid Therefore, A^B represents 'It is hot
and humid'.
2) Predicate logic (First order Predicate Logic)
• In the predicate logic system of knowledge representation, it is assumed that the word contains
object, relations, and functions. The Predicate logic is a symbolized reasoning in which we can
divide the sentence into a well-defined subject and predicate.
• The subject is defined by the predicate. It should be noted that the predicate can only refer to a
single subject.
• Ravi likes peanuts
• Predicate logic for above statement: like
(Ravi,Peanuts)
• Here, Ravi is subject, like is a predicate and peanuts is
• the value that the predicate defines for the subject.

10. Knowledge Engineering of FOL
• The knowledge engineer must know about the domain to represent
the important objects and relationships.
The following steps are used to develop the knowledge base:
1. Identify the problem or task.
2. Assemble the relevant knowledge to the given problem or task.
3. Decide on a vocabulary of predicates, functions and constants.
4. Encode the general knowledge about the domain and a description
of the specific problem instance.
5. Apply queries to the inference procedure and get the answers.
6. Finally, debug the knowledge base.

11. Applications of first-order logic
• First-order logic can be useful in the creation of computer programs.
It's also of interest to researchers and practitioners in the field of
artificial intelligence (AI). There are more powerful forms of logic, but
FOL is adequate for most everyday reasoning.

12. • Propositional Logic (PL)
• Propositional logic is an analytical statement which is either true or
false. It is basically a technique that represents the knowledge in
logical & mathematical form. There are two types of propositional
logic; Atomic and Compound Propositions.

13. Facts about Propositional Logic
• Since propositional logic works on 0 and 1 thus it is also known as
‘Boolean Logic’.
• Proposition logic can be either true or false it can never be both.
• In this type of logic, symbolic variables are used in order to represent
the logic and any logic can be used for representing the variable.
• t is comprised of objects, relations, functions, and logical connectives.
• Proposition formula which is always false is called ‘Contradiction’
whereas a proposition formula which is always true is called
‘Tautology’.

14. Logic Programming
• Artificial Intelligence (AI) is the ability for an artificial machine to act
intelligently. Logic Programming is a method that computer scientists
are using to try to allow machines to reason because it is useful for
knowledge representation. In logic programming, logic is used to
represent knowledge and inference is used to manipulate it.
• The logic used to represent knowledge in logic programming is clausal
form which is a subset of first-order predicate logic. It is used because
first-order logic is well understood and able to represent all
computational problems.
• Knowledge is manipulated using the resolution inference system
which is required for proving theorems in clausal-form logic. The
diagram below shows the essence of logic programming.

15. Logic programming
• Logic programming is a programming procedure that utilizes rationale
circuits to control how rules and facts are communicated instead of
just numerical capacities. Frequently utilized in hereditary and
evolutionary programming, this methodology, by and large, mentions
to a model what objective to achieve instead of how to achieve it.
• Rather than a deliberately organized control stream directing when to
execute and how to assess work calls or different guidelines, the
program’s rationale rules are composed as logical clauses.
• Inductive logic programming is worried about summing up negative
and positive models with regards to foundation information: ML of
logic programs.

16. Logic Programming
Prolog, PROgramming in LOGic, is a declarative
programming language which is based on the
ideas of logic programming, such as those
discussed above. The idea of Prolog was to make
logic look like a programming language and allow
it to be controlled by a programmer to advance
the research for theorem-proving.

17. Logic Programming
How to improve programming logic or how to develop programming logic in
the following ways:
• Think to solve
• Practice
• Clean code
• Learn about data structures
• Play games
• Design patterns
• Look at other people’s code.
• Read books and solve examples.
• Code challenges

18. Planning in AI
We require domain description, task specification, and goal description for any planning system.
A plan is considered a sequence of actions, and each action has its preconditions that must be satisfied
before it can act and some effects that can be positive or negative.
So, we have Forward State Space Planning (FSSP) and Backward State Space Planning (BSSP) at
the basic level.

19. • 1. Forward State Space Planning (FSSP)
• FSSP behaves in the same way as forwarding state-space search. It says that given an
initial state S in any domain, we perform some necessary actions and obtain a new state
S' (which also contains some new terms), called a progression. It continues until we reach
the target position. Action should be taken in this matter.
• Disadvantage: Large branching factor
• Advantage: The algorithm is Sound
• 2. Backward State Space Planning (BSSP)
• BSSP behaves similarly to backward state-space search. In this, we move from the target
state g to the sub-goal g, tracing the previous action to achieve that goal. This process is
called regression (going back to the previous goal or sub-goal). These sub-goals should
also be checked for consistency. The action should be relevant in this case.
• Disadvantages: not sound algorithm (sometimes inconsistency can be found)
• Advantage: Small branching factor (much smaller than FSSP)

20. Planning with State-Space Search
• In artificial intelligence and computer programming, state space
planning is a process used in designing programs to search for data or
solutions to problems.
• In a computer algorithm that searches a data structure for a piece of
data, the state space is a collective term for all the data to be
searched.
• Similarly, artificial intelligence programs often employ a process of
searching through a finite universe of possible procedures for
reaching a goal, to find a procedure or the best procedure to achieve
the goal.
• The universe of possible solutions to be searched is called the state
space. State space planning is the process of deciding which parts of
the state space the program will search, and in what order.

22. • i. Forward State-Space Search:
• Planning with forward state-space search is similar to the problem-
solving approach. It is sometimes called progression planning,
because it moves in the forward direction.
• We start with the problem’s initial state, considering sequences of
actions until we reach a goal state.
• The formulation of planning problem as state-space search
problems is as follows:

23. Forward State-Space Search
• i. The initial state of the search is the initial state from the planning
problem. In general each state will be set of positive ground literals;
literals not appearing are false.
• ii. The actions which are applicable to a state are all those whose
preconditions are satisfied. The successor state resulting from an
action is generated by adding the positive effect literals and deleting
the negative effect literals.
• iii. The goal test checks whether the state satisfies the goal of the
planning problem.
• iv. The step cost of each action is typically 1. Although it would be
easy to allow different costs for different actions, this was seldom
done by STRIPS planners.

24. ii. Backward State-Space Search:
• Backward search can be difficult to implement when the goal states are
described by a set of constraints which are not listed explicitly. In particular,
it is not always obvious how to generate a description of the possible
predecessors of the set of goal states. The STRIPS representation makes
this quite easy because sets of states can be described by the literals which
must be true in those states.
• The main advantage of backward search is that it allows us to consider only
relevant actions. An action is relevant to a conjunctive goal if it achieves
one of the conjuncts of the goal. For example, the goal in our 10-airport air
cargo problem is to have 20 pieces of cargo at airport B, or more precisely.
• At (C1 B) ∧ At (C2 B)……………….. At (C20, B) then
• Thus, the predecessor description is:
• In(C1, p) ˄ At(p, B) ˄ At(C2, B) ˄……………………˄ At (C20,B)

25. Partial Order Planning
• The idea of a partial-order planner is to have a partial ordering
between actions and only commit to an ordering between actions
when forced. This is sometimes also called a non-linear
planner, which is a misnomer because such planners often produce a
linear plan.
• A partial ordering is a less-than relation that is transitive and
asymmetric. A partial-order plan is a set of actions together with a
partial ordering, representing a "before" relation on actions, such that
any total ordering of the actions, consistent with the partial ordering,
will solve the goal from the initial state. Write act0 < act1 if
action act0 is before action act1 in the partial order. This means that
action act0 must occur before action act1.