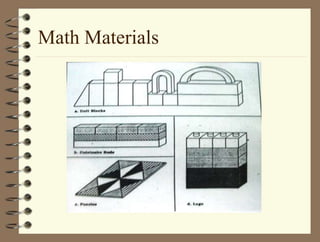
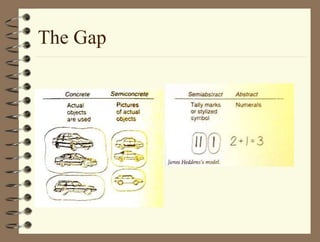
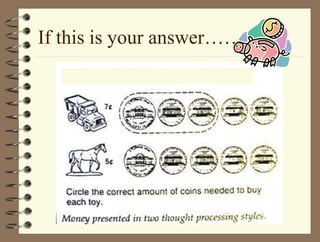
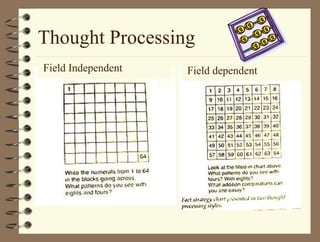
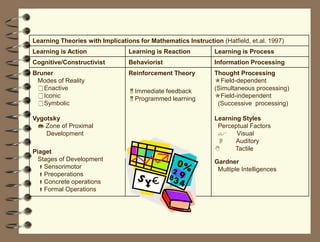
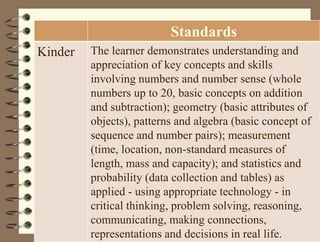
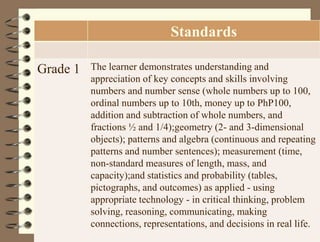
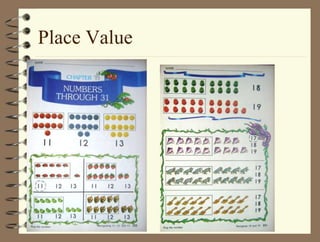
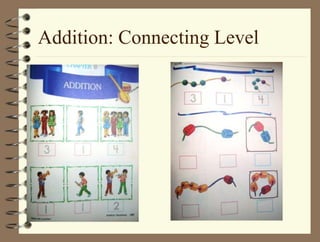
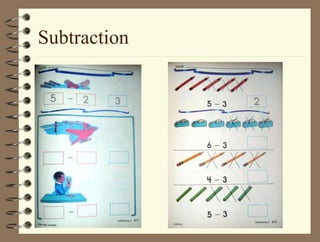
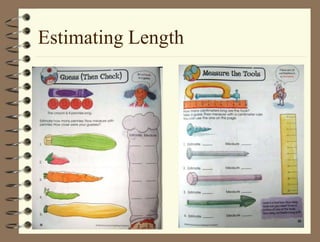
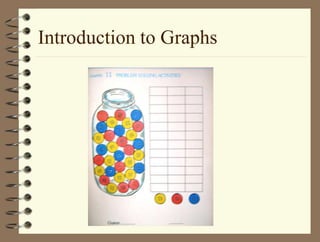
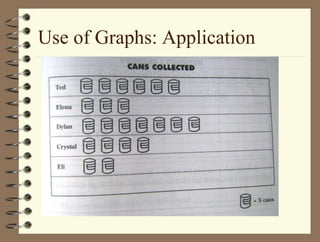
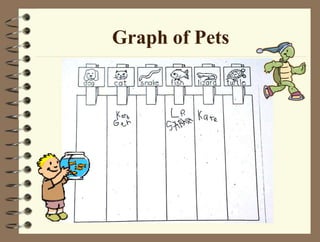
The document outlines a teaching session focused on K-3 mathematics education, covering how children learn mathematics, necessary content and competencies, and effective teaching and assessment strategies. It discusses various learning theories, including cognitive and constructivist approaches, and standards for K-3 learners in areas such as numbers, geometry, and measurement. Emphasis is placed on active learning, understanding processes, and utilizing different instructional strategies to foster critical thinking and problem-solving skills.

1. On Teaching and Learning
Mathematics :
Developing & Assessing Math
Skills
Prof. Leonor Ercillo Diaz, PhD.
UP College of Education

2. Outline of the Session
How do the K-3 children learn Mathematics?
What do they have to learn in Mathematics?
(a look into standards, content &
competencies)
How do we teach and assess Mathematics
skills?

3. How do Kids Really Learn Math
Is Math a set of
answers to
questions?
Is Math a process of
investigation and
exploration? Are kids
allowed to actively work
with materials & ideas?
Is short-term
success the goal?
Do we aim for long term
understanding?

4. How do Kids Really Learn Math
Is there much rote
learning involved?
Are we allowing kids
to think and figure
things out?
Is the goal for future
application?
Is our purpose
immediate
application?
Are the steps in
solving specified by
the teacher?
Are the students also
allowed to discover the
steps?

5. Learning Theories with Implications
for Math Instruction (Hatfield, et.al. 1997)
Learning is Action
Learning is Reaction
Learning is Process

6. Learning Theories with Implications for
Math Instruction (Hatfield, et.al. 1997)
Learning is Action
Cognitive/Constructivist
Bruner - Modes of Reality
Enactive - action on reality on concrete
ways w/o the need for imagery, inference,
or words

7. Math Materials

8. Learning Theories with Implications for
Math Instruction (Hatfield, et.al. 1997)
Learning is Action
Cognitive/Constructivist
Bruner - Modes of Reality
Enactive
Iconic – pictorial need to represent reality;
internal imagery that stands for a concept
Symbolic –abstract, arbitrary systems of
thought

9. The Gap

10. Learning Theories with Implications for
Math Instruction (Hatfield, et.al. 1997)
Learning is Action
Cognitive/Constructivist
Vygotsky
 Zone of Proximal Development
The area where the child cannot solve a
problem alone but can be successful
under adult guidance or in collaboration
with a more abled peer.

11. Zone of Proximal Development
Upper Limit
Instruction through
guidance or assistance
Lower Limit

12. Break Time: Storytime
•What are some things
that you want more of?
•Find out why the
character says “More for
Me”. What does he want
more of?
•At the end of the story,
guess the age of the
character.

27. Think Back
•Why does the character say
“More for Me”. What does he
want more of?
•Guess the age of the character.
What grade is he in?
•Why do you say so? What are
his characteristics?

28. Learning Theories with Implications for
Math Instruction (Hatfield, et.al. 1997)
Learning is Action
Cognitive/Constructivist (Piaget)
Stages of Development
Sensorimotor – actions on objects
Preoperations – actions on reality
Concrete operations -
Formal Operations

29. Pre-operations Stage
Egocentrism
Centration
Irreversible Thought
Static Thought

30. Preoperation Concrete Operational
Egocentrism
Centration
Irreversible thought
Intuitive thought
Lack of :
 conservation
 class inclusion
 transitive interference
Can see others have
diff. viewpoints
Decentration
Reversible Thought
Dynamic Thought
Conservation
Class inclusion
Transitive
Interference

31. Learning Theories with Implications for
Math Instruction (Hatfield, et.al. 1997)
Learning is Reaction
Behaviorist
Reinforcement Theory
Immediate feedback
Programmed learning

32. Immediate Feedback Activities

33. Immediate Feedback Activities

34. Immediate Feedback Activities

35. Information Processing
How we encode, store and retrieve
information
Thought Processing
Learning Styles

36. Rewind Time!

•Which of the
next two
activities do
your pupils
answer easier?

37. Activity One

38. Activity Two

39. Information Processing
Thought Processing
Strategies used to organize and classify
new information or skills to obtain
order out of a confusing series of
stimulus events.

40. If this is your answer……

41. Learning Theories with Implications for
Math Instruction (Hatfield, et.al. 1997)
Learning is Process
Information Processing
Thought Processing
Field-dependent (Simultaneous
processing)
requires stimulus materials to be
presented all at once, seeing the whole
before its parts; look for patterns to
break down the whole into its respective
parts to arrive at a solution

42. If this is your answer…..

43. Learning Theories with Implications for
Math Instruction (Hatfield, et.al. 1997)
Learning is Process
Information Processing
Thought Processing
 Field-independent (Successive processing)
requires stimulus to be presented from 1
component to the next, leading from detail to
detail until the whole is seen; build parts into
the whole to arrive at solution

44. Thought Processing
Field dependent •Field independent

45. Thought Processing
Field dependent
Field Independent

46. Learning Theories with Implications for
Math Instruction (Hatfield, et.al. 1997)
Learning is Process
Information Processing
Learning Styles
 Perceptual Factors – Preference for
materials presented through one or
more of the 5 senses
 Visual
 Auditory
F Tactile

47. Learning Styles: An Overview
Perceptual Time Mobility
Stimuli Elements
Physical

48. Learning Theories with Implications
for Math Instruction (Hatfield, et.al. 1997)
Learning is Process
Gardner’s Multiple Intelligences
Nine intelligences

49. Nine Intelligences (Gardner)
The Multiple Intelligences Pizza:
Nine Intelligences
MUSIC NATURE
SMART SMART
Musical Naturalistic
Intelligence Intelligence
Interpersonal PEOPLE BODY Bodily-
Intelligence SMART SMART Kinesthetic
Intelligence
Linguistic Logical-
Intelligence Mathematical
Intelligence
WORD LOGIC
SMART SMART
SELF PICTURE
SMART SMART
Intrapersonal
Intelligence Spatial
Intelligence

50. Learning Theories with Implications for Mathematics Instruction (Hatfield, et.al. 1997)
Learning is Action Learning is Reaction Learning is Process
Cognitive/Constructivist Behaviorist Information Processing
Bruner
Modes of Reality
Enactive
Iconic
Symbolic
Vygotsky
 Zone of Proximal
Development
Piaget
Stages of Development
Sensorimotor
Preoperations
Concrete operations
Formal Operations
Reinforcement Theory
Immediate feedback
Programmed learning
Thought Processing
Field-dependent
(Simultaneous processing)
Field-independent
(Successive processing)
Learning Styles
Perceptual Factors
 Visual
 Auditory
 Tactile
Gardner
Multiple Intelligences

51. Good job! 

52. Standards
Kinder The learner demonstrates understanding and
appreciation of key concepts and skills
involving numbers and number sense (whole
numbers up to 20, basic concepts on addition
and subtraction); geometry (basic attributes of
objects), patterns and algebra (basic concept of
sequence and number pairs); measurement
(time, location, non-standard measures of
length, mass and capacity); and statistics and
probability (data collection and tables) as
applied - using appropriate technology - in
critical thinking, problem solving, reasoning,
communicating, making connections,
representations and decisions in real life.

53. Standards
Grade 1 The learner demonstrates understanding and
appreciation of key concepts and skills involving
numbers and number sense (whole numbers up to 100,
ordinal numbers up to 10th, money up to PhP100,
addition and subtraction of whole numbers, and
fractions ½ and 1/4);geometry (2- and 3-dimensional
objects); patterns and algebra (continuous and repeating
patterns and number sentences); measurement (time,
non-standard measures of length, mass, and
capacity);and statistics and probability (tables,
pictographs, and outcomes) as applied - using
appropriate technology - in critical thinking, problem
solving, reasoning, communicating, making
connections, representations, and decisions in real life.

54. Standards
Grade 2 The learner demonstrates understanding and appreciation
of key concepts and skills involving numbers and number
sense (whole numbers up to 1 000, ordinal numbers up to
20th, money up to PhP100, the four fundamental
operations of whole numbers, and unit fractions); geometry
(basic shapes, symmetry, and tessellations); patterns and
algebra (continuous and repeating patterns and number
sentences);measurement (time, length, mass, and capacity);
and statistics and probability (tables, pictographs, and
outcomes) as applied - using appropriate technology - in
critical thinking, problem solving, reasoning,
communicating, making connections, representations, and
decisions in real life.

55. Standards
Grade 3 The learner demonstrates understanding and appreciation of
key concepts and skills involving numbers and number sense
(whole numbers up to 10 000; ordinal numbers up to 100th;
money up to PhP1 000;the four fundamental operations of
whole numbers; proper and improper fractions; and similar,
dissimilar, and equivalent fractions); geometry (lines,
symmetry, and tessellations); patterns and algebra (continuous
and repeating patterns and number sentences); measurement
(conversion of time, length, mass and capacity, area of square
and rectangle); and statistics and probability (tables, bar
graphs, and outcomes) as applied - using appropriate
technology - in critical thinking, problem solving, reasoning,
communicating, making connections, representations, and
decisions in real life.

56. Content: K-3
Numbers & Number Sense
Measurement
Geometry
Patterns & Algebra
Statistics & Probability

57. Building the Concept of Number
Counting
–Rote Counting
–Rational Counting
–Writing Numerals

58. Numbers and Counting
Rote counting
saying from memory the names of the
numerals in order.
Rational counting
attaching the number names in order to
items in a group to find out the total
number of items in the group.

59. Counting

60. Place Value

61. Estimation

62. Operations of Whole Numbers

63. Addition: Connecting Level

64. Addition: Symbolic Level

65. Addition: Other Forms

66. Addition Sentences

67. Addition Exercises

68. Subtraction

69. Subtraction

70. Subtraction: Other Forms

71. Addition & Subtraction:
Number Sentences

72. Number Sense of Fractions

73. Geometry

74. Shapes
What objects do we use to
teach shapes?

76. Shapes

77. Shapes

78. Shapes

79. Shapes

80. Shapes : Enrichment

81. More Shapes

82. Introducing a Lesson on
Geometry

83. Patterns & Algebra

84. Patterns
 Patterning includes auditory,
visual, and physical motor
sequences that are repeated.
 Patterns may be :
formed, verbally described,
copied, created and extended

85. What should come next?

86. Patterns
 Patterns have to be repeated
at least twice….

87. Patterns

88. Patterns

89. Other Patterns
3, 5, 7, 9, ____
1Z, 2Y, 3X, ___, ___, 6U
10, ___, ___, ___, ___, 60, 70
1000, 2000, 4000, ____, 16 000
100, 110, 130, ___, 250

90. Measurement

91. Measurement
Days, Months
Understanding the calendar
Time
Length
Mass:
Capacity
Area

92. Measuring Length:
Non Standard Units

93. Estimating Length

94. Use of standard units
Comparison using standard
units
Conversions
Problem Solving

95. Statistics & Probability
 Graphs
 Children can put into a picture
form the results of classifying,
comparing, counting and
measuring activities.

96. Introduction to Graphs

97. Introduction to Graphs

98. Introduction to Graphs

99. Use of Graphs: Application

100. Statistics

101. Graph of Pets

102. Birthday Chart