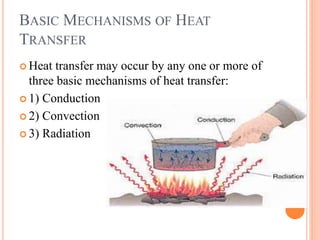
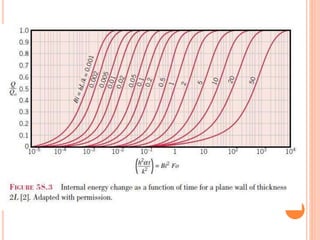
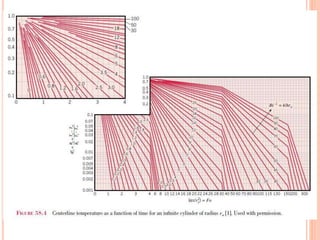
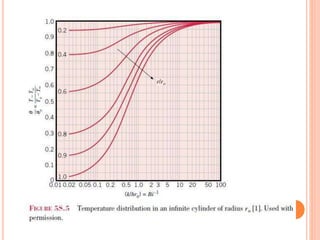
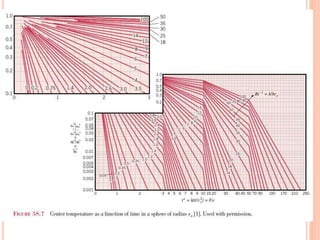
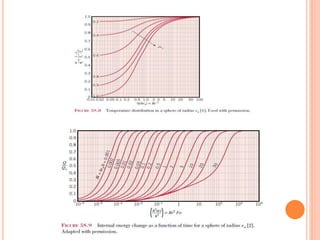
This document summarizes a presentation on heat transfer mechanisms including conduction, convection, and radiation. It discusses key concepts like temperature, heat, the three mechanisms of heat transfer, conduction, Biot number, Fourier number, and Heisler charts. Conduction involves transfer of kinetic energy between adjacent molecules. Biot and Fourier numbers are dimensionless parameters used in heat transfer calculations to characterize conduction regimes and transient behavior. Heisler charts provide a graphical tool to analyze heat transfer problems.

1. LIBRARY PAPER PRESENTATION
OF
FOOD ENGINEERING 2
CONDUCTION,CONVECTION & RADIATION
PRESENTED BY
GAURAV PATEL

2. CONTENT
 Brief about Temperature and Heat
 Basic Mechanisms of Heat Transfer
 Conduction
 Biot number and application
 Fourier number and application
 Heisler chart

3. TEMPERATURE
 It is a measure of warmth or coldness of an object
with respect to some standard value.
 The temperature of two systems is same when the
systems are in thermal equilibrium.
 Temperature conversion formula:
C/5=F-32/9=K-273/5=R/4

4. HEAT
 It is a form of energy associated with the movement of
atoms and molecules in any material.
 Heat always itself flow from higher temperature to the
lower temperature.

5. BASIC MECHANISMS OF HEAT
TRANSFER
 Heat transfer may occur by any one or more of
three basic mechanisms of heat transfer:
 1) Conduction
 2) Convection
 3) Radiation

6. CONDUCTION
 Heat can be conducted through solids, liquids, and
gases.
 Heat is conducted by the transfer of energy of motion
b/w two adjacent molecules.
 Energy can also be transferred by ‘free’ electrons
which is important in metallic solids.
 Ex: Heat treatment of steel forgings.
 It follow Fourier law of conduction:
dq/dA= k(-dt)/dx

7. STEADY STATE VS. UNSTEADY STATE HEAT
CONDUCTION
 1) Temp. constant
with time.
 2) No variation of
rate of heat transfer.
 3) The change of
internal energy in a
given time interval
will be zero.
 1) Temp. varies with
time.
 2) Variation of rate of
heat transfer .
 3) The change of
internal energy in a
given interval will not
be zero.
Steady state Unsteady state

8. BIOT NUMBER
 The Biot number (Bi) is a dimensionless quantity used
in heat transfer calculations.
 It is the ratio of resistance to internal heat flow to the
resistance to external heat flow.
Where:
h= Convective HT Coefficient
Kb=Thermal conductivity of the body
Lc= characteristic length which is defined as the volume
of the body divided by the surface area of the body.

9. APPLICATION
 If values of the Biot number is smaller than 0.1
then it indicate that the heat conduction inside
the body is much faster than the heat convection
away from its surface, and temperature
gradients are negligible inside of it.
 Then transient problem can be treated by the
“lumped thermal capacity” approach.
 The lumped capacity assumption implies that the
object for analysis is considered to have a single
mass averaged temperature.

10. CONTD.
 A Biot number greater than 0.1 (a "thermally
thick" substance) indicates that one cannot make
this assumption, and more complicated heat
transfer equations for "transient heat conduction"
will be required to describe the time-varying and
non-spatially-uniform temperature field within
the material body.
 Analytic methods for handling these problems,
which may exist for simple geometric shapes
and uniform material thermal conductivity are
described in the article on the heat equation.

11. FOURIER NUMBER
 It is a dimensionless number that characterizes
transient heat conduction.
 It is the ratio of conductive or diffusive transport
rate to the quantity storage rate where the
quantity may be either heat or matter.
Fourier No.(Fo)=
conductive transport rate/storage rate

12. CONTD.
 Thermal Fourier number (Foh )is defined by the
conduction rate to the rate of thermal energy
storage
 where:
 α= thermal diffusivity
 t= characteristic time
 L = length through which conduction occurs
 α = λ/pc ,
λ = thermal conductivity, ρ= the density
and c = specific heat)
Foh = αt/L^2

13. APPLICATION
 For unsteady state conduction problems in
solids, the Fourier number is frequently used as a
non dimensional time parameter.
 Together with the Biot number the Fourier
number can be used to determine the heating or
cooling of an object.

14. HEISLER CHART
 Heisler charts are a graphical analysis tool for the
evaluation of heat transfer in thermal engineering.
 They are a set of two charts per included geometry
introduced in 1947 by M. P. Heisler which were
supplemented by a third chart per geometry in 1961
by H. Grober.
 Heisler charts permit evaluation of the central
temperature for transient heat conduction through an
infinitely long plane wall of thickness 2L, an infinitely
long cylinder of radius ro, and a sphere of radius ro.

20. LIMITATIONS
 1) Body must be at uniform temperature initially.
 2) The temperature of the surroundings and the
convective heat transfer coefficient must remain
constant and uniform.
 3) There must be no heat generation from the
body itself.

21. REFERENCE
 Transport processes and Separation processes
principles by Christie John Geankoplis.
 Fundamentals of food engineering by D.G.RAO.
 www.nptel.ac.in.
 www.me.umn.edu.
 Wikipedia.org