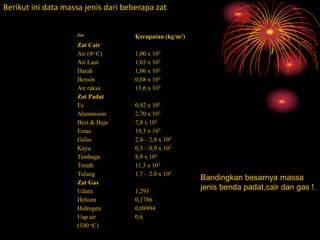
Dokumen ini membahas tentang konsep massa jenis, tekanan, dan sifat-sifat fluida, menjelaskan cara mengukur massa jenis zat serta hukum-hukum fisika terkait fluida seperti hukum Pascal dan Archimedes. Contoh perhitungan massa jenis dan tekanan diberikan untuk menyoroti aplikasinya dalam konteks nyata. Selain itu, dijelaskan pula tentang fenomena kapilaritas dan tegangan permukaan dalam zat cair.

2. Massa jenis zat (ρ)
Cara mengukur massa jenis zat
Misalnya massa jenis air :
1. Timbang massa air dengan
neraca
2. Ukur volume air dengan gelas
ukur
3. Bagi massa air dengan
volume air yang telah di
ukur

3. Jadi massa jenis zat adalah
perbandingan antara massa
dengan volume zat
Secara matematis di rumuskan:
ρ = m / V
Dengan :
m = massa
V = volume zat
ρ = kerapatan = massajenis

4.  Apabila kerapatan suatu benda lebih
kecil dari kerapatan air, maka benda
akan terapung.
Sebaliknya jika kerapatan suatu benda
lebih besar dari kerapatan air, benda
tersebut akan tenggelam.
Berat jenis suatu zat merupakan
perbandingan berat zat tersebut terhadap
volumenya. Satuan sistem internasional
untuk berat jenis adalah N/m3.

5. Zat Kerapatan (kg/m3)
Zat Cair
Air (4o C) 1,00 x 103
Air Laut 1,03 x 103
Darah 1,06 x 103
Bensin 0,68 x 103
Air raksa 13,6 x 103
Zat Padat
Es 0,92 x 103
Aluminium 2,70 x 103
Besi & Baja 7,8 x 103
Emas 19,3 x 103
Gelas 2,4 – 2,8 x 103
Kayu 0,3 – 0,9 x 103
Tembaga 8,9 x 103
Timah 11,3 x 103
Tulang 1,7 – 2.0 x 103
Zat Gas
Udara 1,293
Helium 0,1786
Hidrogen 0,08994
Uap air
(100 oC)
0,6
Berikut ini data massa jenis dari beberapa zat.
Bandingkan besarnya massa
jenis benda padat,cair dan gas !.

6. Contoh
Sepotong emas yang bentuknya seperti sepeda akan di tentukan
massanya. Emas di masukkan dalam gelas ukur yang sebelumnya
telah berisi air, seperti gambar . Ternyata , skala yang ditunjukan
oleh pemukaan air dalam gelas ukur bertambah 3,75 cm 3 . Bila
massa jenis emas = 19,3 gram/cm3 , berapakah massa emas
tersebut .
Diket :
ρ = 19,3 gr/cm 3
V = 3, 75 cm 3
Ditanya : m
Jawab :
m = ρV
= 19,3 x 3,75
= 27,375 gram

7. Tekanan ( p )
Tekanan adalah gaya yang bekerja tegak lurus pada suatu
bidang tiap satuan luas bidang yang dikenai gaya
Di rumuskan :
P = F / A
dengan :
F = gaya yang bekerja pada benda (Newton)
A = luas penampang benda(m2)
1 pascal ( 1 Pa) = 1 N/m2
Satuan lain yang digunakan = atm (atmosfer), cm
Hg, mb(milibar)
1 bar = 105 Pa 1 atm = 76 cm Hg=1,01 .105 Pa
1 mb = 10-3 bar

8. Fluida ( zat alir) : zat yang bisa mengalir.
Contohnya zat cair dan gas. Zat cair
termasuk fluida yang inkompressibel, artinya
pada tekanan yang tidak terlalu besar,
volumenya tidak berubah meskipun ditekan.
Gas termasuk fluida kompressibel, artinya
volumenya bisa berkurang jika ditekan
Air dalam keadaan diam disebut hidrostatis

9. Sifat-sifat fluida:
1. Gaya-gaya yang dikerjakan suatu fluida pada
dinding wadahnya selalu berarah tegak lurus
terhadap dinding wadahnya.
2. Tekanan dalam suatu fluida pada kedalaman yang
sama adalah sama dalam segala arah

10. Tekanan Hidrostatis (Ph)
Di rumuskan
Ph = F / A
= mg / A
= Vg / A
=  A h g / A
=  g h
= massa jenis zat cair
h= kedalaman g= percepatan gravitasi
Tekanan yang disebabkan oleh fluida tak bergerak disebut
tekanan hidrostatik

11. Tekanan Gauge
Yaitu selisih antara tekanan
yang tidak diketahui dengan
tekanan atmosfer (tekanan
udara luar)
Nilai tekanan yang diukur oleh alat pengukur tekanan
menyatakan tekanan gauge, sedangkan tekanan
sesungguhnya disebut tekanan mutlak
Pmutlak = P gauge + P atmosfer

12. Contoh :
Sebuah ban berisi
udara bertekanan
gauge 2 bar memiliki
tekanan mutlak kira-
kira 3 bar, sebab
tekanan atmosfer
pada permukaan laut
kira-kira 1 bar

13. Contoh Soal : 2
Sebuah logam paduan ( alloy ) dibuat dari 0,04
kg logam A dengan massa jenis 8000 kg/m3
dan 0,10 kg logam B dengan massa jenis 10000
kg/m3 . Hitung massa jenis rata – rata logam
paduan itu.
Diket :
Logam A :m A = 0,04 kg dan  A= 8000 kg/ m3
Logam B :m B = 0,10 kg dan  B= 10000 kg
/m3
Ditanya : massa jenis rata – rata logam paduan

14. Jawab:
Massa total logam = mA + mB
= 0,04 + 0,10
= 0,14 kg
Volume total = VA + VB
=( mA / A) + (mB / B)
= (0,04/8000) + (0,10/10000)
= 0,6/40000
Maka
Massa jenis logam paduan = massa total :
volume total
= 0,14 : (0,6/40000)
= 9333 kg /m3

15. Hukum Pascal
 Tekanan yang di berikan kepada
fluida diam yang memenuhi
sebuah ruangan di teruskan oleh
fluida itu ke segala arah sama
besarnya.

16. Prinsip Hukum Pascal
F1
A1
F2
A2
Di rumuskan :
P1 = P2
(F1/A1) = (F2/A2)
Dengan :
F1 : gaya yang bekerja pd
piston 1
F2 : gaya yang bekerja pd
piston 2
A1 : luas penampang 1
A2 : luas penampang 2

17. Beberapa peralatan yang prinsip
kerjanya berdasarkan hkm. Pascal :
1. Dongkrak Hidrolik
2. Mesin Pres (Tekan)
Hidrolik
3. Pengangkat mobil hidrolik
4. Rem Hidrolik, dll

18. Dongkrak hidrolik
Pengangkat mobil hidrolik

19. Hukum Utama Hidrostatik
Di rumuskan :
P1 = P2
Po + 1gh1 = Po + 2gh2
1h1 = 2h2
Po
Po
1 2
h1
h2
Semua titik yang terletak pada suatu bidang datar di dalam zat
cair yang sejenis memiliki tekanan yang sama.

20. Contoh:
Sebuah bejana berhubungan diisi dengan
empat zat cair. Massa jenis zat cair itu
masing – masing :
1 = 1,2 gr/cm3, 2 = 8 gr/cm3
3 = 0,8 gr/cm3,
ho=10 cm , h1=20 cm, h2=24 cm, h3 = 12 cm
h4 = 18 cm
4 = …….?

21. Perhatikan gambar berikut:
Tentukan 4……….!
 1
 2
 4
 3
h2
h1
ho
h3
h4

22. Hukum Archimedes
• Memahami hkm Archimedes dengan
kajian eksperimen sederhana:
1. Siapkan sebuah beban, neraca pegas, gelas
ukur dan air secukupnya.
2. Masukan air dalam gelas ukur dan catat
volumenya (Vo)
3. Timbang beban dengan neraca pegas dan
catat beratnya (w1).
4. Masukkan beban yang masih tergantung pd
neraca pegas ke dalam gelas ukur yang berisi
air, catat volume air setelah dimasuki beban
(V1) dan berat beban dalam air (w2).
5. Hitung perbedaan volume air dan berat beban.
6. Bagaimana kesimpulannya

23. Gaya ke atas :
Maka di rumuskan :
Wbf = w – Fa
Fa = w – wbf
atau
Fa = F2 – F1
= P2 A – P1 A
= (P2 – P1)A
= f ghA
= (f g) (hbf A)
= (f g) Vbf
maka gaya ke atas di
rumuskan :
Fa = (f g) Vbf
Fa
W = mg
F2
F1

24. Fa
W = mg
F2
F1
Gaya ke atas
Di rumuskan :
Wbf = w – Fa
Fa = w – wbf
atau
Fa = F2 – F1
= P2 A – P1 A
= (P2 – P1)A
= f ghA
= (f g) (hbf A)
= (f g) Vbf
maka gaya ke atas di rumuskan :
Fa = (f g) Vbf

25. Dengan:
f = massa jenis fluida (kg/m3)
Vbf = volume benda dalam
fluida (m3)
Fa = gaya ke atas (N)

26. Jadi dapat di simpulkan :
• Suatu benda yang dicelupkan
seluruhnya atau sebagian ke
dalam fluida mengalami gaya
ke atas yang sama dengan
berat fluida yang dipindahkan

27. Contoh soal :
• Sebatang almunium digantung pada
seutas kawat. Kemudian seluruh
almunium di celupkan ke dalam
sebuah bejana berisi air. Massa
almunium 1 kg dan massa jenisnya
2,7 x 103 kg/m3. Hitung tegangan
kawat sebelum dan sesudah
almunium di celupkan ke air.

28. Penyelesaian:
Sebelum di celupkan air:
Fy = 0
T1 – mg = 0
T1 = mg
T1 = 1 x10
T1 = 10 N
T1
mg

29. Sesudah dicelupkan :
Fy = 0
T2 + Fa – mg = 0
T2 = mg – Fa
T2 = 1 x 10 – Fa
T2 = 10 - Fa
mg
T2
Fa

30. Volume Al :
VAl = m / 
= 1 / (2,7 x 103)
Maka Fa = Val f g
= 3,7 N
Sehingga :
T2 = 10 – 3,7
= 6,3 N

31. Mengapung
Karena bendanya
seimbang, maka :
Fy = 0
Fa – w = 0
Fa = w
Fa = mb g
Fa = (b Vb) g
(f Vbf) g = (b Vb) g
b = (Vbf/Vb) f
w
Fa
hb
hbf
b f


32. Atau
b = (Vbf/Vb) f
= (A hbf / A hb) f
b = ( hbf / hb ) f
Dengan :
b = massa jenis benda (kg / m3)
f = masa jenis fluida (kg / m3)
hb = tinggi benda (m)
hbf = tinggi benda dalam fluida (m)

33. Kesimpulan :
Benda yang dicelupkan ke dalam
fluida akan mengapung, bila massa
jenis rata – rata benda lebih kecil
daripada massa jenis fluida.
Syarat benda mengapung :
b < f

34. Contoh :
Sebuah benda di celupkan
ke dalam alkohol ( massa
jenis = 0,9 gr/cm3). Hanya
1/3 bagian benda yang
muncul di permukaan
alkohol. Tentukan massa
jenis benda!
Diket :
f = 0,9 gr/cm3
Bagian yang muncul =( 1/3
)hb, sehingga :
hbf = hb –
(1/3)hb = (2/3)hb
Ditanya : Massa jenis benda
(b)
Jawab :
3
6
,
0
9
,
0
3
2
cm
g
b
b
b
b
f
b
bf
b
h
h
h
h








35. Melayang
Syarat benda melayang :
Fa = w
(f Vbf) g = (b Vb) g
(f Vb) g = (b Vb) g
f = b
Fa
w
b f
=

36. Kesimpulan :
Benda yang dicelupkan ke dalam
fluida akan melayang, bila massa
jenis rata – rata benda sama dengan
massa jenis fluida.
Syarat benda melayang:
b = f

37. Contoh :
Sebuah balok kayu yang massa jenisnya 800 kg/m3 terapung
di air. Selembar aluminium yang massanya 54 gram dan
massa jenisnya 2700 kg/m3 diikatkan di atas kayu itu
sehingga sistem ini melayang. Tentukan volume kayu itu !
Diket :
kayu
aluminium
wk wAl
Fak
FaAl

38. Di tanya : volume kayu (Vk)
Jawab :
F = 0
Fak + FaAl – wk – wAl = 0
Fak + FaAl = wk + wAl
f g Vk + f g VAl = mkg + mAlg
f Vk + f VAl = mk + mAl
f Vk + f (mAl/ Al) = k Vk+ mAl
1 Vk + 1 (54/2,7) = 0,8 Vk + 54
Vk + 20 = 0,8 Vk + 54
Vk = 170 cm3

39. Tenggelam
Dengan cara yang sama
di peroleh :
b > f
Kesimpulan :
Benda yang
dicelupkan ke dalam
fluida akan tenggelam,
bila massa jenis rata –
rata benda lebih besar
daripada massa jenis
fluida.
w
Fa

40. Tantangan :
Sebuah balok mempunyai luas
penampang A, tinggi l, dan massa
jenis . Balok ada pd keseimbangan
di antara dua jenis fluida dengan
massa jenis 1 dan 2 dengan 1 <  <
2 .Fluida – fluida itu tidak bercampur.
Buktikan : Fa = [1gy + 2 g(l – y)]A
Buktikan :  = [1y + 2 (l – y)]/l

41. Ini gambarnya!
2
1

y
l

42. TEGANGAN PERMUKAAN
• CONTOH:

43. Contoh :
 Silet dapat mengapung di air
 Nyamuk dapat hinggap di atas air
Secara matematis tegangan permukaan di
rumuskan :
l
F


Dengan:
F : gaya (N)
l : panjang (m)
 ; tegangan permukaan (N/m)

44. Atau
Di rumuskan :
A
W


Dengan :
W = usaha (J)
A = luas penampang (m2)
 = tegangan permukaan (J/m2)

45. Tegangan permukaan pd sebuah bola




cos
cos
l
F
l
F
y
y


Dari gambar di
peroleh :
Karena
maka :
r
l 
2

Fy = 2  r  cos 

46. Contoh :
Seekor serangga berada di atas
permukaan air. Telapak kaki
serangga tersebut dapat di anggap
sebagai bola kecil dengan jari – jari 3
x 10-5 m. Berat serangga adalah 4,5 x
10-5 N dan tubuhnya di sangga oleh
empat buah kaki. Tentukan sudut
yang dibentuk kaki serangga dengan
bidang vertikal.

47. Diket :
r = 3 x 10-5 m
w = 4,5 x 10-5 N
n = 4
 = 0,072 Nm-1
Ditanya : 

48. Penyelesaian
0
5
5
33
83
,
0
cos
4
.
072
,
0
.
10
.
3
.
14
,
3
.
2
10
.
5
,
4
cos
2
cos
cos
2
cos
2




















n
r
w
r
n
w
r
Fy

49. Diskusi dan interaksi
Mengapa deterjen sering digunakan
untuk mencuci pakaian agar pakaian
menjadi bersih ?

50. Meniskus
Adalah bentuk cembung atau cekung
permukaan zat cair akibat tegangan
permukaan.
air Raksa



51. Proses pembentukan meniskus cekung
dan cembung
Adhesi adalah gaya tarik-menarik
antara partikel tak sejenis.
Kohesi adalah gaya tarik-menarik
antara partikel sejenis.

52. Perhatiakan gambar berikut:
Air Raksa

Fa
Fk
FR
Fa
Fk
FR


53. Kapilaritas :
Adalah peristiwa naik turunnya
permukaan zat cair di dalam pipa
kapiler.
Contoh :
peristiwa naiknya minyak tanah pd
sumbu kompor.
Air pd tanaman sampai ke daun
Dan lain-lain.

54. Perhatikan gambar berikut :
Air Raksa
y


water
y


mercury