The document discusses key concepts in fluid mechanics including: 1. Pressure is defined as force per unit area and its units are Pascal (SI) or dynes/cm2 (CGS). Atmospheric pressure at sea level is 101,325 Pa. 2. Density is defined as mass per unit volume and has units of kg/m3 (SI) or g/cc (CGS). Specific weight is weight per unit volume and specific gravity is the ratio of a fluid's density to that of water. 3. Viscosity describes a fluid's resistance to flow and is measured by dynamic viscosity in N·s/m2 or kinematic viscosity in m2/s.

1. MECHANICAL ENGINEERING – FLUIDMECHANICS
2
Pressure (P):
• If F be the normal force acting on a surface of area A in contact with liquid,then
pressure exerted by liquid on this surface is: P =F / A
• Units : N /m2 or Pascal (S.I.) and Dyne/cm2 (C.G.S.)
• Dimension
:
[P] =
[F]
[A]
=
[MLT 2 ]
[L2 ]
=[ML-1T -2
]
• Atmospheric pressure:Its value on the surface of the earth at sea level is nearly
1.01*10 5N/ m2 or Pascal in S.I. other practical units of pressure are atmosphere,
bar and torr (mm of Hg)
• 1atm = 1.01 *10 5Pa = 1.01bar = 760 torr
• Fluid Pressure at aPoint:
Density ( ρ):
dp=
dF
dA
• In a fluid, at a point, density ρ is defined as: Mass/volume
• In case of homogenous isotropic substance, it has no directional properties, so is
a scalar.
• It has dimensions [ML-3] and S.I. unit kg/m3 while C.G.S. unit g/ccwith
1g / cc = 10 3kg / m 3
• Density of body = Density of substance
• Relative density or specific gravity which is defined
as:
RD
Densit
Density
of body
of water
Specific Weight ( w):
• It is defined as the weight per unit volume.
• Specific weight =
Weight
=
m.g
Volume Volume
Specific Gravity or Relative Density(s):
• It is the ratio of specific weight of fluid to the specific weight of a standard fluid.
Standard fluid is water in case of liquid and H2 or air in case of gas.
Specific gravity=
𝐷𝑒𝑛𝑠𝑖𝑡𝑦 𝑜𝑓 𝐹𝑙𝑢𝑖𝑑
𝐷𝑒𝑛𝑠𝑖𝑡𝑦 𝑜𝑓 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝐹𝑙𝑢𝑖𝑑
or
𝛾
𝛾𝑤
or
𝜌
𝜌𝑤
Where, 𝛾 Specific weight , and 𝜌
Density of water specific

2. MECHANICAL ENGINEERING – FLUIDMECHANICS
3
Specific Volume ( v):
• Specific volume of liquid is defined as volume per unit mass. It is also defined as the
reciprocal of specific density.
• Specific volume =1/Density
Newton’s Law of viscosity
• 𝜏 = 𝜇
𝑑𝑢
𝑑𝑦
Where 𝜏 = Shear Stress, 𝜇= Co-efficient of viscosity or absolute viscosity
𝑑𝑢
𝑑𝑦
= Rate of angular deformation or rate of change of shear strain
Dynamic Viscosity and kinematic viscosity
• Dynamic Viscosity- Resistance offered by fluid to flow
• Units are Ns/m2
or Kg/ms
• 1 poise= 0.1 Ns/m2
• Kinematic Viscosity =
𝐷𝑦𝑛𝑎𝑚𝑖𝑐 𝑉𝑖𝑠𝑐𝑜𝑠𝑖𝑡𝑦(𝜇)
𝑀𝑎𝑠𝑠 𝐷𝑒𝑛𝑠𝑖𝑡𝑦 (𝜌)
• 1 Stoke= c.m2
/s = 10-4
m2
/s
Bulk Modulus
• Bulk modulus K=
dP
−dV
V
• Compressibility (β) =
1
K = −dV
VdP
= dρ
ρdP
Where K= Bulk modulus of elasticity, ρ= Density and V= Specific volume
Surface Tension
• The cohesive forces between liquid molecules are responsible for the phenomenon known as surface
tension
• Unit N/m
• Pressure inside drop P =
4σ
d
• Pressure inside bubble P =
8σ
d
• Pressure inside jet P =
2σ
d
Where d= Diameter of drop, P= Gauge pressure and σ= Surface tension

3. MECHANICAL ENGINEERING – FLUIDMECHANICS
4
Capillary Action
• Height of water in capillary tube- 𝒉 =
𝟒𝝈𝑪𝒐𝒔𝜽
𝝆𝒈𝒅
ℎ=rise in capillary 𝜎= Surface tension of water
D= Diameter of tube
𝜃=Angle of contact between liquid and material
𝜃=<90o for water and glass and >90o for mercury and glass
Absolute Pressure
Hydrostatic law
𝒅𝑷
𝒅𝒉
= 𝝆𝒈
𝐖𝐡𝐞𝐫𝐞 𝛒 = 𝐃𝐞𝐧𝐬𝐢𝐭𝐲 𝐚𝐧𝐝 𝐠 = 𝐀𝐜𝐜𝐞𝐥𝐞𝐫𝐚𝐭𝐢𝐨𝐧 𝐝𝐮𝐞 𝐭𝐨 𝐠𝐫𝐚𝐯𝐢𝐭𝐲
Manometers
• Piezometers
A
p gh

=
abs atm gauge
abs atm vac
P P P
P P P
= +
= −

4. MECHANICAL ENGINEERING – FLUIDMECHANICS
5
• U-Tube Manometer
1 1 2 2
A m B
P s gh s gh h gs P
+ − − =
Where s1,s2 and sm are density of fluids in
manometer
Hydrostatic Forces on submerged bodies
• Vertical Planes
Total Force 𝐅 = 𝛒𝐠𝐀𝐡
̅
• Center of Pressure
𝒉∗
=
𝑰𝒈
𝑨𝒉
̅
+ 𝒉
̅
• Horizontal Surface
Total Force 𝐅 = 𝛒𝐠𝐀𝐡
̅
• Center of Pressure
𝒉∗
= 𝒙
̅

5. MECHANICAL ENGINEERING – FLUIDMECHANICS
6
• Forces on Inclined surface .
total C G
F gh A

= 
• Centre of pressure
𝒉∗
=
𝑰𝒈𝑺𝒊𝒏𝟐
𝜽
𝑨𝒉𝑪.𝑮
+ 𝒉𝑪.𝑮
• Curved Surface –
2 2
tan
R h v
v
h
F F F
F
F

= +
=
Vertical component of force Fv
Weight of the liquid supported by
the curved surface over it up to the
free liquid surface
Horizontal component of force
Fh
Total pressure force on the vertical
projected area of the curved
surface
Completely submerged and floating at the interface of two liquids
1 1 2 2
B
F gV gV
 
= +
Where 1
V and 2
V are volumes
Body floating in a liquid
2
2
B
F V

=

6. MECHANICAL ENGINEERING – FLUIDMECHANICS
7
Principal of floatation
• If the body weight is equal to the buoyant force, the body will float
B
Mg W F gV

= = =
Condition of stability
• Fully submerged body
Stable Equilibrium: G below B
Unstable Equilibrium: G above B
Neutral Equilibrium: G coincides with B
• Floating body
Stable Equilibrium: M above G
Unstable Equilibrium: M below G
Neutral Equilibrium: M coincides with G
Metacentric height (GM)
• Metacentre radius (BM)
I
BM
V
=
• Metacentric Height (GM)
GM BM BG
I
GM BG
V
= −
= −

7. MECHANICAL ENGINEERING – FLUIDMECHANICS
8
Where I= Second moment area about body surface vertical axis
V = Volume of water displaced
Time period of transverse oscillation of floating body
• 2 G
K
T
gGM

= KG= Least radius of gyration, GM=Meta- Centric Height
Continuity Equation
• ρ1A1V1 = ρ2A2V2
Where A,V are cross-section area of the flow and Velocity of flow respectively
For incompressible flow ρ=constant so
A1V1 = A2V2
Generalized differential Continuity Equation
•
𝑑𝜌
𝑑𝑡
+
𝑑(𝜌𝑢)
𝑑𝑥
+
𝑑(𝜌𝑣)
𝑑𝑦
+
𝑑(𝜌𝑤)
𝑑𝑧
= 0
Where u,v and w are the velocities in x,y,and z direction respectively
For steady incompressible two dimensional flow, ρ=constant and
𝑑𝜌
𝑑𝑡
= 0
𝑑𝑢
𝑑𝑥
+
𝑑𝑣
𝑑𝑦
= 0
Velocity and Acceleration of Fluid Particle
• Velo = ui
⃗ + vj
⃗ + wk
⃗⃗
• Acceleration in X-direction 𝑎𝑥 =
𝑑𝑢
𝑑𝑡
= 𝑢
𝑑𝑢
𝑑𝑥
+ 𝑣
𝑑𝑢
𝑑𝑦
+ 𝑤
𝑑𝑢
𝑑𝑧
+
𝑑𝑢
𝑑𝑡
Acceleration in Y-direction 𝑎𝑦 =
𝑑𝑣
𝑑𝑡
= 𝑢
𝑑𝑣
𝑑𝑥
+ 𝑣
𝑑𝑣
𝑑𝑦
+ 𝑤
𝑑𝑣
𝑑𝑧
+
𝑑𝑣
𝑑𝑡
Acceleration in Y-direction 𝑎𝑧 =
𝑑𝑤
𝑑𝑡
= 𝑢
𝑑𝑤
𝑑𝑥
+ 𝑣
𝑑𝑤
𝑑𝑦
+ 𝑤
𝑑𝑤
𝑑𝑧
+
𝑑𝑤
𝑑𝑡
For steady flow
𝑑𝑢
𝑑𝑡
=
𝑑𝑣
𝑑𝑡
=
𝑑𝑤
𝑑𝑡
= 0
𝑎 = √𝑎𝑥
2 + 𝑎𝑦
2 + 𝑎𝑤
2
Note- Local Acceleration due to increase in rate of velocity with respect to time at a point and
convective acceleration due to rate of change of position (
𝑑𝑢
𝑑𝑡
=
𝑑𝑣
𝑑𝑡
=
𝑑𝑤
𝑑𝑡
= 0)

8. MECHANICAL ENGINEERING – FLUIDMECHANICS
9
Rotational fluid
ωz =
1
2
(
∂V
∂x
−
∂U
∂y
)
Vortex flow
• Free Vortex V*r=Constant
• Forced Vortex V=r ω and 𝐻 =
𝜔2𝑟2
2𝑔
Velocity potential
• If ∅ is the velocity function, then
𝑢 = −
𝜕∅
𝜕𝑥
, v=−
𝜕∅
𝜕𝑦
, 𝑤 = −
𝜕∅
𝜕𝑧
• Polar direction
𝑢𝑟 = −
𝜕∅
𝜕𝑟
,𝑢𝜃 = −
1
𝑟
𝜕∅
𝜕𝜃
Stream Function
• If  is the Stream function , then
𝑢 = −
𝜕
𝜕𝑦
, v=
𝜕
𝜕𝑥
Equipotential line
• Condition for Equipotential line 𝑑∅ = 0
So
𝑑𝑦
𝑑𝑥
= −
𝑢
𝑣
Line of constant stream function
• Condition for constant stream function 0
d =
𝑑𝑦
𝑑𝑥
=
𝑣
𝑢
Relation between stream function and velocity potential function
•
∂∅
∂x
=
∂
∂y
,
∂∅
∂y
= −
∂
∂x
Equation of motion
• 𝐹
𝑥 = 𝐹
𝑔 + 𝐹𝑃 + 𝐹
𝛾 + 𝐹𝑡 + 𝐹𝐶
Where,
Gravity force 𝐹
𝑔

9. MECHANICAL ENGINEERING – FLUIDMECHANICS
10
Pressure force 𝐹𝑃
Viscosity force 𝐹
𝛾
Turbulance force 𝐹𝑡
Compressibility force 𝐹𝐶
• When Compressibility force 𝐹𝐶 is negligible
𝐹
𝑥 = 𝐹
𝑔 + 𝐹𝑃 + 𝐹
𝛾 + 𝐹𝑡 is Reynold’s equation of motion
• 𝐹𝑡 is negligible
𝐹
𝑥 = 𝐹
𝑔 + 𝐹𝑃 + 𝐹
𝛾 is Navier- Stokes equation of motion
• When flow is assumed to be ideal, 𝐹
𝛾 = 0
𝐹
𝑥 = 𝐹
𝑔 + 𝐹𝑃 is Euler’s equation of motion
Euler’s equation of motion
•
𝑑𝑝
𝜌
+ 𝑔𝑑𝑧 + 𝑣𝑑𝑣 = 0
Bernoulli’s equation
• 𝑃 + 𝜌𝑔𝑧 +
𝜌𝑉2
2
= 0
•
P
ρg
+ z +
V2
2g
= 0
Where,
P
ρg
= Pressure head
Z = Potential head
V2
2g
= Kinetic head
Application of Bernoulli’s theorem
• Venturimeter
Qact = Cd
a1a2√2gh
√a1
2 − a2
2
Where,
Cd=Co-efficient of venturimeter which is <1
a1, a2= Area of cross section, h= Head
• Orifice meter
Vena contracta 𝐶𝑐 =
Area of vena contracta
Area of orific

10. MECHANICAL ENGINEERING – FLUIDMECHANICS
11
Discharge 𝐶𝑑 = 𝐶𝑐
√1−(
ao
a1
)
2
√1−(
ao
a1
)
2
𝑐𝑐
2
where,
a1= area of cross section before vena contracta
ao=Area of orifice
• Pitot Tube
𝐕𝐚𝐜𝐭 = 𝐂𝐯√𝟐𝐠(𝐒𝐭𝐚𝐠𝐧𝐚𝐭𝐢𝐨𝐧 𝐡𝐞𝐚𝐝 − 𝐒𝐭𝐚𝐭𝐢𝐜 𝐡𝐞𝐚𝐝)
Where 𝐂𝐯 is co-efficient of velocity
Value of 𝒉𝒑 given by differential
• 𝒉𝒑 = 𝒚(
𝑺𝒎
𝑺
− 𝟏) where 𝑺𝒎 > 𝑺
• 𝒉𝒑 = 𝒚(𝟏 −
𝑺𝒎
𝑺
) where S > 𝑺𝒎
𝑺𝒎, 𝑺 are realtive density of
manometric fluid and fluid flowing
Momentum Equation
• F.dt= d(mv) known as impulse- momentum equation
Force exerted on flowing fluid by a bend pipe
• If 𝜌1 = 𝜌2 then net force acting on a fluid
• 𝑃1𝐴1 − 𝑃1𝐴1𝐶𝑜𝑠𝜃 − 𝐹
𝑥 =
Change in velocity in horizontal ∗ mass of fluid
• Fy = ρQ(change in velocity vertically) − P2A2Sinθ
• Resultant force = √Fx
𝟐 + Fx
𝟐
Viscous flow
• To be viscous flow Reynold number should be less than 2000
𝑅𝑒 =
𝐼𝑛𝑒𝑟𝑡𝑖𝑎 𝑓𝑜𝑟𝑐𝑒
𝑉𝑖𝑠𝑐𝑜𝑢𝑠 𝑓𝑜𝑟𝑐𝑒
=
𝜌𝑉𝐷
𝜇
<2000
Where, v=velocity of flow, 𝜇= viscosity of flow, D= Diameter of piper and 𝜌= Density of fluid
• Flow of viscous fluid through circular pipe

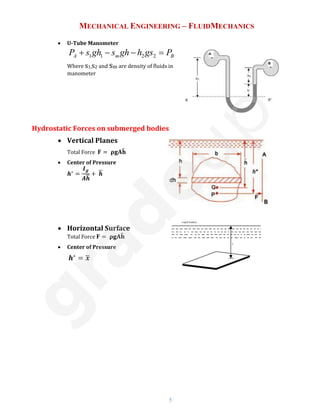
11. MECHANICAL ENGINEERING – FLUIDMECHANICS
12
➢ Velocity u =
1
4μ
(−
∂P
∂x
) [R2
− r2]
➢ Shear stress 𝜏 = (−
∂P
∂x
)
r
2
➢ Ratio of maximum to average velocity
Maximum Velocity
Average Velocity
= 2
➢ Drop of pressure in given length
P1 − P2
ρg
= hf =
32u
̅μL
ρgD2
Also called Hagen Poiseuille Equation
Here u
̅=average velocity, P1, P2 = Pressure at two different points in the pipe
• Flow of viscous fluid between two parallel plates
➢ Velocity u =
1
2μ
(−
∂P
∂x
) [ty − y2]
➢ Shear Stress 𝜏 =
1
2
(−
∂P
∂x
) [t − 2y]
➢ Ratio of maximum to average velocity
Maximum Velocity
Average Velocity
=
3
2
➢ Drop of pressure in given length
P1−P2
ρg
= hf =
12u
̅μL
ρgt2
Kinetic energy correction factor
α =
K.E
sec
based on actual velocity
K.E
sec
based on average velocity
For laminar flow α=2 and for turbulent flow α=1.33
Momentum correction factor
β =
Momentum
sec
based on actual velocity
Momentum
sec
based on average velocity
For laminar flow β=1.33 and for turbulent flow β=1.20
Loss of head due to friction in viscous flow
hf =
4flV2
2Dg
Where t is the thickness

12. MECHANICAL ENGINEERING – FLUIDMECHANICS
13
Where f= friction co-efficient
For laminar flow 𝑓 =
16
𝑅𝑒
where Re is Reynold’s number
For turbulent flow, coefficient of friction f =
0.079
Re
1
4
Chezy’s Formula
V = C√mi , C = Chezy Constant = √
ρg
f
i = Loss of head per unit length of pipe=
ℎ𝑓
𝐿
(hydraulic slope tan θ)
m = Hydraulic mean depth
Mean velocity of flow m =
Area (A)
Wetted Perimeter(P)
Minor losses in pipe
• Loss of head due to sudden enlargement
he =
(V1 − V1)2
2g
• Loss of head due to sudden contraction
he =
V2
2g
(
1
Cc
− 1)
2
or he = 0.5
V2
2g
when Cc=0.65
• Loss of head due to entrance
𝒉𝒆𝒏𝒕𝒓𝒂𝒏𝒄𝒆 = 0.5
V2
2g
• Loss due to exit pipe
=
𝑽𝟐
𝟐𝒈
• Loss due to obstruction
=
V2
2g
(
A
Cc(A−a)
− 1)
2
• Losses due to bend
= K
𝑽𝟐
𝟐𝒈
where k depends on bending of pipe
Hydraulic gradient and Total Energy line
• H.G.L=Pressure head+datum head
• T.G.L= Pressure head+datum head+Kinetic Head

13. MECHANICAL ENGINEERING – FLUIDMECHANICS
14
Flow through pipes in series or compound pipes
Major loss = Head loss due to friction in each pipe
While, minor loss = Entrance loss + Expansion loss +
Contraction loss + Exit loss
Flow will remain constant
Equivalent pipe in series pipe
𝐿
𝑑5
=
𝐿1
𝑑1
5 +
𝐿2
𝑑2
5 +
𝐿3
𝑑3
5
Power Transmission through pipes
• P =
ρgAV
1000
(H − hf)
hf = loss due to friction
• Efficency of power transmission
 =
𝑃𝑜𝑤𝑒𝑟 𝑎𝑣𝑎𝑖𝑙𝑎𝑏𝑙𝑒 𝑎𝑡 𝑜𝑢𝑡𝑙𝑒𝑡
𝑃𝑜𝑤𝑒𝑟 𝑠𝑢𝑝𝑝𝑙𝑖𝑒𝑑
=
𝐻−ℎ𝑓
𝐻
• Condition for maximum transmission of power
𝐻 = 3ℎ𝑓 and  = 66%
Dimensional analysis:
Quantity Symbol Dimensio
ns
Mass m M
Length l L
Time t T
Temperature T θ
Velocity u LT -1

14. MECHANICAL ENGINEERING – FLUIDMECHANICS
15
Acceleration a LT -2
Momentum/Impulse mv MLT -1
Force F MLT -2
Energy - Work W ML 2T -2
Power P ML 2T -3
Moment of Force M ML 2T -2
Angular momentum - ML 2T -1
Angle η M 0L 0T 0
Angular Velocity ω T -1
Angular acceleration α T -2
Area A L 2
Volume V L 3
First Moment of Area Ar L 3
Second Moment of Area I L 4
Density ρ ML -3
Specific heat-
Constant
Pressure
C p L 2 T -2 θ -1
Elastic Modulus E ML -1T -2
Flexural Rigidity EI ML 3T -2
Shear Modulus G ML -1T -2
Torsional rigidity GJ ML 3T -2
Stiffness k MT -2
Angular stiffness T/η ML 2
T -2
Flexibiity 1/k M -1
T 2
Vorticity - T -1
Circulation - L 2
T -1
Viscosity μ ML -1
T -1
Kinematic Viscosity τ L 2
T -1
Diffusivity - L 2
T -1
Friction coefficient f /μ M 0
L 0
T 0
Restitution coefficient M 0
L 0
T 0
Specific heat-
Constant volume
C v
L 2
T-2
θ -1

15. MECHANICAL ENGINEERING – FLUIDMECHANICS
16
Dimensionless number
• Reynold’s number (Re)
𝑅𝑒 =
𝐼𝑛𝑒𝑟𝑡𝑖𝑎𝑙 𝐹𝑜𝑟𝑐𝑒
𝑉𝑖𝑠𝑐𝑜𝑢𝑠 𝐹𝑜𝑟𝑐𝑒
=
𝜌𝑉𝐷
𝜇
• Froude’s Number (Fe)
Fe = √
Inertia Force
Gravity Force
=
𝑉
√𝐿𝑔
• Euler’s Equation (Eu)
𝐸𝑢 = √
𝐼𝑛𝑒𝑟𝑡𝑖𝑎 𝐹𝑜𝑟𝑐𝑒
𝑃𝑟𝑒𝑠𝑠𝑢𝑟𝑒 𝐹𝑜𝑟𝑐𝑒
=
𝑉
√𝑃
𝜌
⁄
• Weber’s number (We)
𝑊𝑒 =
𝐼𝑛𝑒𝑟𝑡𝑖𝑎 𝐹𝑜𝑟𝑐𝑒
𝑆𝑢𝑟𝑓𝑎𝑐𝑒 𝐹𝑜𝑟𝑐𝑒
=
𝑉
√𝜎
𝜌𝐿
⁄
• Mach number (M)
𝑀 =
𝐼𝑛𝑒𝑟𝑡𝑖𝑎
𝐸𝑙𝑎𝑠𝑡𝑖𝑐 𝐹𝑜𝑟𝑐𝑒
=
𝑉
𝐶
Velocity distribution for turbulent flow in pipe
v = vmax + 2.5V∗
loge (
Y
R
)
Where V∗
=√
𝜏𝑜
𝜌
Shear or friction velocity, Y=distance from pipe wall, 𝜌=Density
Displacement Thickness (𝛅∗
)
𝛅∗
= ∫ {1 −
𝑢
𝑈
} 𝑑𝑦
𝛿
0
U=Stream Velocity, u=Velocity of fluid at the element, δ= boundary layer thickness
Momentum Thickness (θ)
θ = ∫
𝑢
𝑈
{1 −
𝑢
𝑈
} 𝑑𝑦
𝛿
0
Energy Thickness (𝛅∗∗
)
𝛅∗∗
= ∫
𝑢
𝑈
{1 −
𝑢2
𝑈2
} 𝑑𝑦
𝛿
0

16. MECHANICAL ENGINEERING – FLUIDMECHANICS
17
Drag force on a flat plate due to boundary layer
τo
ρU2
=
∂θ
∂x
Know as Von Karman momentum integral equation
Drag force on plate obtained by 𝐹𝐷 = ∫ ∆𝐹 = ∫ 𝜏𝑜
𝐿
0
𝑏𝑑𝑥 where, b if thickness of plate
Local (𝐂𝐃
∗
)and average (𝐂𝐃) co-efficient of drag
CD
∗
=
τ0
ρU2
2
⁄
, CD =
τ0
ρAU2
2
⁄
Boundary condition for the velocity profile
• At y=0, u=0
• At y=𝛿, u=U
𝜕𝑢
𝜕𝑦
= 0

17. MECHANICAL ENGINEERING – FLUIDMECHANICS
18
Saparation of boundary layer
Force exerted by jet on plate
• Force exerted by jet = mass of fluid striking per sec *
change in velocity =
ρa(V)*(V – 0)
=ρa(V)2
Force exerted by jet on inclined plate
• Fn=ρa(V)2 Sinθ
• Force component in X-direction = Fn Sinθ
• Force component in Y-direction = Fn Cosθ
Force exerted by jet on curved plate
• Fx=ρaV(V+V cosθ)
• Fy=ρaV(0-V sinθ)
Force exerted by jet on curved plate , moving with some velocity
• Fx=ρa(V-u)( (V-u)+ (V-u) cosθ)
• Fy=ρa(V-u)(0-(V-u) sinθ)

18. MECHANICAL ENGINEERING – FLUIDMECHANICS
19
Forced exerted by a jet on a hinged plate
• Sinθ =
ρaV2
w
Hydraulic Efficiency =
𝐏𝐨𝐰𝐞𝐫 𝐝𝐞𝐥𝐢𝐯𝐞𝐫𝐞𝐝 𝐭𝐨 𝐫𝐮𝐧𝐧𝐞𝐫
𝐏𝐨𝐰𝐞𝐫 𝐬𝐮𝐩𝐩𝐥𝐢𝐞𝐝 𝐭𝐨 𝐢𝐧𝐥𝐞𝐭
=
𝐑.𝐏
𝐖.𝐏
Mechanical Efficiency =
𝐏𝐨𝐰𝐞𝐫 𝐚𝐭 𝐭𝐡𝐞 𝐬𝐡𝐚𝐟𝐭 𝐨𝐟 𝐭𝐡𝐞 𝐭𝐮𝐫𝐛𝐢𝐧𝐞
𝐏𝐨𝐰𝐞𝐫 𝐝𝐞𝐥𝐢𝐯𝐞𝐫𝐞𝐝 𝐛𝐲 𝐰𝐚𝐭𝐞𝐫 𝐭𝐨 𝐭𝐡𝐞 𝐫𝐮𝐧𝐧𝐞𝐫
=
𝐒.𝐏
𝐑.𝐏
Volumetric Efficiency =
𝐕𝐨𝐥𝐮𝐦𝐞 𝐨𝐟 𝐰𝐚𝐭𝐞𝐫 𝐚𝐜𝐭𝐮𝐚𝐥𝐥𝐲 𝐬𝐭𝐫𝐢𝐤𝐢𝐧𝐠 𝐭𝐡𝐞 𝐫𝐮𝐧𝐧𝐞𝐫
𝐕𝐨𝐥𝐮𝐦𝐞 𝐨𝐟 𝐰𝐚𝐭𝐞𝐫 𝐬𝐮𝐩𝐩𝐥𝐢𝐞𝐝 𝐭𝐨 𝐭𝐡𝐞 𝐭𝐮𝐫𝐛𝐢𝐧𝐞
Overall Efficiency =
𝐒𝐡𝐚𝐟𝐭 𝐏𝐨𝐰𝐞𝐫
𝐖𝐚𝐭𝐞𝐫 𝐏𝐨𝐰𝐞𝐫
= Hydraulic Efficiency * Mechanical Efficiency

19. MECHANICAL ENGINEERING – FLUIDMECHANICS
20
Work done by Pelton turbine
• Work 𝑊 = 𝜌𝑎𝑉1[𝑉𝜔1 − 𝑉𝜔2]𝑢 where 𝑉𝜔1, 𝑉𝜔2are whirl velocity
Hydraulic Efficiency
• Hydraulic Efficiency =
𝟐[𝐕𝛚𝟏±𝐕𝛚𝟐]𝐮
𝐕𝟏
𝟐
• When blade velocity= (inlet velocity of jet)/2 then,
Maximum efficiency
𝟏+𝑪𝒐𝒔∅
𝟐
Degree of reaction
R =
Change of pressure energy inside the runner
Change in total energy
Specific Speed
• For turbine 𝑁𝑠 =
𝑁√𝑃
𝐻
5
4
⁄
where P= power, H= head and N= number of rotation
• Dimensionless Specific speed 𝑁𝑠 =
𝑁√𝑃
(𝑔𝐻)
5
4
⁄
Turbine Specific Speed
(S.I)
Specific Speed
(M.K.S)
Pelton 8.5 to 30 10 to 35
Pelton with two jets 30 to 51 35 to 60
Francis 51 to 255 60 to 300
Kaplan and propeller 255 to 860 300 to 1000
For Pumps, 𝑁𝑠 =
𝑁√𝑄
𝐻
3
4
⁄
where Q is discharge
Unit quantities
• Unit speed (Nu): N = Nu√H
• Unit Power (Pu): P = Pu ∗ H
3
2
⁄
• Unit discharge (Qu): Q = Qu√H
Model laws of turbine
•
𝑄
𝑁𝐷3 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡
•
𝑄
√𝐻𝐷2 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡

20. MECHANICAL ENGINEERING – FLUIDMECHANICS
21
•
𝐻
𝑁2𝐷2 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡
•
𝑃
𝑁3𝐷5 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡
•
𝑃
𝐻
3
2
⁄ 𝐷2
= 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡
Net Positive suction Head in pump
• NPSH= Pressure head + Static head - Vapor pressure head of your product – Friction head loss