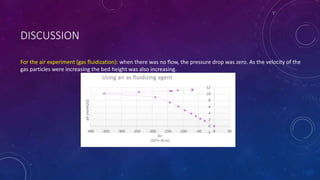
Fixed bed fluidization can be classified as particulate or bubbling, depending on if it occurs in liquids or gases. As gas velocity increases through a solid particle bed, drag forces counteract gravity and cause the bed to expand. At a critical velocity, particles are uniformly suspended and minimum fluidization occurs. Industrial applications include fluidized bed reactors and dryers where heat and mass transfer are improved over fixed beds. Experiments showed relationships between pressure drop and velocity confirm theoretical equations in both gas and liquid fluidization.

1. FIXED BED FLUIDIZATION
BY GROUP 1A

2. GROUP MEMBERS
NAMES INDEX NUMBER
ADJEI DENNIS OPOKU
8364119
AKUOKO STEPHEN 8365219
ASIGBE RITA BLESSING 8366919
KWABIA BOAHEMAA MENSAH 8368719
SEKE FELIX OPPONG 8371419
YORKE CLIFFORD 8372419

3. OUTLINE
• INTRODUCTION
• TYPES
• THEORY
• PROCESS DESCRIPTION
• DISCUSSION
• INDUSTRIAL APPLICATION
• CONCLUSION

4. INTRODUCTION
• What Is Fluidization …….???
• The Operation by which Fine Solids are Transformed into Fluid-Like State, through Contact with the Gas
or Liquid.
• Fluidization refers to those Gas-Solids and Liquid-Solids system in which the solid phase is subjected to
behave more or less like a Fluid by the upwelling current of gas or liquid stream moving through the bed
of solid particles.

5. TYPES
• Fluidization can be broadly classified into particulate fluidization and bubbling fluidization.
• Particulate fluidization occurs in liquids like water.
• Bubbling fluidization occurs in gas-fluidized beds. Here, when the bed is fluidized, large pockets of gas,
free of particles, are seen to rise through the bed.

6. THEORY
Fluidization starts at a point when the bed
• pressure drop exactly balances the net downward forces (gravity minus buoyancy forces) on the bed
packing. The first one is Ergun’s equation.
∆p/L = (1-Ꜫ)(Ꝭs- Ꝭ)g 1
∆𝑃
𝑙
=
150 . 𝜇𝑓 . 𝑣0 . (1 − ɛ)2
𝐷𝑝2 . ɛ3 +
1.75 . 𝜌𝑓 . 𝑣0
2
. (1 − ɛ)2
𝐷𝑝2 . ɛ3
• For fluidized beds, the following equation is used:
∆𝑃
𝑙
= 1 − ɛ . 𝜌𝑝 − 𝜌𝑓 . 𝑔

7. THE CARMAN-KOZENY EQUATION
• Carman modeled the bed as any small capillary tubes of diameter making up a bed of cross sectional
area. The equation was modified into
𝑑𝑃
𝑑𝑥
=
−180𝜇𝑢(1 − 𝜀)2
𝑑𝑠
2
𝜀3
where P = Pressure u = velocity
𝜇= viscosity ɛ = porosity

8. PROCESS DESCRIPTION
• When a gas flow is introduced through the bottom of a bed of solid particles, it will move upwards
through the bed via the empty spaces between the particles.
• At low gas velocities, aerodynamic drag on each particle is also low, and thus the bed remains in a fixed
state.
• Increasing the velocity, the aerodynamic drag forces will begin to counteract the gravitational forces,
causing the bed to expand in volume as the particles move away from each other.
• Further increasing the velocity, it will reach a critical value at which the upward drag forces will exactly
equal the downward gravitational forces, causing the particles to become suspended within the fluid.

9. • When trying to describe the operation of a fluidized bed, one main definition is the minimum
fluidization velocity.
• Another common characteristic of fluidized beds is the bed expansion.

10. DISCUSSION
For the air experiment (gas fluidization): when there was no flow, the pressure drop was zero. As the velocity of the
gas particles were increasing the bed height was also increasing.
-2
0
2
4
6
8
10
12
-400 -350 -300 -250 -200 -150 -100 -50 0 50
∆P
(mmH2O)
∆𝑥
(10^(−4) 𝑚)
Using air as fluidizing agent

11. DISCUSSION
For the water experiment (liquid fluidization): at a pressure head of zero, the bed had a height. From the experimented graph, as
the velocity was increasing, the head was increasing with an increase in the bed height till it reached a point where bed height
was increasing with a nearly constant pressure drop.
as the velocity was increasing, the head was increasing with an increase in the bed height till it reached a point where bed height
was increasing with a nearly constant pressure drop.
0
5
10
15
20
25
-350 -300 -250 -200 -150 -100 -50 0
∆P
(mmH2O)
∆𝑥
(10^(−4) 𝑚)
Using water as fluidizing agent

12. INDUSTRIAL APPLICATIONS

13. CONCLUSION
• Fluidization in air and water were compared in this study and the Carman Kozeny equation was also
verified in both currents. A linear relationship between pressure drop and velocity was recorded which
confirms the Carman- Kozeny equation. The minimum fluidization rate was also determined.
• Different fluids (in this case water and air) and bed particles are part of the main factors of fluidization.
The bed heights do not result in any significant change on the minimum fluidization velocity. However,
the bed height variations depend on the densities of the particles of the bed. Hence, the density
difference between the particle materials of the bed influences minimum fluidization velocity.
• A denser material requires a higher fluid velocity to start fluidization. Hence, the minimum fluidization
velocity increases when the density of the particles increases of the bed.

14. THANK YOU!