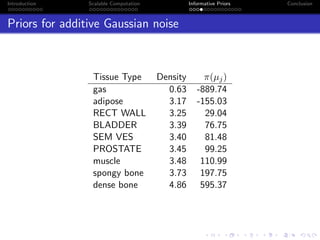
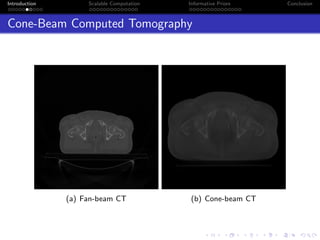
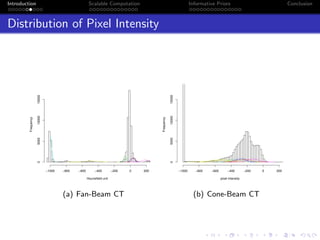
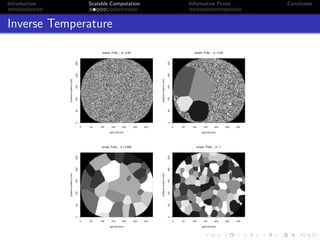
- The document summarizes Matthew Moores' PhD research on developing Bayesian computational methods for spatial analysis of medical and satellite images. - The objectives are to develop a generative image model incorporating prior information, implement it computationally efficiently, and apply it to radiotherapy and remote sensing data. - Challenges include intractable likelihoods, which are addressed through approximate Bayesian computation and sequential Monte Carlo with pre-computation. 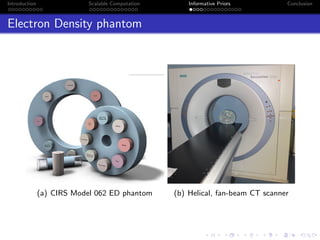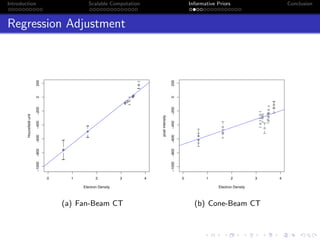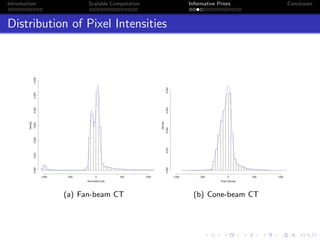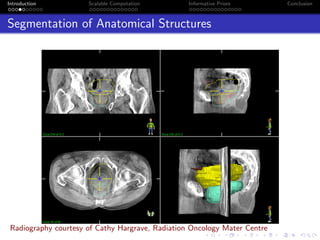- The research aims to classify pixels in medical and satellite images according to tissue type or land use by incorporating informative priors.

1. Introduction Scalable Computation Informative Priors Conclusion
Bayesian Computational Methods
for Spatial Analysis of Images
Matthew Moores
Mathematical Sciences School
Science & Engineering Faculty, QUT
PhD final seminar
August 1, 2014

2. Introduction Scalable Computation Informative Priors Conclusion
Acknowledgements
Principal supervisor: Kerrie Mengersen
Associate supervisor: Fiona Harden
Members of the Volume Analysis Tool project team at the
Radiation Oncology Mater Centre (ROMC), Queensland Health:
Cathy Hargrave
Mike Poulsen
Tim Deegan
QHealth ethics HREC/12/QPAH/475 and QUT ethics 1200000724
Other co-authors:
Chris Drovandi
Clair Alston
Christian Robert

3. Introduction Scalable Computation Informative Priors Conclusion
Outline
1 Introduction
Image-Guided Radiotherapy
Cone-Beam Computed Tomography
Aims & Objectives of the Thesis
2 Scalable Computation
Doubly-Intractable Likelihoods
Pre-computation for ABC-SMC
R package bayesImageS
3 Informative Priors
Informative Prior for µj and σ2
j
External Field
Experimental Results
4 Conclusion

4. Introduction Scalable Computation Informative Priors Conclusion
Objectives
The overall objectives of the research are:
to develop a generative model of a digital image that
incorporates prior information,
to produce a computationally efficient implementation of this
model, and
to apply the model to real world data in image-guided
radiotherapy and satellite remote sensing.
This reflects the parallel perspectives of statistical methods,
computational algorithms, and applied bio- and geo-statistics.

5. Introduction Scalable Computation Informative Priors Conclusion
Image-Guided Radiotherapy
Image courtesy of Varian Medical Systems, Inc. All rights reserved.

6. Introduction Scalable Computation Informative Priors Conclusion
Radiotherapy Process
Before Treatment
fan-beam
CT
MRI
contours
treatment
plan
QA

7. Introduction Scalable Computation Informative Priors Conclusion
Radiotherapy Process
Before Treatment
fan-beam
CT
MRI
contours
treatment
plan
QA
Daily Fractions (∼8 weeks)
position
patient
cone-beam
CT
deliver
dose
off-line
analysis

8. Introduction Scalable Computation Informative Priors Conclusion
Segmentation of Anatomical Structures
Radiography courtesy of Cathy Hargrave, Radiation Oncology Mater Centre

9. Introduction Scalable Computation Informative Priors Conclusion
Physiological Variability
Distribution of observed translations of the organs of interest:
Organ Ant-Post Sup-Inf Left-Right
prostate 0.1 ± 4.1mm −0.5 ± 2.9mm 0.2 ± 0.9mm
seminal vesicles 1.2 ± 7.3mm −0.7 ± 4.5mm −0.9 ± 1.9mm
Volume variations in the organs of interest:
Organ Volume Gas
rectum 35 − 140cm3 4 − 26%
bladder 120 − 381cm3
Frank, et al. (2008) Quantification of Prostate and Seminal Vesicle
Interfraction Variation During IMRT. IJROBP 71(3): 813–820.

10. Introduction Scalable Computation Informative Priors Conclusion
Cone-Beam Computed Tomography
(a) Fan-beam CT (b) Cone-beam CT

11. Introduction Scalable Computation Informative Priors Conclusion
Distribution of Pixel Intensity
Hounsfield unit
Frequency
−1000 −800 −600 −400 −200 0 200
050001000015000
(a) Fan-Beam CT
pixel intensity
Frequency
−1000 −800 −600 −400 −200 0 200050001000015000
(b) Cone-Beam CT

12. Introduction Scalable Computation Informative Priors Conclusion
Specific Aims I
The statistical aims of the research are:
M1 derivation and representation of informative priors for
the pixel labels.
M2 derivation of informative priors for additive Gaussian
noise from a previous image of the same subject.
M3 sequential Bayesian updating of this prior information
as more images are acquired.
The computational aims are:
C1 measuring the scalability of existing methods for
Bayesian inference with intractable likelihoods.
C2 development and implementation of improved
algorithms for fast, approximate inference in image
analysis.

13. Introduction Scalable Computation Informative Priors Conclusion
Specific Aims II
The applied aims are:
A1 To classify pixels in cone-beam CT scans of
radiotherapy patients according to tissue type.
A2 To demonstrate the broad applicability of these
methods by classifying pixels in satellite imagery
according to land use or abundance of phytoplankton.

14. Introduction Scalable Computation Informative Priors Conclusion
Research Progress
1 Moores, Hargrave, Harden & Mengersen (2014). Segmentation of
cone-beam CT using a hidden Markov random field with informative
priors. Journal of Physics: Conference Series 489:012076.
2 Moores & Mengersen (2014). Bayesian approaches to spatial inference:
modelling and computational challenges and solutions. To appear in AIP
Conference Proceedings.
3 Moores, Drovandi, Mengersen & Robert. Pre-processing for approximate
Bayesian computation in image analysis. Statistics & Computing
(Submitted: March 2014, Revised: June 2014).
4 Moores, Hargrave, Harden & Mengersen. An external field prior for the
hidden Potts model with application to cone-beam computed tomography.
Computational Statistics & Data Analysis (currently in revision).
5 Moores, Alston & Mengersen. Scalable Bayesian inference for the inverse
temperature of a hidden Potts model. (In Prep).
6 Moores, Hargrave, Deegan, Poulsen, Harden & Mengersen. Multi-object
segmentation of cone-beam CT using a hidden MRF with external field
prior. (In Prep).

15. Introduction Scalable Computation Informative Priors Conclusion
hidden Markov random field
Joint distribution of observed pixel intensities yi ∈ y
and latent labels zi ∈ z:
Pr(y, z|µ, σ2
, β) ∝ L(y|µ, σ2
, z)π(z|β) (1)
Additive Gaussian noise:
yi|zi =j
iid
∼ N µj, σ2
j (2)
Potts model:
π(zi|zi∼ , β) =
exp {β i∼ δ(zi, z )}
k
j=1 exp {β i∼ δ(j, z )}
(3)
Potts (1952) Proceedings of the Cambridge Philosophical Society 48(1)

16. Introduction Scalable Computation Informative Priors Conclusion
Inverse Temperature

17. Introduction Scalable Computation Informative Priors Conclusion
Doubly-intractable likelihood
p(β|z) = C(β)−1
π(β) exp {β S(z)} (4)
The normalising constant of the Potts model has computational
complexity of O(n2kn), since it involves a sum over all possible
combinations of the labels z ∈ Z:
C(β) =
z∈Z
exp {β S(z)} (5)
S(z) is the sufficient statistic of the Potts model:
S(z) =
i∼ ∈L
δ(zi, z ) (6)
where L is the set of all unique neighbour pairs.

18. Introduction Scalable Computation Informative Priors Conclusion
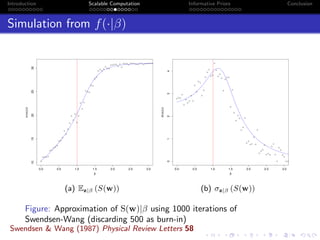
Expectation of S(z)
exact expectation of S(z) for n=12 and k=
β
E(S(z))
5
10
15
1 2 3 4
2
3
4
(a) n = 12 & k ∈ 2, 3, 4
exact expectation of S(z) for k=3 and n=
β
E(S(z))
5
10
15
1 2 3 4
4
6
9
12
(b) k = 3 & n ∈ 4, 6, 9, 12
Figure: Distribution of Ez|β[S(z)]

19. Introduction Scalable Computation Informative Priors Conclusion
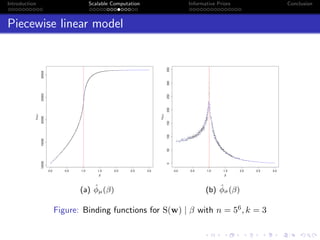
Standard deviation of S(z)
exact standard deviation of S(z) for n=12 and k=
β
σ(S(z))
0.0
0.5
1.0
1.5
2.0
2.5
3.0
1 2 3 4
2
3
4
(a) n = 12 & k ∈ 2, 3, 4
exact standard deviation of S(z) for k=3 and n=
β
σ(S(z))
0.0
0.5
1.0
1.5
2.0
2.5
1 2 3 4
4
6
9
12
(b) k = 3 & n ∈ 4, 6, 9, 12
Figure: Distribution of σz|β[S(z)]

20. Introduction Scalable Computation Informative Priors Conclusion
Approximate Bayesian Computation
Algorithm 1 ABC rejection sampler
1: for all iterations t ∈ 1 . . . T do
2: Draw independent proposal β ∼ π(β)
3: Generate w ∼ f(·|β )
4: if |S(w) − S(z)| < then
5: set βt ← β
6: else
7: set βt ← βt−1
8: end if
9: end for
Grelaud, Robert, Marin, Rodolphe & Taly (2009) Bayesian Analysis 4(2)
Marin & Robert (2014) Bayesian Essentials with R §8.3

21. Introduction Scalable Computation Informative Priors Conclusion
Pre-computation Step
The distribution of the summary statistics f(S(w)|β) is
independent of the observed data y
By simulating pseudo-data for values of β, we can create a
binding function φ(β) for an auxiliary model fA(S(w)|φ(β))
This binding function can be reused across multiple datasets,
amortising its computational cost
By replacing S(w) with approximate values drawn from our
auxiliary model, we avoid the need to simulate pseudo-data during
model fitting.
Wood (2010) Nature 466
Cabras, Castellanos & Ruli (2014) Metron (to appear)

22. Introduction Scalable Computation Informative Priors Conclusion
Simulation from f(·|β)
0.0 0.5 1.0 1.5 2.0 2.5 3.0
1015202530
β
E(S(z))
(a) Ez|β (S(w))
0.0 0.5 1.0 1.5 2.0 2.5 3.001234
β
σ(S(z))
(b) σz|β (S(w))
Figure: Approximation of S(w)|β using 1000 iterations of
Swendsen-Wang (discarding 500 as burn-in)
Swendsen & Wang (1987) Physical Review Letters 58

23. Introduction Scalable Computation Informative Priors Conclusion
Piecewise linear model
0.0 0.5 1.0 1.5 2.0 2.5 3.0
1000015000200002500030000
β
ES(z)
(a) ˆφµ(β)
0.0 0.5 1.0 1.5 2.0 2.5 3.0
050100150200250300350
β
σS(z)
(b) ˆφσ(β)
Figure: Binding functions for S(w) | β with n = 56
, k = 3

24. Introduction Scalable Computation Informative Priors Conclusion
Scalable ABC-SMC for the hidden Potts model
Algorithm 2 ABC-SMC using precomputed fA(S(w)|φ(β))
1: Draw N particles βi ∼ π0(β)
2: Draw N × M statistics ˆS(wi,m) ∼ N ˆφµ(βi), ˆφσ(βi)2
3: repeat
4: Update S(zt)|y, πt(β)
5: Adaptively select ABC tolerance t
6: Update importance weights ωi for each particle
7: if effective sample size (ESS) < Nmin then
8: Resample particles according to their weights
9: end if
10: Update particles using random walk proposal
(with adaptive RWMH bandwidth σ2
t )
11: until
naccept
N < 0.015 or t < 10−9 or t ≥ 100

25. Introduction Scalable Computation Informative Priors Conclusion
Accuracy of posterior estimates for β
0.2 0.4 0.6 0.8 1.0
0.00.20.40.60.81.0
β
posteriordistribution
(a) pseudo-data (M=50)
0.2 0.4 0.6 0.8 1.0
0.00.20.40.60.81.0
β
posteriordistribution
(b) pre-computed (M=200)

26. Introduction Scalable Computation Informative Priors Conclusion
Improvement in runtime
Pseudo−data Pre−computed
0.51.02.05.010.020.050.0100.0
algorithm
elapsedtime(hours)
(a) elapsed (wall clock) time
Pseudo−data Pre−computed
5102050100200500
algorithm
CPUtime(hours)
(b) CPU time

27. Introduction Scalable Computation Informative Priors Conclusion
bayesImageS
An R package for Bayesian image segmentation
using the hidden Potts model:
RcppArmadillo for fast computation in C++
OpenMP for parallelism
§
l i b r a r y ( bayesImageS )
p r i o r s ← l i s t ("k"=3,"mu"=rep (0 ,3) , "mu.sd"=sigma ,
"sigma"=sigma , "sigma.nu"=c (1 ,1 ,1) , "beta"=c (0 ,3))
mh ← l i s t ( algorithm="pseudo" , bandwidth =0.2)
r e s u l t ← mcmcPotts ( y , neigh , block ,NULL,
55000 ,5000 , p r i o r s ,mh)
Eddelbuettel & Sanderson (2014) RcppArmadillo: Accelerating R with
high-performance C++ linear algebra. CSDA 71

28. Introduction Scalable Computation Informative Priors Conclusion
Bayesian computational methods
bayesImageS supports methods for updating the latent labels z:
Chequerboard updating (Winkler 2003)
Swendsen-Wang (1987)
and also methods for updating the inverse temperature β:
Pseudolikelihood (Ryd´en & Titterington 1998)
Path Sampling (Gelman & Meng 1998)
Exchange Algorithm (Murray, Ghahramani & MacKay 2006)
Approximate Bayesian Computation (Grelaud et al. 2009)
Sequential Monte Carlo (ABC-SMC) with pre-computation
(Del Moral, Doucet & Jasra 2012; Moores et al. 2014)

29. Introduction Scalable Computation Informative Priors Conclusion
Electron Density phantom
(a) CIRS Model 062 ED phantom (b) Helical, fan-beam CT scanner

30. Introduction Scalable Computation Informative Priors Conclusion
Regression Adjustment
0 1 2 3 4
−1000−800−600−400−2000200
Electron Density
Hounsfieldunit
(a) Fan-Beam CT
0 1 2 3 4
−1000−800−600−400−2000200
Electron Density
pixelintensity
(b) Cone-Beam CT

31. Introduction Scalable Computation Informative Priors Conclusion
Distribution of Pixel Intensities
Hounsfield units
Density
−1000 −500 0 500 1000
0.0000.0010.0020.0030.0040.0050.006
(a) Fan-beam CT
Pixel intensity
Density
−1000 −500 0 500 1000
0.0000.0010.0020.0030.004
(b) Cone-beam CT

32. Introduction Scalable Computation Informative Priors Conclusion
Priors for additive Gaussian noise
Tissue Type Density π(µj)
gas 0.63 -889.74
adipose 3.17 -155.03
RECT WALL 3.25 29.04
BLADDER 3.39 76.75
SEM VES 3.40 81.48
PROSTATE 3.45 99.25
muscle 3.48 110.99
spongy bone 3.73 197.75
dense bone 4.86 595.37

33. Introduction Scalable Computation Informative Priors Conclusion
Treatment Plan
−50 0 50
150200250
right−left (mm)
posterior−anterior(mm)

34. Introduction Scalable Computation Informative Priors Conclusion
External Field
p(zi|zi∼ , β, µ, σ2
, yi) =
exp {αi,zi + π(αi,zi )}
k
j=1 exp {αi,j + π(αi,j)}
π(zi|zi∼ , β)
(7)
Isotropic translation:
π(αi,j) = log



1
nj
h∈j
φ ∆(h, i)|µ∆ = 1.2, σ2
∆ = 7.32



(8)
where
nj is the number of voxels in object j
h ∈ j are the voxels in object j
∆(u, v) is the Euclidean distance between the coordinates of
pixel u and pixel v
µ∆, σ2
∆ are parameters that describe the level of spatial
variability of the object j

35. Introduction Scalable Computation Informative Priors Conclusion
External Field II
External field prior for the ED phantom (σ∆ = 7.3mm)

36. Introduction Scalable Computation Informative Priors Conclusion
Anisotropy
αi(prostate) ∼ MVN




0.1
−0.5
0.2

 ,


4.12 0 0
0 2.92 0
0 0 0.92




(a) Bitmask (b) External Field

37. Introduction Scalable Computation Informative Priors Conclusion
Seminal Vesicles
αi(SV) ∼ MVN




1.2
−0.7
−0.9

 ,


7.32 0 0
0 4.52 0
0 0 1.92




(a) Bitmask (b) External Field

38. Introduction Scalable Computation Informative Priors Conclusion
External Field
Organ- and patient-specific external field (slice 49, 16mm Inf)

39. Introduction Scalable Computation Informative Priors Conclusion
Preliminary Results
−300 −250 −200 −150
150200250300
right−left (mm)
posterior−anterior(mm)
(a) Cone-Beam CT
−300 −250 −200 −150
150200250300
right−left (mm)
posterior−anterior(mm)
(b) Segmentation

40. Introduction Scalable Computation Informative Priors Conclusion
ED phantom experiment
27 cone-beam CT scans of the ED phantom
Cropped to 376 × 308 pixels and 23 slices
(330 × 270 × 46 mm)
Inner ring of inserts rotated by between 0◦ and 16◦
2D displacement of between 0mm and 25mm
Isotropic external field prior with σ∆ = 7.3mm
9 component Potts model
8 different tissue types, plus water-equivalent background
Priors for noise parameters estimated from 28 fan-beam CT
and 26 cone-beam CT scans

41. Introduction Scalable Computation Informative Priors Conclusion
Image Segmentation

42. Introduction Scalable Computation Informative Priors Conclusion
Quantification of Segmentation Accuracy
Dice similarity coefficient:
DSCg =
2 × |ˆg ∩ g|
|ˆg| + |g|
(9)
where
DSCg is the Dice similarity coefficient for label g
|ˆg| is the count of pixels that were classified with the
label g
|g| is the number of pixels that are known to truly
belong to component g
|ˆg ∩ g| is the count of pixels in g that were labeled correctly
Dice (1945) Measures of the amount of ecologic association between species.
Ecology 26(3): 297–302.

43. Introduction Scalable Computation Informative Priors Conclusion
Results
Tissue Type Simple Potts External Field
Lung (inhale) 0.507 ± 0.053 0.868 ± 0.011
Lung (exhale) 0.169 ± 0.006 0.839 ± 0.008
Adipose 0.048 ± 0.006 0.713 ± 0.041
Breast 0.057 ± 0.017 0.748 ± 0.007
Water 0.123 ± 0.134 0.954 ± 0.004
Muscle 0.071 ± 0.004 0.758 ± 0.016
Liver 0.075 ± 0.011 0.662 ± 0.033
Spongy Bone 0.094 ± 0.020 0.402 ± 0.175
Dense Bone 0.013 ± 0.001 0.297 ± 0.201
Table: Segmentation Accuracy (Dice Similarity Coefficient ±σ)

44. Introduction Scalable Computation Informative Priors Conclusion
Discussion
Contributions of this thesis:
M1 External field prior for representing spatial
information in the hidden Potts model
M2 Regression model for adjusting priors for the noise
parameters µj and σ2
j
C2 Pre-computation for ABC-SMC leads to two orders
of magnitude faster computation
A1 Application to cone-beam CT scans of the ED
phantom and radiotherapy patient data from the
Radiation Oncology Mater Centre
Not discussed in this talk:
M3 Sequential Bayesian updating of the external field
prior
C1 Scalability experiments with other algorithms for
doubly-intractable likelihoods
A2 Application to satellite remote sensing

45. Introduction Scalable Computation Informative Priors Conclusion
Ongoing & Future Work
Complete the analysis of the patient data and submit journal
article to ANZ J. Stat.
Model object boundaries (eg. for bony anatomy) and spatial
correlation between objects
Model spatially-correlated noise and artefacts in cone-beam
CT scans
Collaboration with Antonietta Mira & Alberto Caimo (USI,
Switzerland) on pre-computation for ERGM

46. ED phantom inserts
Tissue Type Electron Density Diameter
(×1023/cc) (cm)
Lung (inhale) 0.634 3.05
Lung (exhale) 1.632 3.05
Adipose 3.170 3.05
Breast 3.261 3.05
Water 3.340 *
Muscle 3.483 3.05
Liver 3.516 3.05
Spongy Bone 3.730 3.05
Dense Bone 4.862 1.00
Table: Properties of the CIRS Model 062 ED phantom
* overall dimensions are 33cm × 27cm × 5cm

47. Cone-beam CT reconstructed images
Half-fan acquisition mode: FOV 450mm × 450mm × 137mm
(Kan, Leung, Wong & Lam 2008)
reconstructed from 650-700 projections (Varian .HND files)
512 × 512 pixels with 2mm slice width (70-80 slices)
∼ 20 million voxels
70-80MB DICOM image stack