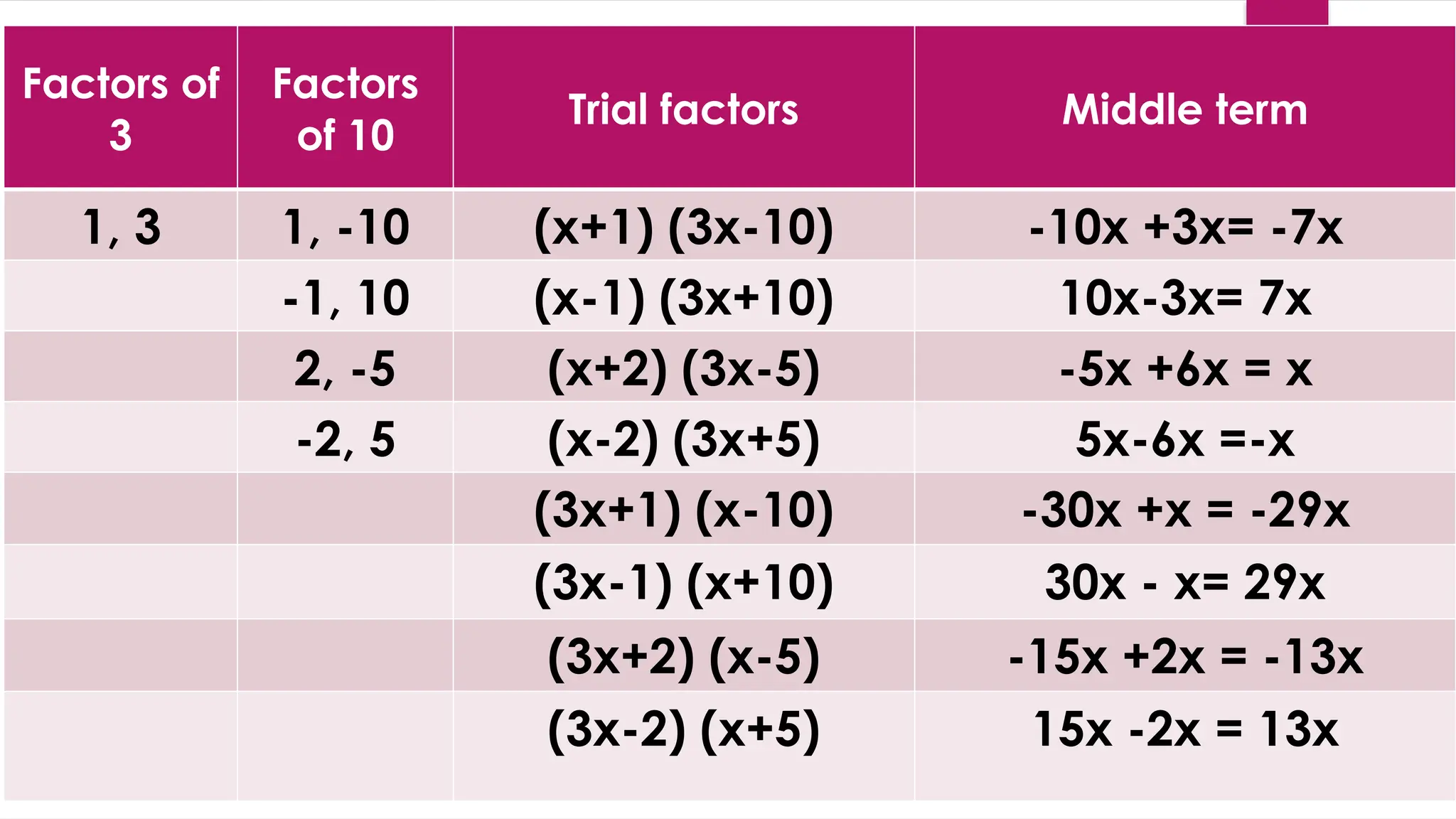
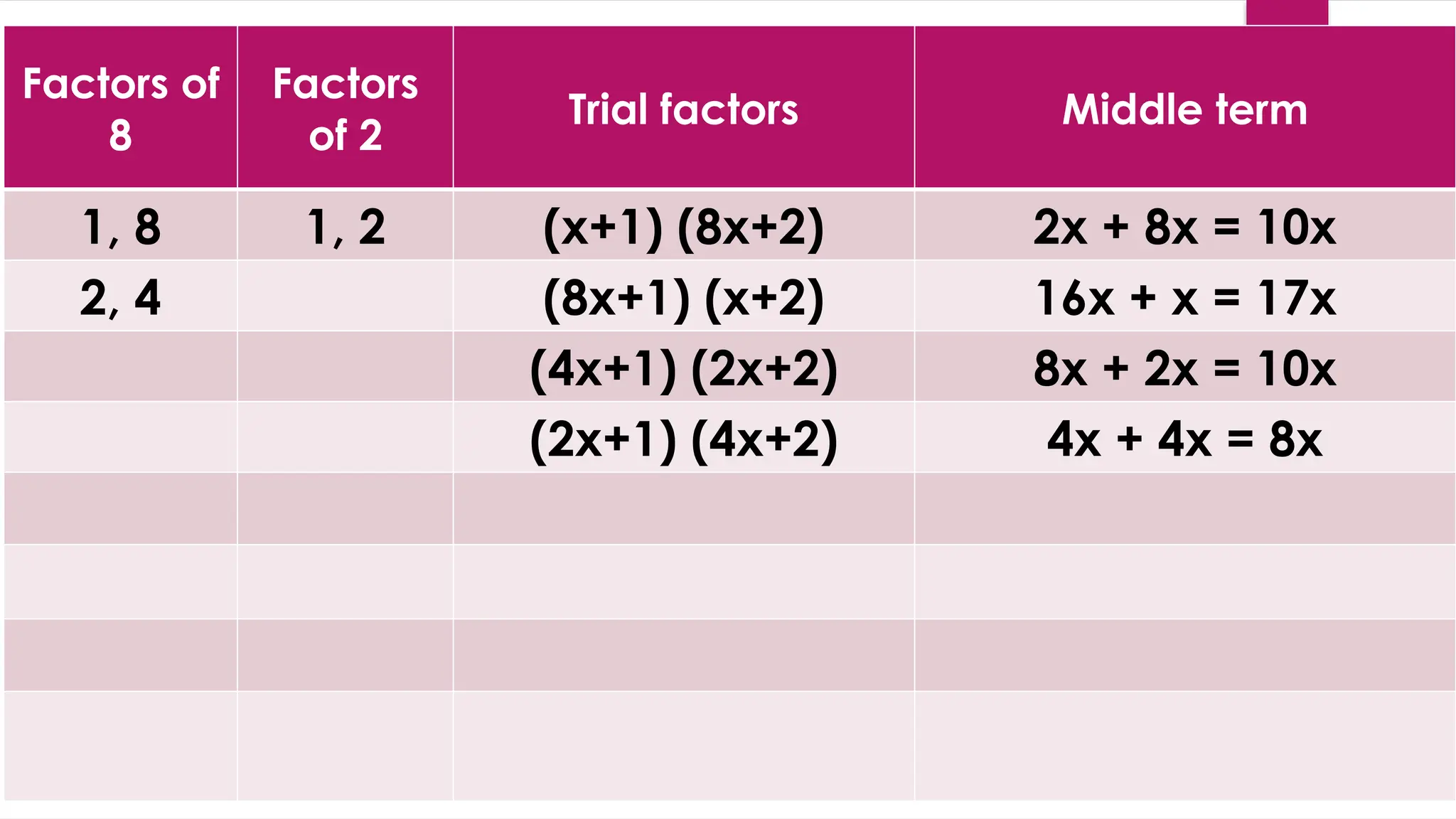
The document provides a comprehensive guide to factoring quadratic trinomials of the form ax² + bx + c, outlining objectives, methods, and examples. It covers techniques like the try, check, and revise method, illustrating how to find factors through various examples and exercises. Additionally, it includes assignments and quizzes to help reinforce the learning of factoring polynomials.

1. FACTORING
TRINOMIALS OF THE
FORM ax2
+ bx + c

2. Objectives
In this lesson, you will be able to:
1. factor general quadratic trinomials
completely; and
2. solve problems involving factors of
polynomials.

3. Extension
The quadratic trinomials in Exploration are of the form
ax2
+ bx +c with a 1.
In 2x2
+ 9x +4, a = 2, b = 9, and c = 4
In 6x2
+ 13x +6, a = 6, b = 13, and c = 6

4. Extension
The process of factoring
these trinomials involves the
try, check and revise
method

5. Example
Factor 9x2
+15x + 4

6. Step 1.
Find two factors such
that the product of the
first two terms is 9x2

7. Step 2.
The product of the last
two terms in each factor
must be 4.

8. Step 3
Write the factors of 4 together
with the factors of 9x2
.
Determine the middle term of
each product using FOIL
method.

9. Factors of 4
Possible factors of 9x2
+15x +4
Sum of outer terms and
Inner terms
1, 4 (9x + 1) (x+4) 36x + x = 37 x
4,1 (9x + 4) (x+1) 9x + 4x = 13x
2,2 (9x + 2) (x+2) 18x + 2x = 20x
1,4 (3x + 1) (3x+4) 12x +3x = 15x
2, 2 (3x + 2) (3x+2) 6x +6x =12x

10. Factor each completely.
a. 3x2
-x -10
b. 8x2
+17x +2
c. 2x2
-13x + 15
Example 2

11. Factors of
3
Factors
of 10
Trial factors Middle term
1, 3 1, -10 (x+1) (3x-10) -10x +3x= -7x
-1, 10 (x-1) (3x+10) 10x-3x= 7x
2, -5 (x+2) (3x-5) -5x +6x = x
-2, 5 (x-2) (3x+5) 5x-6x =-x
(3x+1) (x-10) -30x +x = -29x
(3x-1) (x+10) 30x - x= 29x
(3x+2) (x-5) -15x +2x = -13x
(3x-2) (x+5) 15x -2x = 13x

12. Factors of
8
Factors
of 2
Trial factors Middle term
1, 8 1, 2 (x+1) (8x+2) 2x + 8x = 10x
2, 4 (8x+1) (x+2) 16x + x = 17x
(4x+1) (2x+2) 8x + 2x = 10x
(2x+1) (4x+2) 4x + 4x = 8x

13. Assignment: Factor each completely
a. 2x2
-11x + 15
b. 5x2
-12x + 4

14. 1. Two of the terms must be
perfect squares, x2
and y2

15. 2. There must be no minus
sign before x2
and y2

16. 3. If you multiply x and y and
double the result, you get
the middle term

17. 4x2
+20x+25 = (2x)2
+ 2(2x)(5) +52
Example
(2x+5)2

18. Example 1
Factor each completely.
a. x2
+16x + 64
b. 9x2
-30xy + 25y2
c. x2
+5x + 6

19. Try it # 1
Which of the following are perfect square
trinomials
a. x2
+8x + 16
b. 4x2
-20xy + 25y2

20. Example 2
Factor each completely.
a. x2
+10x + 25
b. 16x2
-72x + 81
c. 25m2
+20mn + 4n2

21. Try it # 2
Factor each completely.
a. p2
+18p + 81
b. 9r2
-42r + 49

22. Example # 4
Factor each completely.
a. 4x3
-24x2
+ 36x
b. 27a2
-72ab + 48b2

23. Assignment
Find the length of a side(s)
of a square if its area (A) is
9x2
+ 30x +25
A=9x2
+30x+25

24. Quiz # 4
Factor each completely.
1. a2
-6a + 9
2. 1 +8c + 16c2
3. 64d2
-16d + 1

25. Quiz # 4 Factor each
completely.
4. a2
-6a + 9
5. 49g2
+56gh + 16h2
6. 9m2
-30mn + 25n2
7. 25p2
-60pq + 36q2