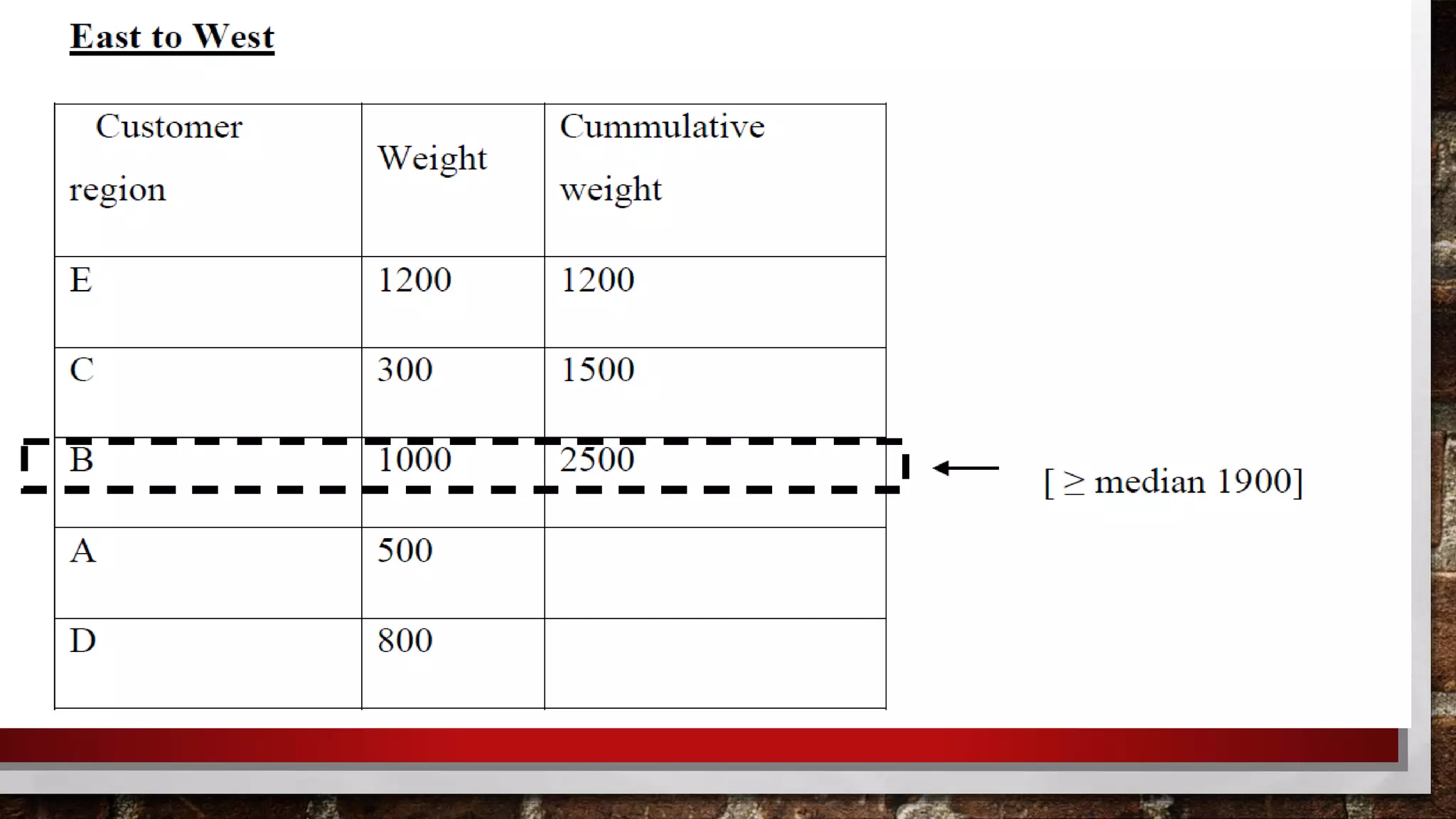
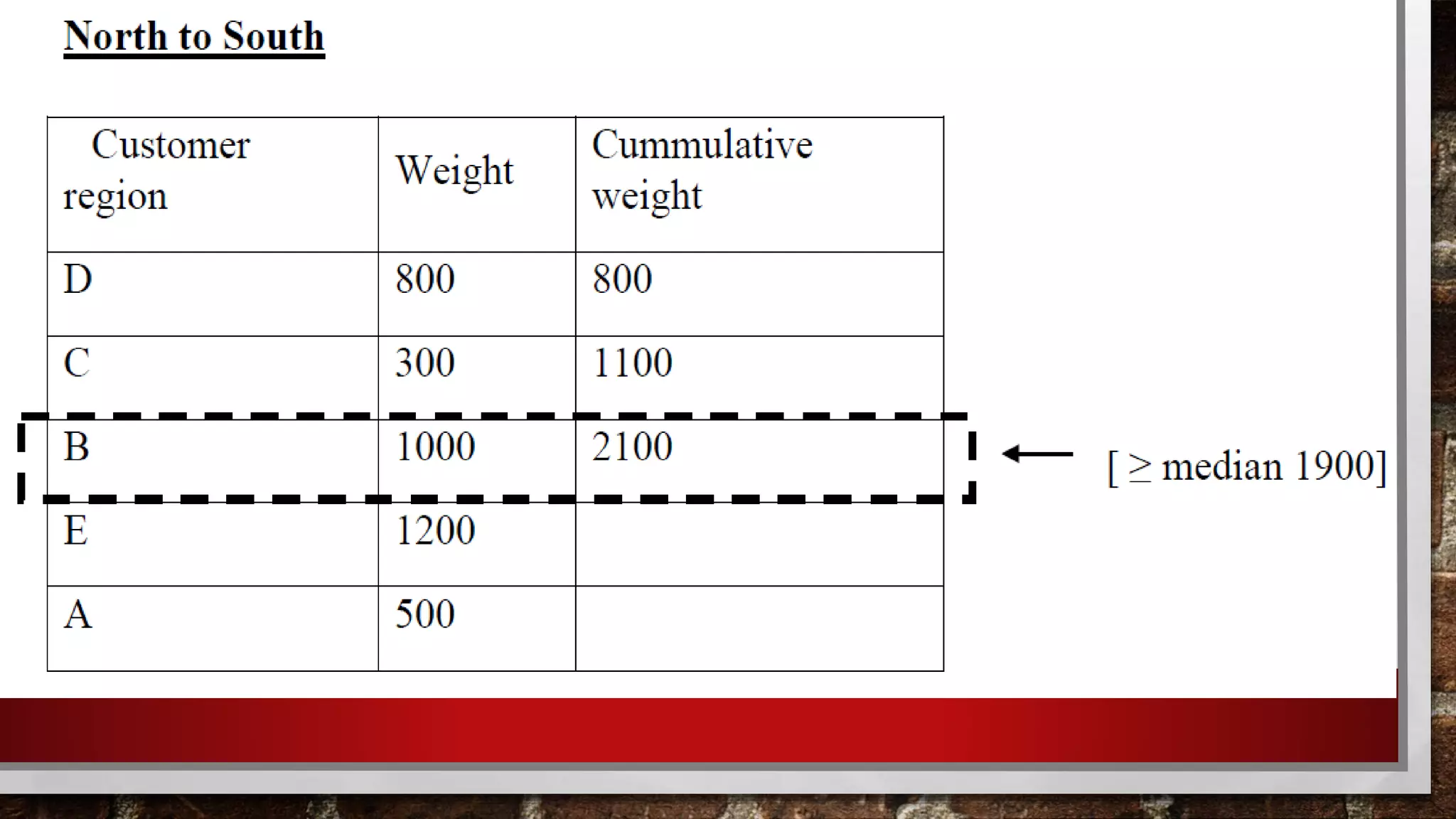
The document provides an overview of facility location planning, including quantitative methods and models used to determine optimal locations. It discusses factors that influence facility location such as market proximity, transportation, labor, and government policies. Location models addressed include single facility problems that aim to minimize maximum distance, and multiple facility problems formulated as set covering problems to minimize the number of facilities needed. Quantitative techniques include break-even analysis, center of gravity models, and solving location problems on lines and planes using median and gravity center approaches.

2. OVERVIEW
•Introduction
•Concept Of Facility Location
•Quantitative methods for facility location
•Break Even Analysis
•Facility location on a line and a plane
•Quantitative models for multiple service facilities

3. INTRODUCTION
•The Selection Of An Appropriate Plant Location And Layout Are The Two
Most Important Strategic Decisions Made By An Organization.
•Because The Overall Profitability Of An Organization Depends On The
Location And Layout Of Its Plant.
•Plant Location Refers To A Region Or Site Selected By An Organization
For Setting Up A Business Factory.

4. DEFINITION
•“The Function Of Determining Where The Plant Should Be Located For Maximum
Operating Economy And Effectiveness.”
- R.C Davis
•“That Spot Where, In Consideration Of Business As A Whole, The Total Cost Of
Production And Delivering Goods To All The Customers Is The Lowest.”
- Bethel Smiths & Atwater

5. CONCEPT OF FACILITY LOCATION
An organization may look for a new facility location for the following reasons:
•Commencement of a new business
•Obsolescence of the existing technology
•Expansion of the existing business
•Expiry of the lease agreement
•Reduction in overall costs

6. FACTORS AFFECTING A FACILITY LOCATION
•Market proximity
•Proximity to raw materials
•Availability of capital
•Availability of labour
•Transportation system
•Government policies
•Natural factors
•Availability of power

7. cntd.
Facility
location
planning
Availability of
power supply
Good
transportation
facilities
Residential
complexes,
schools,
hospitals, etc
Basic
amenities
Govt.
policies
Environmental
and
communityProximity to
sub
contractors
Easy
availability of
cheap land
Low
construction
costs
Proximity to
markets
Proximity
to raw
materials

8. LOCATING FOREIGN OPERATIONS FACILITIES
•Factors:
•Trade barriers
•International customers
•International competition
•Regulations
•Additional resources
•Lower costs
•Incentives

9. contd.
International
facility location
planning
Trade
Barriers
International
customers
Regulations
Additional
resources
Low
Costs
incentives
Economics of
scale
Power
and
prestige
Offensive in
competitor’s
home country
Synergy

10. FACTOR AND LOCATION RATING
•The importance of each factors discussed earlier may vary for
different types of plants.
•According to the requirements of a new plant, a set of these factors
is considered.
•These factors are rated from 1 to 5 indicate the importance attached
to them.These are called factor ratings.

11. contd.
•Now, with respect to each of the locations, we give each of these
factors another rating, called the location rating, according to the
benefits a particular location option offers.

14. EXAMPLE
• OBJECTIVE: GOVERNMENT OF ONE NATION WANTS TO OPEN UP HEALTH CHECK UP CLINIC IN A VILLAGE
• DECISION: WHERE TO LOCATE HEALTH CHECK UP CLINIC OUT OF THREE SITES; SITE1- NEAR BUS STOP,
SITE 2- CENTER OF THE VILLAGE, SITE 3– NEAR MANDI (VEGETABLE AND GROCERY MARKET)
• FACTOR TO BE CONSIDERED:
• 1. ACCESSIBILITY FOR ALL VILLAGERS
• 2. ANNUAL LEASE COST
• 3. DELIVERY OF MEDICINES

15. SOLUTION:

16. BREAK-EVEN ANALYSIS FOR FACILITY
LOCATION PLANNING
The conversion process from inputs to outputs involves two types of costs, namely,
• Fixed cost
• Variable cost

17. GRAPH

18. SINGLE FACILITY LOCATION PROBLEM: MINIMIZE MAXIMUM
DISTANCE
• THIS SET OF PROBLEMS USUALLY OCCURS TO MEET THE OBJECTIVE OF SOME PUBLIC SECTOR OR SOME
SOCIAL INITIATIVE.
• MOST OF SUCH FACILITIES CAN BE EMERGENCY HOSPITAL SERVICES, LOCATION OF AMBULANCE STAND
AND LOCATION OF FIRE STATION.
• THE MAIN AIM OF SUCH SERVICES IS TO LOCATE SUCH A SERVICE FACILITY AT A LOCATION WHERE THE
MAXIMUM DISTANCE FROM NEW EMERGENCY FACILITY TO ANY EXISTING USER FACILITIES IS MINIMIZED
• HERE THE CRITERIA ARE THAT THE FARTHEST CUSTOMER HAS TO WALK THE MINIMUM DISTANCE TO
AVAIL THE FACILITY. THAT IS WHY SUCH PROBLEMS ARE CALLED MINIMAX LOCATION PROBLEM.

19. CONTD.
• WE NEED THE LOCATION COORDINATES OF EXISTING FACILITIES OR USER FACILITIES. IN SUCH CASES
DETERMINING MAXIMUM DELAY IS MORE IMPORTANT TO EVALUATE THE EFFECTIVENESS OF SERVICE
DELIVERY THAN AVERAGE OR TOTAL DELAY IN PROVIDING SERVICE
• . CONSIDER THERE ARE N EXISTING FACILITIES WITH LOCATION COORDINATES (X1, Y1), (X2, Y2), (X3, Y3),…
(XN, YN) IN X – Y PLANE. WE WANT TO LOCATE NEW FACILITY AT (XR, YR) SUCH THAT THE MAXIMUM
DISTANCE FROM THE NEW FACILITY TO ANY OF THE EXISTING FACILITIES IS MINIMIZED.
• SO, WE WANT TO FIND THE OPTIMAL LOCATION R WITH (XR, YR) COORDINATES.

20. OBJECTIVE FUNCTION
• THE OBJECTIVE FUNCTION FOR MINIMAX LOCATION PROBLEM CAN BE WRITTEN AS

21. THE CENTRE OF GRAVITY MODEL
• THE CENTRE OF GRAVITY METHOD IS ALSO SIMPLE APPROACH. THE COORDINATES OF THE NEW
PLANT(X,Y) ACCORDING TO THIS METHOD ARE GIVEN BY:
x - coordinate =
∑dixli
∑li
i
i
∑diyli
∑li
i
i
y - coordinate =
where dix = x-coordinate of location i
diy = y-coordinate of location i
li = Loads to be transported between the
existing facilities and the new plant.

22. SERVICE FACILITY ON A LINE OR A PLANE
LOCATING FACILITY ON A LINE
• THE TARGET GROUP I.E. GROUP OF CUSTOMERS IS CONCENTRATED THROUGHOUT A LINE WITH DIFFERENT
CUSTOMER DENSITY.
• THE PROBLEM IS SIMILAR TO A SITUATION WHERE A GROCERY RETAILER WANTS TO OPEN A FACILITY ON A
LONG STREET WHERE MANY RESIDENTS STAY.
• THE RETAILER WANTS TO MINIMIZE THE AVERAGE WALK BY THE CUSTOMERS FROM ANYWHERE IN THE
STREET.
• THE RESIDENTIAL AREA HAS ALL KIND OF HOME FACILITIES (MULTI-STORIED TO INDIVIDUAL HOUSES)
WHICH LEADS TO DIFFERENT CUSTOMER DENSITY THROUGHOUT THE STREET

23. • CONSIDER THE FOLLOWING NOTATION TO LOCATE SINGLE FACILITY ON A LINE
• R: SITE OF THE FACILITY OR POSSIBLE LOCATION WHERE A SMALL RETAILER CAN OPEN A SMALL OUTLET.
• XI : LOCATION OF THE ITH DEMAND POINT FROM THE ORIGIN (ANY ONE END OF THE STREET CAN CONSIDER AS ORIGIN).
• WI: RELATIVE WEIGHT OF DEMAND ATTACHED TO THE ITH LOCATION BASED ON CUSTOMER DENSITY.
• THE OBJECTIVE FUNCTION Z IS TO MINIMIZE THE DISTANCE TRAVELLED BY THE CUSTOMERS EITHER SIDE OF THE
STREET.
• CONSIDER THE WEST END OF THE STREET TO BE ORIGIN AS SHOWN IN FIGURE 6.17. WE WANT TO LOCATE R ON XI
WHERE IT RANGES FROM 0 TO N.

24. CUSTOMER DENSITY ON A STREET

25. • THE OPTIMUM Z WILL BE ACHIEVED IF R IS LOCATED AT THE MEDIAN WITH RESPECT TO THE DENSITY
DISTRIBUTION OF CUSTOMERS OR RESIDENTS RESIDING ON A STREET BETWEEN N=9 AND N=10

26. • THE OPTIMUM Z WILL BE ACHIEVED IF R IS LOCATED AT THE MEDIAN WITH RESPECT TO THE DENSITY
DISTRIBUTION OF CUSTOMERS OR RESIDENTS RESIDING ON A STREET BETWEEN N=9 AND N=10

27. LOCATING A FACILITY ON A PLANE WITH
RECTILINEAR METRIC
• A FACILITY CAN BE LOCATED ON A PLANE IN A SIMILAR FASHION AS WE DID ON LINE WITH ONLY DIFFERENCE IS THE
CONSIDERATION OF X AND Y COORDINATES. THE PROBLEM ON A PLANE CAN BE DESCRIBED AS

28. EXAMPLE: LOCATING MED HOSPITAL IN A CITY
• CONSIDER A PROBLEM OF LOCATING A HOSPITAL IN A RECTILINEAR CITY WITH THE EXISTING DEMAND
COORDINATES AND CORRESPONDING DENSITY WEIGHTS AS GIVEN IN TABLE 6.5. THE CITY IS DIVIDED INTO
SMALL 5 REGIONS WHERE DEMAND IS CONCENTRATED AND CONSIDERED TO BE AT ONE POINT IN EACH
REGION. THE REGIONS CAN BE PLOTTED ON X-Y COORDINATE

29. WHERE TO LOCATE R?

31. • TO MINIMIZE THE TOTAL DISTANCE TRAVELLED BY THE CUSTOMERS IN A METROPOLITAN REGION
(MOSTLY SEEN IN URBAN AREAS), CROSS MEDIAN APPROACH IS USED.

32. FIND THE X COORDINATE MEDIAN FOR XR TO
LOCATE R
• STEP 1:- ADD THE VALUES OF WI IN THE X-DIRECTION WHILE GOING FROM WEST TO EAST AND EAST TO
WEST.
• STEP 2:- LIST DOWN THE DEMAND REGION AS THEY APPEAR IN ASCENDING ORDER (DESCENDING ORDER)
FROM WEST TO EAST (EAST TO WEST).
• STEP 3:- THE WEIGHTS ATTACHED TO EACH POINT IS SUMMED IN ASCENDING ORDER (DESCENDING
ORDER) FOR WEST TO EAST (EAST TO WEST) UNTIL THE MEDIAN VALUE I.E. 1900 IS REACHED OR
EXCEEDED.

37. LOCATING A SINGLE FACILITY ON A PLANE
WITH EUCLIDEAN DISTANCE METRIC
• IN MOST REAL CASES, THE DISTANCE BETWEEN FACILITIES IS MEASURED IN EUCLIDEAN METRIC. THE
SAME OBJECTIVE OF MINIMIZING THE TRAVEL DISTANCE BY THE DEMAND POINTS FOLLOWING EUCLIDEAN
METRIC CAN BE WRITTEN AS

40. HOW TO START WITH XR AND YR?
• ONE INTUITIVE WAY TO INITIALIZE THE PROBLEM IS TO USE CENTER OF GRAVITY METHOD. THE CENTER OF
GRAVITY IS THE AVERAGE LOCATION OF THE WEIGHT OF AN OBJECT. WE CAN USE THE AVERAGE WEIGHTED
LOCATION OF NEW FACILITY AS A STARTING SOLUTION TO FIND THE EXACT LOCATION OF R.

45. QUANTITATIVE MODELS FOR MULTIPLE SERVICE FACILITIES
LOCATION MULTIPLE SERVICE FACILITIES: LOCATION SET COVERING PROBLEM
• SO FAR WE HAVE SEEN THE CRITERIA ADOPTED FOR LOCATION OF SINGLE FACILITY IS EITHER MAXIMIZE PROFIT OR MINIMIZE
WEIGHTED DISTANCE.
• SIMILAR TO THE MINIMAX LOCATION PROBLEM, MOST OF THE PUBLIC SERVICES ARE INTERESTED IN LOCATING MINIMUM
NUMBER OF FACILITIES SUCH THAT THE FACILITIES COVER OR SERVE ALL THE DEMAND POINTS WITH MAXIMAL SERVICE
DISTANCE.
• MAXIMAL SERVICE DISTANCE IS THE DISTANCE THAT MOST DISTANT CUSTOMER WOULD HAVE TO TRAVEL TO REACH THE
FACILITY. SUCH PROBLEM OF LOCATING MULTIPLE FACILITIES IS ALSO KNOWN AS LOCATION SET COVERING PROBLEM.
EXAMPLE:
• LOCATING MINIMUM NUMBER OF FOOD GRAIN SUPPLY OUTLETS UNDER PUBLIC DISTRIBUTION SYSTEM TO SUPPLY FOOD
GRAINS TO VARIOUS REGIONS
• LOCATING MINIMUM NUMBER OF HEALTH CLINICS TO VARIOUS SITES IN A CITY.

46. EXAMPLE: PROBLEM STATEMENT
• A CITY XYZ WANTS LOCATE HEALTH CLINICS IN 10 CUSTOMER REGIONS PRESENTED IN A NETWORK IN
FIGURE 6.24. THE NODES OF THE NETWORK PRESENT THE DEMAND POINTS OR CUSTOMER REGIONS AND
THE ARCS CONNECTING NODES REPRESENT THE DISTANCE BETWEEN THE NODES IN KILOMETERS. XYZ
WANTS TO LOCATE MINIMUM NUMBER OF HEALTH CLINICS WITH MAXIMAL SERVICE DISTANCE OF 15KM.
EACH DEMAND POINT CAN SERVE AS A POTENTIAL LOCATION OF HEALTH CLINIC SERVICE.
FIGURE : A NETWORK FOR POTENTIAL LOCATIONS TO LOCATEHEALTH CLINIC BY XYZ

47. MAXIMAL SERVICE DISTANCE IS 15 KM. THERE ARE I=10 DEMAND POINTS AND WE WANT TO LOCATE J
FACILITIES.
WE WILL FIRST FIND THE SET OF ALL DEMAND POINTS WHICH CAN BE SERVED BY LOCATING FACILITY AT
EACH ITH POINT

48. We know that all i points can be potential sites to locate health clinic.
Find the subsets of other potential locations to reduce the problem size and place them in parentheses as
shown in Table

50. • SELECT THE SITES WHICH ARE COMMON TO TWO OR MORE OF THE SUBSETS FOR EXAMPLE:4,5,8,9 AND 10.
WE CAN SEE FROM THE NETWORK THAT 3 SITES AT THE NODES 2, 4, AND 9 CAN SERVE ALL THE OTHER
LOCATIONS
• 2 - 1, 2, 4
• 4 - 2, 3, 4, 5, 6, 8
• 9 - 7, 8, 9, 10
• THE ABOVE PROBLEM CAN BE OPTIMALLY SOLVE BY USING ZERO-ONE PROGRAMMING MODEL AS
DESCRIBED BELOW

51. ANY QUERIES?????