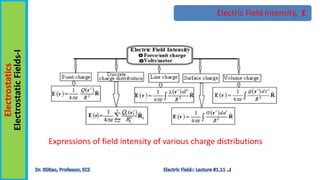
This document summarizes a lecture on electrostatics and electric field intensity. It defines electric field intensity as the force exerted by an electrostatic field on a unit positive charge placed at that point. It then provides the equations for calculating electric field intensity from discrete point charges and various continuous charge distributions such as line charges, surface charges, and volume charges. The document expresses that the electric field intensity is found by integrating the contribution of small charge elements over the whole charge distribution. It concludes by stating the expressions for calculating electric field intensity from different charge distributions.

1. Series: EMF Theory
Lecture: #1.11
Dr R S Rao
Professor, ECE
ELECTROSTATICS
Passionate
Teaching
Joyful
Learning
Electric field intensity, definition, field intensity for discrete charge distributions,
line charge distribution, surface charge distribution and volume charge distribution.

2. Electric Field Intensity, E
•Electrostatic field intensity at a point in the field can be
defined as
'the force exerted by the field on a unit positive charge
placed at that point'.
•It is indicated by English capital letter, E and its units are V/m.
•Using Coulomb's law, the intensity of the field due to a point
charge can be found.
2 2
1
1 1
ˆ ˆ
4 4
q
Qq Q
R R
 

  
F R E = F R
Electrostatics
Electrostatic
Fields-I

3. Electric Field Intensity, E
Field obeys superposition principle and expression for a single
point charge can be extended to other distributions.
In case of group of point charges,
1 2
1 2
1 2
2 2 2
1 2
2
1
......
1 ˆ ˆ ˆ
.....
4
1 ˆ
4
n
n
n
n
n
k
k
k k
Q
Q Q
R R R
Q
R

 
  
 
   
 
 
 
E = E E E
R R R
R
Electrostatics
Electrostatic
Fields-I

4. Continuous charge distributions.(a) line, (b) surface and(c) volume types.
Charge Distributions
•Charges are available in two types of distributions, discrete
and continuous.
•In continuous, three types are there, line, surface and volume.
Electrostatics
Electrostatic
Fields-I
4

5. 2 2
1 1 λ
ˆ ˆ
4 4
dQ dl
R R
 
 
E = R = R
2 2
1 1 σ
ˆ ˆ
4 4
dQ da
R R
 
 
E = R = R
2 2
1 1 ρ
ˆ ˆ
4 4
dQ d
R R

 
 
E = R = R
2 2 2
1 1 1
ˆ ˆ ˆ
4 4 4
Q dQ dQ
d d
R R R
  
   
E = R E = R E = E = R
In case of line charge, dQ = λdl , in case of surface charge, dQ = σda and
in case of volume charge, dQ = ρdτ
←Line charge
← Surface charge
← Volume charge
For continuous distributions,
Electric Field Intensity, E
Electrostatics
Electrostatic
Fields-I
5

6. Expressions of field intensity of various charge distributions
Electric Field Intensity, E
Electrostatics
Electrostatic
Fields-I

7. ENOUGH
FOR
TODAY
ENOUGH
FOR
TODAY
ENOUGH
FOR
TODAY
ENOUGH
FOR
TODAY
ENOUGH
FOR
TODAY
7