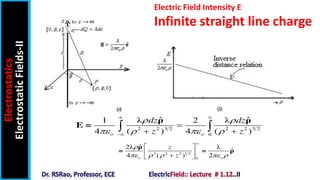
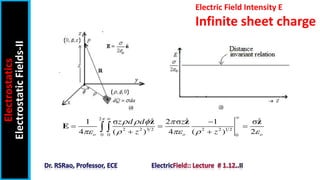
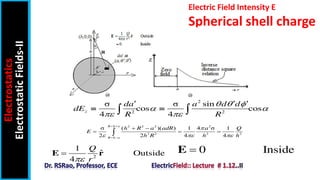
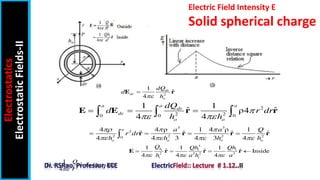
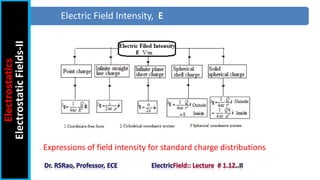
The document discusses electric field intensity due to various charge distributions. It covers infinite straight line charges, infinite plane sheet charges, spherical shell charges, and solid spherical charges. For each charge distribution, it describes the appropriate coordinate system, locating the charge distribution over the system, and selecting the correct field formula to calculate the electric field intensity. Expressions for the electric field intensity both inside and outside the charge distribution are provided. The goal is to derive expressions for the electric field intensity for standard charge distributions in electrostatics.

1. Series: EMF Theory
Lecture: #1.12
Dr R S Rao
Professor, ECE
ELECTROSTATICS
Passionate
Teaching
Joyful
Learning
Electric field intensity due to infinite straight line charge, infinite plane sheet charge,
spherical shell charge and solid spherical charge.

2. Electric Field Intensity E
Solution procedure
Electrostatics
Electrostatic
Fields-II
2
• Infinite straight line charge
• Infinite plane sheet charge
• Hollow spherical shell-inside and outside
• Solid spherical charge-inside and outside
Four types of charge distributions considered:

3. Electric Field Intensity E
Solution procedure
Electrostatics
Electrostatic
Fields-II
3
• Selecting appropriate coordinate system: If the source exhibits cylindrical
symmetry, like infinite straight line, cylindrical coordinate system is best
suited. The spherical coordinate system requires to be used when the
source exhibits spherical symmetry.
• Locating the source over the coordinate system: When it is placed
properly, the solution becomes incredibly simple and easy.
• Selecting appropriate field formula: Depending upon the source
distribution, one of the formulas, available for line charge, surface
charge and volume charges, is to be selected.
The solution procedure involves:

4. Coordinate system→ Cylindrical system
Location→ charge over z-axis with field point over xy-plane
Electric Field Intensity E
Infinite straight line charge
Formula→ 2
1 λ ˆ
4
dl
R
 
E = R
2 2 2
2 2 1 2
ˆ ˆ
( )
ˆ
, ( ),
( )
z
dl dz R z
z




   

ρ z
R
Charge at +z gives a –z field component at P which is cancelled by the
+z component given by the charge at –z, leaving behind only radial
components.
Electrostatics
Electrostatic
Fields-II
4

5. 2 2 3 2 2 2 3 2
0
ˆ ˆ
1 λ 2 λ
4 ( ) 4 ( )
o o
dz dz
z z
 
   
 


 
 
ρ ρ
E =
2 2 2 1 2
0
ˆ
2λ λ
ˆ
4 ( ) 2
o o
z
z

    

 
 

 
ρ
= = ρ
Electric Field Intensity E
Infinite straight line charge
Electrostatics
Electrostatic
Fields-II

6. Formula→
Electric Field Intensity E
Infinite sheet charge
2
1 σ ˆ
4
da
R
 
E = R
Two charges diametrically opposite give normal to z field components at
P in opposite directions, cancelling each other, leaving behind on z
components.
2 2 2
2 2 1 2
ˆ
ˆ
( )
ˆ
, ( ),
( )
z
da d d R z
z

   


   

z
R

Electrostatics
Electrostatic
Fields-II
6
Coordinate system→ Cylindrical system.
Location→ charge over xy-plane with field point over z-axis.

7. 2
2 2 3 2 2 2 1 2
0 0 0
ˆ ˆ ˆ
1 σ 2 σ 1 σ
4 ( ) 4 ( ) 2
o o o
z d d z
z z

   
    



  
 
 
z z z
E
Electric Field Intensity E
Infinite sheet charge
Electrostatics
Electrostatic
Fields-II

8. Coordinate system→ Spherical system.
Location→ Center of charge over the origin.
Formula→
Electric Field Intensity E
Spherical shell charge
2
1 σ ˆ
4
da
R
 
E = R
2 2 2 2
sin , 2 cos
da a d d R h a ha
   
   
  
=
Electrostatics
Electrostatic
Fields-II
8

9. 2
2 2
σ σ sin
cos cos
4 4
z
da a d d
dE
R R
  
 
 
  
 
= =
2 2 2 2
2 2 2 2
σ ( )( ) 1 4 σ 1
2 2 4 4
R h a
R h a
h R a adR a Q
E
h R h h

  
 
 
 
  

2
1
ˆ Outside
4
Q
r


E r 0 Inside

E
Electric Field Intensity E
Spherical shell charge
Electrostatics
Electrostatic
Fields-II

10. Electric Field Intensity E
Solid spherical charge
Electrostatics
Electrostatic
Fields-II
10
Coordinate system→ Spherical system
Location→ Center of sphere right over the origin
The given solid sphere is divided into thin shells of thickness dr.
The field due to each shell is available and fields due to all the
shells are then added by integration to get field due to the entire
solid sphere.

11. 2
2 2
0 0 0
1 1
ˆ ˆ
ρ4
4 4
a a a
dr
dr
o o
dQ
d r dr
h h

 
  
  
E E r r
2
1
ˆ
4
dr
dr
o
dQ
d
h


E r
3 3
2
2 2 2 2
0
4 4 ρ 1 4 ρ 1
ˆ ˆ ˆ ˆ
4 4 3 4 3 4
a
o o o o
a a Q
r dr
h h h h
  
   
   
 r r r r
2
1
ˆ Outside
4
Q
r

 
E r
3
2 3 2 3
1 1 1
ˆ ˆ ˆ Inside
4 4 4
i
h i i
i i
Q Qh Qh
h a h a
  
   
E r r r
Electric Field Intensity E
Solid spherical charge
Electrostatics
Electrostatic
Fields-II

12. Expressions of field intensity for standard charge distributions
Electric Field Intensity, E
Electrostatics
Electrostatic
Fields-II

13. ENOUGH
FOR
TODAY
ENOUGH
FOR
TODAY
ENOUGH
FOR
TODAY
ENOUGH
FOR
TODAY
ENOUGH
FOR
TODAY
13