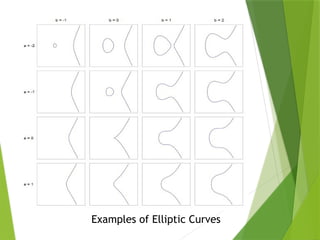
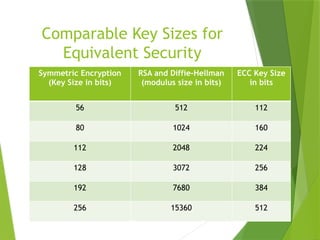
The document discusses elliptic curve cryptography (ECC), highlighting the mathematical basis of elliptic curves and their properties. It emphasizes ECC's advantages, such as shorter key lengths and reduced computational complexity, making it efficient and secure for various applications. Additionally, it outlines the ECC algorithm for key generation, encryption, and decryption, while mentioning the pros and cons of ECC compared to traditional cryptographic methods.

1. ELLIPTIC CURVE
CRYPTOGRAPHY
By
Manvi Molpariya
Sameena Khan

2. Introduction
 What are Elliptic Curves?
 Curve with standard form y2
= x3
+ ax + b
a, b ϵ ℝ
 Characteristics of Elliptic Curve
 Forms an abelian group
 Symmetric about the x-axis
 Point at Infinity acting as the identity element

3. Examples of Elliptic Curves

4. Why Elliptic Curve
Cryptography?
 Shorter Key Length
 Lesser Computational Complexity
 Low Power Requirement
 More Secure

5. Key concept of elliptic curve
crytography
 Elliptic Curve: An elliptic curve is represented by an equation of the
form:
y2=x3+ax+b
 Group Law: Points on the elliptic curve form an algebraic structure
called a group, where the group operation (usually referred to as
"addition") is defined geometrically.
a) Point Addition: If you have two points P and Q on the curve, the sum
R=P+Q is computed using the geometry of the curve.
b) Point Doubling: If P =Q, the result is called doubling the point, 2P,
calculated similarly.
 Discrete Logarithm Problem: The security of ECC is based on the
elliptic curve discrete logarithm problem (ECDLP). Given points P and
Q on the curve, where Q=kP for some integer k, it's computationally
infeasible to determine k, even if P and Q are known.

6. Comparable Key Sizes for
Equivalent Security
Symmetric Encryption
(Key Size in bits)
RSA and Diffie-Hellman
(modulus size in bits)
ECC Key Size
in bits
56 512 112
80 1024 160
112 2048 224
128 3072 256
192 7680 384
256 15360 512

7. ECC Algorithm
1. Key Generation
 Select a curve and a base point (G): An elliptic curve is in the form:
= + ax +b(mod p) where a,b and p(a prime number) Elliptic curve cryptography
work on finite field means all calculation done within finite set of number which
is done using modular arithmetic
 Private key:
 A random integer is selected as the private key, where 1<<n (n is the order
of the elliptic curve)
 Public key:
 The corresponding public key PA​is calculated as:
=×G
where G is the base point and is the private key. The public key is a point on
the elliptic curve.

8. ECC Algorithm
2. Encryption Process:
 Generate a shared secret code: The sender chooses random integer k which will
be kept secret
 Calculate the shared point: The sender compute P = k x G where G is the base
point
 Encrypt the message: The message M is represented as the point on eliptic curve
 The cipher text will contain 2 parts:
1. C1​
=k×G
2. C2=M+k×
 Where is the recipient public key and k is random integer

9. ECC Algorithm
 Decryption:
To decrypt the receiver uses their private key
1. decrypt the first part: Multiply C1 by private key x C1
2. Subtract this result from C2 to recover message M
M= C2 –( x C1) Then we will get the point of message

10. Numerical
Parameter
 Elliptic Curve Equation:
This defines the elliptic curve over a finite field.
 Base Point G: The base point on the curve is:
G=(3,10)
 Prime p: we use p=23
 Private Key dA: The private key dA​is 6
 Public Key PA​
: The public key is computed using scalar multiplication: PA=dA X G

11. Numerical

12. Numerical

13. Numerical

14. Pros and Cons
 Pros
 Shorter Key Length
 Same level of security as RSA achieved at a much shorter key
length
 Better Security
 Secure because of the ECDLP
 Higher security per key-bit than RSA
 Higher Performance
 Shorter key-length ensures lesser power requirement – suitable
in wireless sensor applications and low power devices
 More computation per bit but overall lesser computational
expense or complexity due to lesser number of key bits

15. Pros and Cons
 Cons
 Relatively newer field
 Idea prevails that all the aspects of the topic may not have
been explored yet – possibly unknown vulnerabilities
 Doesn’t have widespread usage
 Not perfect
 Attacks still exist that can solve ECC (112 bit key length has
been publicly broken)
 Well known attacks are the Pollard’s Rho attack
(complexity O(√n) ), Pohlig’s attack, Baby Step,Giant Step
etc