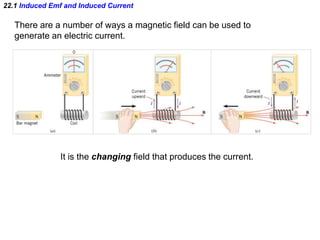
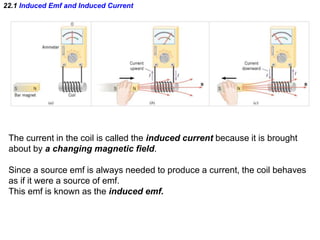
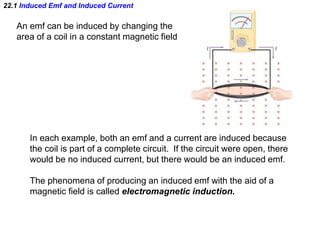
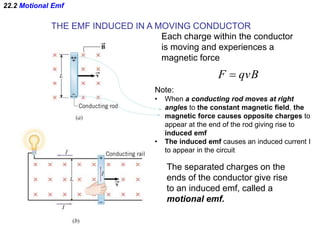
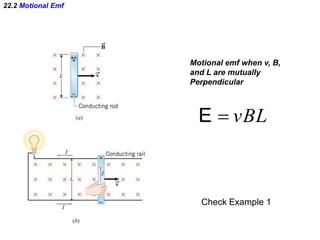
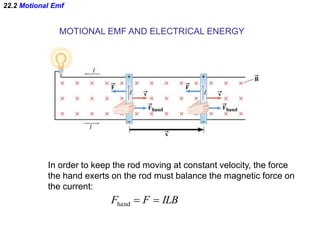
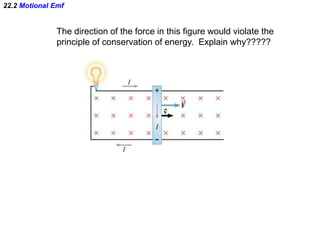
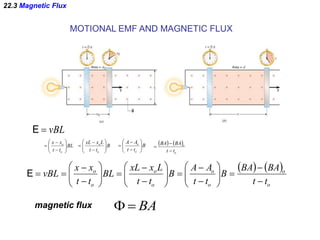
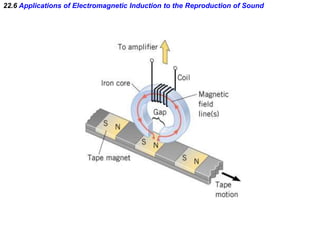
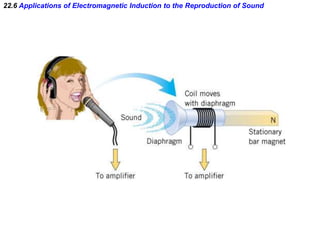
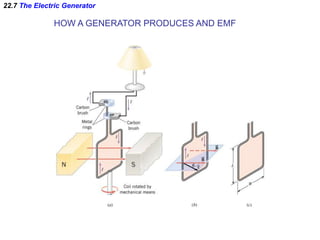
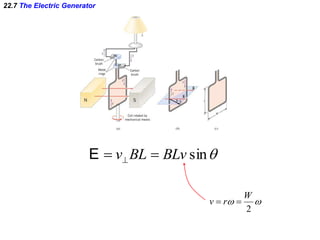
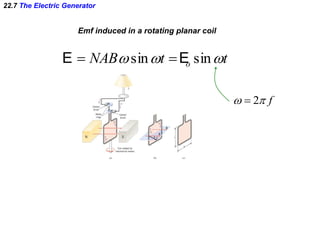
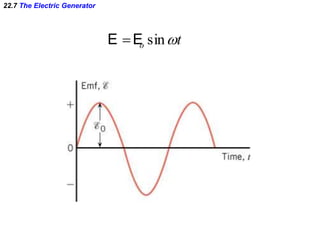
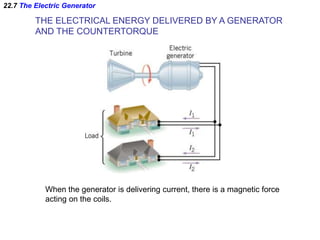
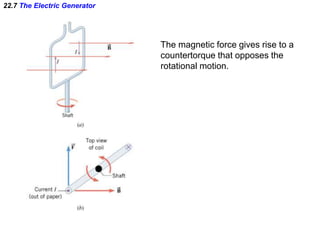
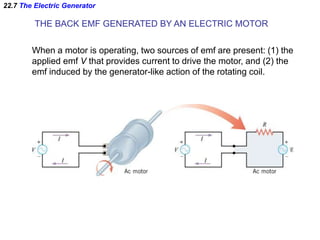
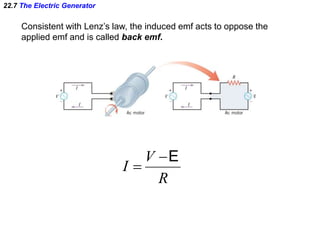
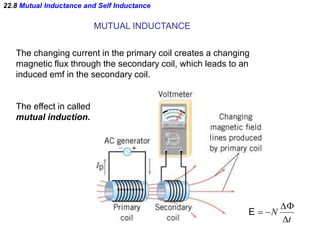
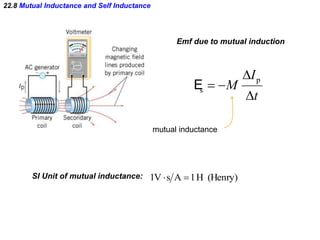
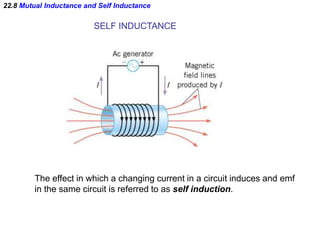
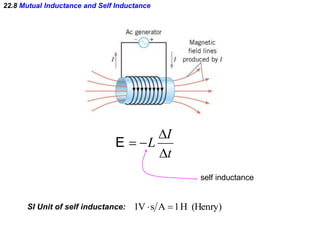
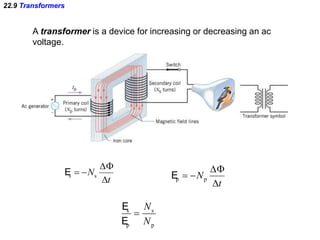
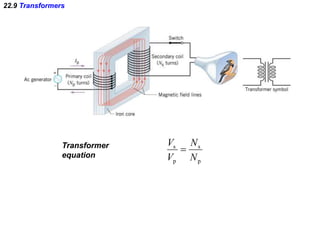
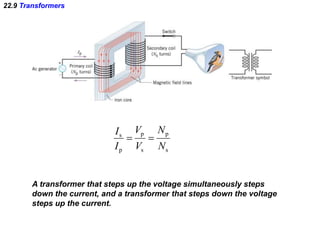
- Electromagnetic induction occurs when a changing magnetic field induces an electromotive force (emf) in a conductor. This induced emf can drive an electric current.
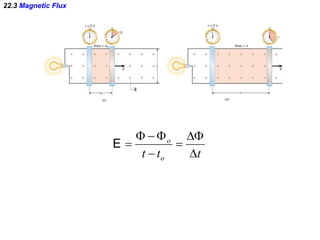
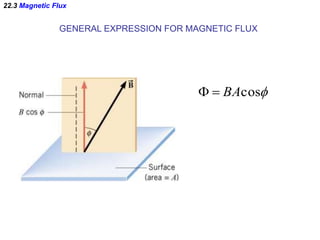
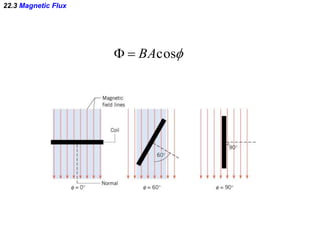
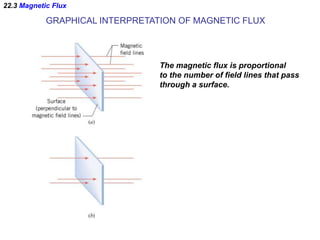
- Faraday's law of induction states that the induced emf in a coil is proportional to the rate of change of the magnetic flux through the coil. A changing magnetic field is necessary to induce an emf and current.
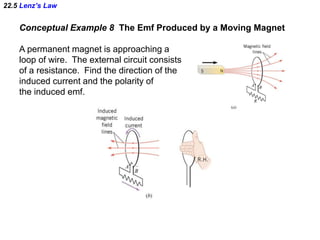
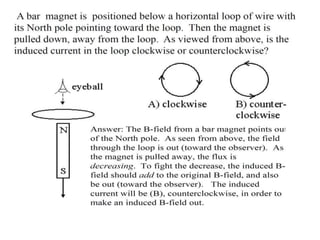
- Lenz's law describes the direction of the induced current: the current will flow in the direction that opposes the change producing it. This ensures the law of conservation of energy is obeyed.
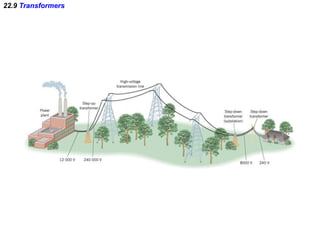
- Transformers take advantage of electromagnetic induction to change the voltage of an alternating current (AC) while transmitting power efficiently over