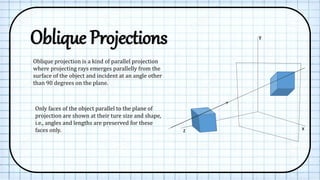
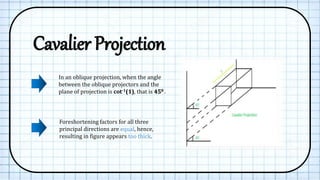
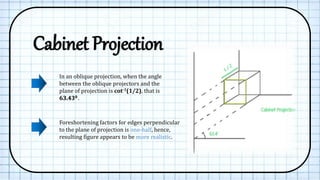
The document discusses oblique projections in computer graphics, detailing how they differ from other projection types like orthographic and perspective projections. It explains specific cases such as cavalier and cabinet projections, including the angles and foreshortening effects associated with each. Additionally, the transformation matrices for oblique projections are described, highlighting their application in preserving shapes and sizes of certain object faces.

1. COMPUTER GRAPHICS
Oblique Projections
Shalvi Dhoundiyal
(B.Sc. Hons. Computer Science)
(III-year)

2. Plane geometric projections
Parallel Perspective
Orthographic
Three-point
Two-point
Single-point
Axonometric Oblique
Cavalier Cabinet
Isometric
Dimetric
Trimetric

3. Oblique Projections
Oblique projection is a kind of parallel projection
where projecting rays emerges parallelly from the
surface of the object and incident at an angle other
than 90 degrees on the plane.
Only faces of the object parallel to the plane of
projection are shown at their ture size and shape,
i.e., angles and lengths are preserved for these
faces only.
y
x
z

4. Special Cases of Oblique projection
When the angle between the oblique
projectors and the plane of projection is :
cot-1(1) = 450
When the angle between the oblique
projectors and the plane of projection is :
cot-1(1/2) = 63.430
( Depending upon the angle between projectors and plane of projection. )
Cavalier Projection Cabinet Projection

5. Cavalier Projection
In an oblique projection, when the angle
between the oblique projectors and the
plane of projection is cot-1(1), that is 450 .
Foreshortening factors for all three
principal directions are equal, hence,
resulting in figure appears too thick.

6. Cabinet Projection
Foreshortening factors for edges perpendicular
to the plane of projection is one-half, hence,
resulting figure appears to be more realistic.
In an oblique projection, when the angle
between the oblique projectors and the
plane of projection is cot-1(1/2), that is
63.430 .

7. Transformation for an Oblique Projection
Consider a unit vector [ 0 0 1 ] along the z-axis.
Here, P1O and PP2 are typical oblique projectors and z = 0 is the plane of projection.
β = angle between projectors and plane of projection.
Translating point P by -a in x-direction and -b in y-direction to point P1 at [ -a -b 1 ].
So,
Transformation Matrix
( 2-Dimension )
1 0 0
0 1 0
-a -b 1
[ T’ ] =

8. <
<
y
x
z
P [ 0 0 1 ]
P2
O
P1
a
-a
b
-b
α
β
β
Direction of the Oblique Projection Matrix
f

9. In 3-Dimensions, this 2-Dimensional transition is equivalent to shearing of the vector PO in the x
and y direction.
So,
Transformation Matrix
( 3-Dimension )
[ T’’ ] =
1 0 0 0
0 1 0 0
-a -b 1 0
0 0 0 1
Here,
Projection onto the z = 0 plane yields,
[ T ] =
1 0 0 0
0 1 0 0
-a -b 0 0
0 0 0 1

10. a = f cos α
b = f sin α
f is the projected length of the z-axis unit vector.
α is the angle between the horizontal and the projected z-axis.
the angle between projectors and plane of projection,
β = cot-1 ( f )
So,
Thus,
transformation for an Oblique projection is :
[ T ] =
1 0 0 0
0 1 0 0
- f cos α - f sin α 0 0
0 0 0 1
We have,

11. if f = 0,
=> β = 900,
this is an Orthographic Projection.
Now,
if f = 1,
=> β = cot -1 (1) = 450,
the edges perpendicular to the projection plane are not foreshortened.
This is the condition for a Cavalier Projection.
if f = 1/2,
=> β = cot -1 (1/2) = 63.4350,
the edges perpendicular to the projection plane are foreshortened by one-half.
This is the condition for a Cabinet Projection.

12. Most suited for...
Illustrating circular objects or otherwise curved faces.
Why?
To prevents unwanted distortion,
as it happens in most of the parallel projections, when one dimension is significantly larger
than others, unless itself is parallel to plane of projection.

13. Thank You!