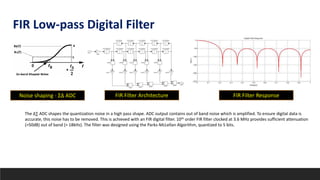
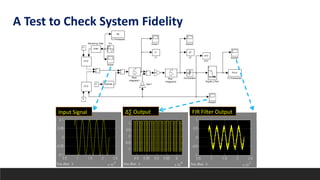
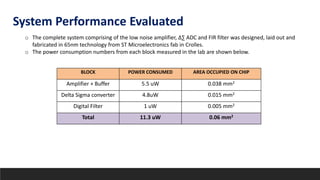
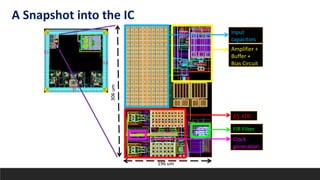
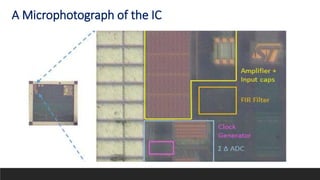
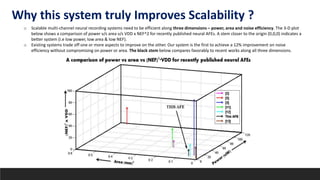
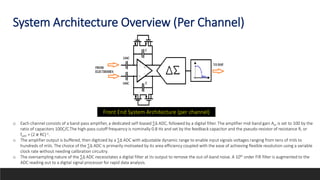
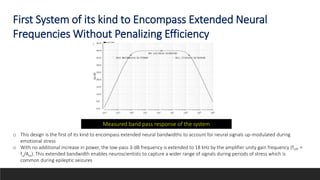
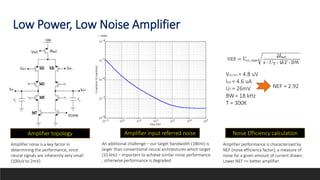
This document summarizes a research paper on developing an efficient multi-channel neural recording system. The system aims to integrate neural recording devices, rapid data analysis to detect seizure onsets, and signal injection to mitigate seizures into an implantable system. Key challenges addressed include scalability, safety standards, power limitations, and noise. The proposed system uses a low-power, low-noise amplifier and second-order delta-sigma ADC per channel, along with a digital FIR filter. Testing showed the system achieves 12% better noise efficiency than prior work, addressing scalability challenges across power, area, and noise.

1. An Efficient Multi-channel Neural
Recording System
UCLA NEUROENGINEERING
AUG 2013

2. Disabilities such as autism,
epilepsy & paralysis are closely
linked to the functioning of the
brain and the neural systems
A key neuroscience focus area is
building automated prediction
and mitigation capabilities for
epileptic seizures
Research indicates that seizures
or epileptic fits can be predicted
and mitigated by continuous brain
monitoring and pattern
recognition
Multi-channel neural systems
aim to integrate neural
recording devices, rapid data
analysis to detect seizure
onsets and signal injection to
mitigate seizures into efficient
implantable systems
Motivation

3. Constraints of Building a Neural System
Scalability
To ascertain neural patterns
from the entire brain, a large
surface area of the brain needs
to be probed, resulting in
systems of over 1000 channels
that need to fit into an
implantable system. Scalability
from single to multi-channel is
crucial
FCC Safety Standards
International safety
standards and FCC
regulations stipulate that
the maximum current that
can be injected into the
human brain is 500uA.
The entire system should
operate far below this
safety limit
Power Limitations
Neural recording systems need
to operate at ultra-low power
since high power results in high
heat dissipation. Research
suggests that a heat flux of
80mW/cm2 can cause muscle
necrosis, endangering the
patient
Tiny signals amidst Big noise
Neural signals are very weak and
are easily affected by circuit noise
and environmental noise. It is
crucial to design the neural
system to add minimum noise
while retaining the fidelity of the
brain signals

4. Comparison: Electrode area vs. Size of Skull
Power Breakup of each module in a multi-
channel neural signal acquisition system
Source: Wattanapatich, Fee & Sarpeshkar,
[Massachusetts Institute of Technology]
Source: Chandler, Farshchi & Judy,
[University of California, Los Angeles]
Constraints of Building a Neural System

5. System Architecture Overview (Per Channel)
o Each channel consists of a band-pass amplifier, a dedicated self-biased ∑∆ ADC, followed by a digital filter. The amplifier mid-band gain Am is set to 100 by the
ratio of capacitors 100C/C.The high-pass cutoff frequency is nominally 0.8 Hz and set by the feedback capacitor and the pseudo-resistor of resistance R, or
fHPF = (2 𝜋 RC)-1.
o The amplifier output is buffered, then digitized by a ∑∆ ADC with adjustable dynamic range to enable input signals voltages ranging from tens of mVs to
hundreds of mVs. The choice of the ∑∆ ADC is primarily motivated by its area efficiency coupled with the ease of achieving flexible resolution using a variable
clock rate without needing calibration circuitry.
o The oversampling nature of the ∑∆ ADC necessitates a digital filter at its output to remove the out-of-band noise. A 10th order FIR filter is augmented to the
ADC reading out to a digital signal processor for rapid data analysis.
Front End System Architecture (per channel)

6. First System of its kind to Encompass Extended Neural
Frequencies Without Penalizing Efficiency
o This design is the first of its kind to encompass extended neural bandwidths to account for neural signals up-modulated during
emotional stress
o With no additional increase in power, the low-pass 3-dB frequency is extended to 18 kHz by the amplifier unity gain frequency (fLPF =
fu/Am). This extended bandwidth enables neuroscientists to capture a wider range of signals during periods of stress which is
common during epileptic seizures
Measured band pass response of the system

7. Low Power, Low Noise Amplifier
Amplifier input referred noise
Vni,rms = 4.8 uV
Itot = 4.6 uA
UT = 26mV
BW= 18 kHz
T = 300K
NEF = 2.92
Amplifier noise is a key factor in
determining the performance, since
neural signals are inherently very small
(100uV to 2mV)
An additional challenge – our target bandwidth (18kHz) is
larger than conventional neural architectures which target
(10 kHz) – important to achieve similar noise performance
, otherwise performance is degraded.
Amplifier performance is characterized by
NEF (noise efficiency factor), a measure of
noise for a given amount of current drawn.
Lower NEF => better amplifier.
Amplifier topology Noise Efficiency calculation

8. SNDR = 62.7 dB ~ 10.1 bit ENOB
Low Power, Flexible Resolution ADC
A model of the 2nd order ΣΔ ADC Simulated performance of the ADC
Depending on the input neural signal, the ADC output could
be anywhere from 6-10 bits, thereby demanding a flexible
resolution. Commonly, SAR ADCs are preferred for lower
power. However, flexible resolution SAR ADCs occupy large
area and require calibration circuitry for higher resolution,
making them inefficient on factors other than power
2nd order ∆∑ ADC was chosen instead for our system with the aim to
make power comparable to SARs while also ensuring area
efficiency. Flexible resolution is achieved by simply changing clock
frequency without any additional requirements. The ADC
performance was modeled in MATLAB to aid design

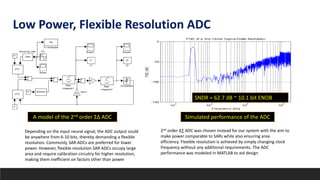
9. Low Power, Flexible Resolution ADC
Circuit implementation of the ΣΔ ADC
Self-biased differential
inverters with auxiliary CMFB
Source: Wang and Theogarajan,
[University of California, Santa Barbara]
The ∆∑ ADC is implemented with the Boser Wooley Architecture
with 1-bit comparator. The integrators in the ADC (shown in red)
are implemented using self biased super inverters which
alleviates the need for bias circuits and being robust across
process corners.
The superinverter as is has weak
common mode feedback. For an ADC
clocked at a few MHz, the common
mode settling of the superinverter is not
fast enough. To alleviate this, a auxillary
switched capacitor CMFB is introduced
to the superinverters. This produced a
fast CMFB settling ensuring that
common mode is stable.

10. The ∆∑ ADC shapes the quantization noise in a high pass shape. ADC output contains out of band noise which is amplified. To ensure digital data is
accurate, this noise has to be removed. This is achieved with an FIR digital filter. 10th order FIR filter clocked at 3.6 MHz provides sufficient attenuation
(>50dB) out of band (> 18kHz). The filter was designed using the Parks-McLellan Algorithm, quantized to 5 bits.
FIR Low-pass Digital Filter
Noise shaping - ΣΔ ADC FIR Filter Architecture FIR Filter Response

11. Input Signal ∆∑ Output FIR Filter Output
A Test to Check System Fidelity

12. o The complete system comprising of the low noise amplifier, ∆∑ ADC and FIR filter was designed, laid out and
fabricated in 65nm technology from ST Microelectronics fab in Crolles.
o The power consumption numbers from each block measured in the lab are shown below.
BLOCK POWER CONSUMED AREA OCCUPIED ON CHIP
Amplifier + Buffer 5.5 uW 0.038 mm2
Delta Sigma converter 4.8uW 0.015 mm2
Digital Filter 1 uW 0.005 mm2
Total 11.3 uW 0.06 mm2
System Performance Evaluated

13. Input
capacitors
Amplifier +
Buffer +
Bias Circuit
∆∑ ADC
FIR Filter
Clock
generation
306um
196 um
A Snapshot into the IC

14. A Microphotograph of the IC

15. o Scalable multi-channel neural recording systems need to be efficient along three dimensions – power, area and noise efficiency. The 3-D plot
below shows a comparison of power v/s area v/s VDD x NEF^2 for recently published neural AFEs. A stem closer to the origin (0,0,0) indicates a
better system (i.e low power, low area & low NEF).
o Existing systems trade off one or more aspects to improve on the other. Our system is the first to achieve a 12% improvement on noise
efficiency without compromising on power or area. The black stem below compares favorably to recent works along all three dimensions.
Why this system truly Improves Scalability ?

16. Collaborators
Ashwath Krishnan
Research Lead
ashwath@ucla.edu
Jack Judy
Faculty Advisor
jack.judy@ucla.edu
Behzad Razavi
Faculty Advisor
razavi@ee.ucla.edu
Shahin Farshchi
Research Advisor
shahin.farshchi@luxcapital.com