This document discusses routing and traffic engineering approaches for IP networks. It covers several topics: metric-based traffic engineering in classical IP networks using hybrid genetic algorithms; routing and re-optimization under partial demand increases; routing and dimensioning in multi-class IP/MPLS networks with per-class over-provisioning; and heuristic approaches for backup capacity provisioning under demand uncertainty. The document outlines computational studies demonstrating the effectiveness of the proposed approaches.

1. Communication Networks
Eueung Mulyana
1
Hamburg – 28.02.2006
Efficient Planning and Offline Routing
Approaches for IP Networks
Eueung Mulyana
Hamburg University of Technology (TUHH)

2. Communication Networks
Eueung Mulyana
2
Motivation
IP Networks:
 The important role of IP technology for the future
communication networks
Current and Future Trends:
 Heterogeneous environment
Routing Control:
 Diverse applications with diverse Quality of Service (QoS)
requirements
 Avoiding congestion, increasing network efficiency, matching
routing policies and preferences
Dynamics of IP networks:
 Traffic variation, uncertainty

3. Communication Networks
Eueung Mulyana
3
Previous Works
„Classical“ IP Networks:
 Traffic engineering: Fortz(2000), Pioro(2001), ...
 Routing and dimensioning: Bley(1998,2002), ...
Multi-Protocol Label Switching (MPLS):
 LSP design: Haßlinger(2002), ...
 Network dimensioning: Arvidsson(2002), ...
Demand Uncertainty:
 Probabilistic assumption: Widjaja(2002), Mitra(2003), ...
 Polyhedral model: Ben-Ameur(2003) ...

4. Communication Networks
Eueung Mulyana
4
Contributions
Classical IP Networks:
 Metric based traffic engineering using hybrid genetic
algorithms
 Traffic engineering for transitional (IGP/MPLS) networks
 Impact of demand increase on network conditions and re-
optimization approaches
IP/MPLS:
 Hybrid routing schemes using metrics and explicit routes
 Routing and dimensioning for multi-class IP/MPLS networks
with per-class over-provisioning requirements
Demand Uncertainty:
 Several simple demand uncertainty models and the
corresponding traffic engineering approaches

5. Communication Networks
Eueung Mulyana
5
Outline
 Overview of network planning, routing in the
Internet and optimization approaches
 Traffic engineering in classical and transitional
IP networks
 Routing and dimensioning of multi-class
IP/MPLS networks
 Routing under demand uncertainty
 Summary and conclusion
Part :
1
2
3
4

6. Communication Networks
Eueung Mulyana
6
Overview of Network Planning
1 2 3 4Part :
Medium-Term Activities
e.g. offline routing management
Short-Term Activities
e.g. (near) real time traffic
and resource management
Long-Term Activities
e.g. network design
Forecast,
Marketing Input
(e.g. new customers)
Network
Traffic Data
Routing Update Various Controls
Traffic DataTopology,
Capacity Change

7. Communication Networks
Eueung Mulyana
7
Routing in the Internet (1)
1 2 3 4Part :
server
www.tuhh.debrowser:
www.tuhh.de
Transport
Network
data streams
Transport
Network
data streams
packets
transport packets
Network
transport packets
packets
Routing

8. Communication Networks
Eueung Mulyana
8
2
1
5
3
4
6
7
8
9
10
server
www.tuhh.de
browser:
www.tuhh.de
Routing in the Internet (2)
1 2 3 4Part :
servers
2
5
servers
users
1
servers
users
servers
users
10
9
servers
users8
servers
users7
servers
users
servers
users
users 3
4
6
servers
users
users
servers

9. Communication Networks
Eueung Mulyana
9
Optimization Approaches (1)
1 2 3 4Part :
 Linear programming
 Stochastic approaches based on simple, greedy, meta-
heuristics or a combination of them
Meta-Heuristics
 Genetic Algorithms, Local Search
Hybridization
Simple
Improving
Heuristic
Search
Algorithm
Solution
Improved Solution
Greedy
Heuristic
Search
Algorithm
Solution
e.g. in terms of a sequence of demands
Objective Value

10. Communication Networks
Eueung Mulyana
10
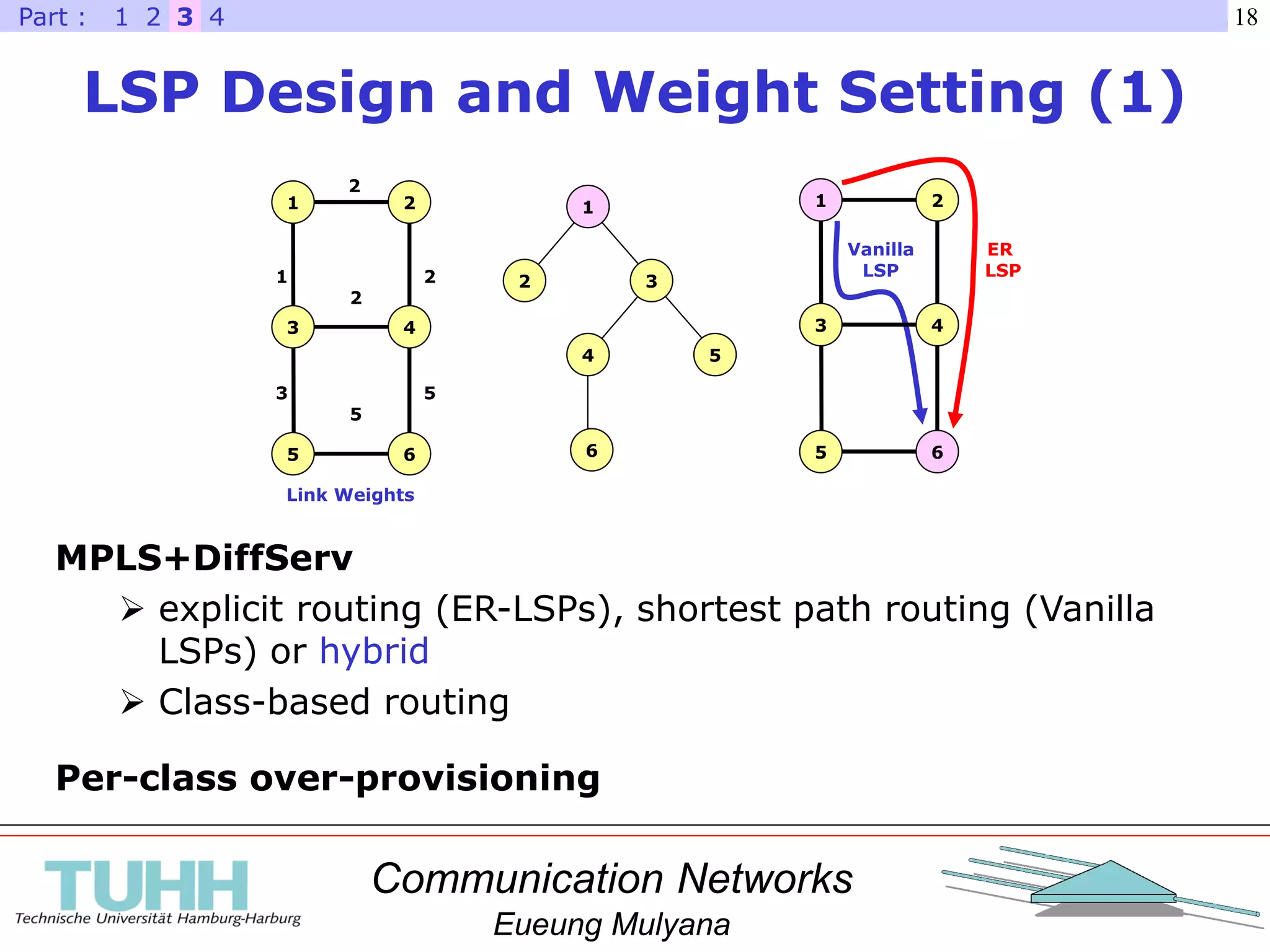
Optimization Approaches (2)
1 2 3 4Part :
Linear programming



n
j
jj xcz
1
i
n
j
jij bxa 
1
Minimize
Subject to: ],1[ mi 
 Can be solved by the branch
and bound or directly by the
simplex algorithm (for cases
without integer constraints)
 Commercial solver CPLEX
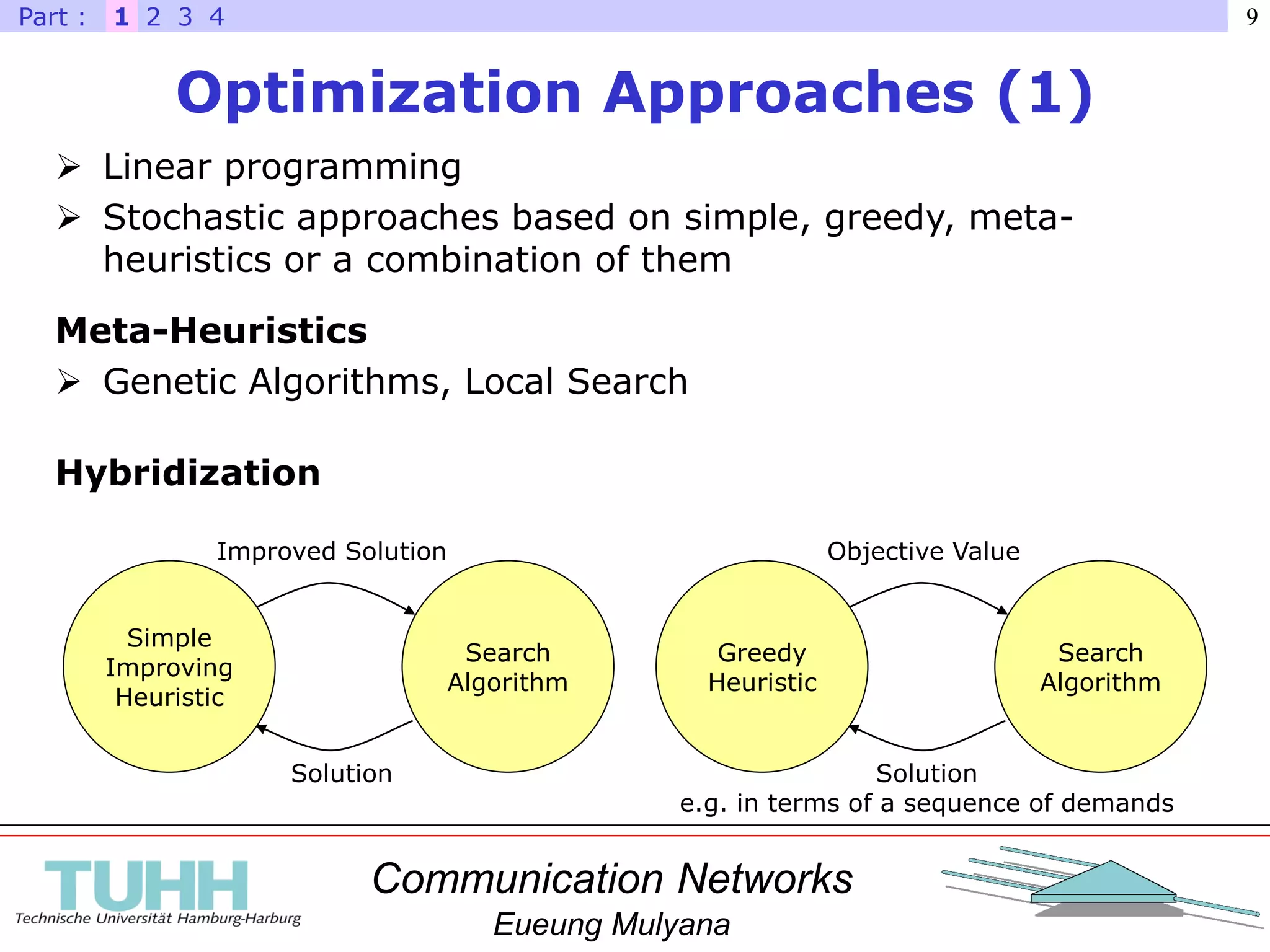
Meta-Heuristics
 Solution representation
 Exploration strategies („move“ or „genetic“ operators)
 Algorithms‘ specific parameters

11. Communication Networks
Eueung Mulyana
11
Local Search (1)
A
B
C
D
E
A B
C
D
1 2 3 4Part :
neighborhood
of A
initial
solution
move
 Plain Local Search (PLS-1)
 Search around temporary
best solutions
 Plain Local Search (PLS-2)
 Search around a constant
solution
neighborhood
of B
neighborhood
of C

12. Communication Networks
Eueung Mulyana
12
Local Search (2)
1 2 3 4Part :
A
B
C
D
E
F
1st
neighborhood
of A
2nd neighborhood
of A
3rd neighborhood
of A
 Variable neighborhood
structure
solution space
neighborhood
of x0
initial
solution x0
best
solution x*
End
temporary
solution x
.
.
.
 Simulated Annealing (SA)
 SA allows moves towards less
performing solutions

13. Communication Networks
Eueung Mulyana
13
Genetic Algorithms
1 2 3 4Part :
solution space
A
B
C
D
E
F
G
H
Initialize population
Exit condition
fulfilled ?
Parents selection
Crossover
Mutation
Remove some bad individuals
Add new individuals
Survivors selection
END
yes
no
individual
Iteration 1
Iteration 3Iteration 2
 Multi-agent (population-based)
 Exploration using crossover and
mutation operators

14. Communication Networks
Eueung Mulyana
14
Routing in IP Networks: IGP
(b)(a)
6
11
1
1
1
1
2
21
2
3
5
5
121
3 4
5 6
2
3 4
5 6
1
2
4
6
5
3
1
2 3
4 5
1
 Driven by link metrics (weights/costs)
 Unique shortest path routing vs. Equal-Cost Multi-Path (ECMP)
ECMP e.g.
[1-2-4-6] 50%
[1-3-4-6] 25%
[1-3-5-6] 25%
Unique shortest path routing:
1 unique path for all node pairs
21 3 4Part :

15. Communication Networks
Eueung Mulyana
15
Metric-Based Traffic Engieering
Utilization Upper bound
Objective Function
}{min max
max,
 ji Aji  ),(
Utilization

uv
vu
jiji ll
,
,,
ji
ji
ji
c
l
,
,
,
 Aji  ),(
21 3 4Part :
Formulation

16. Communication Networks
Eueung Mulyana
16
Transitional IP Networks (IGP/MPLS)
1
2 3
4 5
6
7
8 9
LSP
1
2 3
4 5
6
7
8 9
LSP
1
2 3
4 5
6
7
8 9
LSP
1 3
2 4
5 6
7 8
9
1
1
1
1
1
1
1
2
2
3
2
2
LSP
Basic IGP Shortcut (BIS) IGP Shortcut (IS) Overlay (OV)
21 3 4Part :
}||{min max1
 c  
k
LSP
ji
uv
vu
jiji
k
lll ,
,
,,
Objective Function Load

17. Communication Networks
Eueung Mulyana
17
Network topology
and link capacities
Traffic demand
Partial demand
increase
Re-optimization
Analyze
Policy
not compliant
Weight Changes
Network Upgrade
Set of metric
values
policy compliant
Partial Demand Increase
21 3 4Part :
Mbps]10,5[
,
%2 
vu
f%2
max Mbps]50,5[
,
%2 
vu
f%2
max
Number of traffic-
increase pattern

18. Communication Networks
Eueung Mulyana
18
LSP Design and Weight Setting (1)
Vanilla
LSP
ER
LSP
2
1
2
3
5
2
5
1 2
3 4
5 6
Link Weights
1
2 3
4 5
6
1 2
3 4
5 6
MPLS+DiffServ
 explicit routing (ER-LSPs), shortest path routing (Vanilla
LSPs) or hybrid
 Class-based routing
Per-class over-provisioning
321 4Part :

19. Communication Networks
Eueung Mulyana
19
LSP Design and Weight Setting (2)
 Indirectly solved by iteratively calling a metric-based traffic
engineering (TE) procedure using traffic matrices of different
classes
F  aggregate traffic matrix
Fi  traffic matrix for class i
RT  base routing pattern (obtained via optimization using F )
RTi  routing pattern for class i (obtained via optimization using Fi)
321 4Part :

20. Communication Networks
Eueung Mulyana
20
Computational Study (1)
0.4
OP
1 c
0.4
OP
2 c
 After optimize network(F)
i.e. without ER-LSPs:
)1.1|4.3|3(min 


%44.96max 
321 4Part :

21. Communication Networks
Eueung Mulyana
21
Computational Study (2)
0.4
OP
1 c
0.4
OP
2 c
 After optimize network(F2) :
13 symmetrical ER-LSPs
(premium) and 4
symmetrical ER-LSPs
(assured)
)1.1|01.4|05.4(min 


%68.93max 
321 4Part :

22. Communication Networks
Eueung Mulyana
22
Routing and Link Dimensioning
321 4Part :
1
1
0
1
1
1
1
1 2
3 4
5 6
}2,1{
4
OP
c

 ;20h
100k
1
2
 
e t
ett
ymin
Objective Function
Capacity (with OP)
   







 t
tet
d p i
idpdp
OP
edp
kyxxc
1
1



e ,
Demand Satisfaction
 
p
dp
u 1 d ,
dpddp
uhx 
 pd  ,,
 Per-class routing & per-class
over-provisioning (P1)
 Single-path routing
 Multi-path routing realdp
u
binarydp
u

23. Communication Networks
Eueung Mulyana
23
Backup Capacity
321 4Part :
1 2
3 4 3
21
4
normal
backup
Demand (1,4)
and (3,4)  each
of 20 units
1
3
2
4
40
40
4020
worst case load
on each link
 

 t
tetes
i
idpsidpdps
kyzx 

))(
1
1
se  ,,
 
p
dpsdp
p
dpsdps
uv )1(   sd  ,,
ddsdpsdps
hvz 
 spd  ,,,
  )(( dpsdpdps
OP
d p
edp
zxc 

Demand Rerouting
Capacity
Failure Cases
1
3
2
4
20
20
200
normal case load
on each link

24. Communication Networks
Eueung Mulyana
24
Heuristic Approaches
321 4Part :
Two-step strategy:
 First consider only normal paths (ALG-1)
 Heuristically assign a backup for each normal path

25. Communication Networks
Eueung Mulyana
25
Computational Study
321 4Part :
Problem
(single-path
only)
P1
CPLEX
cost gap(%)
Greedy
(best cost of 100 runs)
P2
P3
165.5 | 268.5
166.5 | 268.5
423.5 | 688
6.18 | 9.93
4.19 | 9.47
3.48 | 3.75
190.5 | 310.5
188.0 | 303.5
453.5 | 755
 The best result from CPLEX is up to 15% (16%) better than
the result from the heuristic
 But, the heuristic (two-step strategy) is faster  minutes vs.
hours

26. Communication Networks
Eueung Mulyana
26
.
.
.
Basic Outbound Model
120-
2
3
4
5
6
100
100
100
100
100
100
1
2
3
4
5
6



}{
out
,
uNv
uvu
ff
)(
, vu
f )( out
u
f
 Specifying a traffic
matrix
 Specifying a vector
of the maximum
outbound traffic
 Allowing traffic
variations
The outbound modelWithout traffic
uncertainty
1 2
20 20 20 20
3 4 5 6
- 20 20 20 20
- 20 20 20
- 20 20
- 20
-
20
20
20
20
20
20
20
20
20
20
20
20
20
20 20
20- 50 5 5 5
- 20 20 20 20
- 20 20 20
- 10 1
- 20
-
20
20
60
20
20
20
20
20
20
2
20
20
20
20 20
20- 20 20 20 20
- 0 99 0 1
- 20 20 20
- 20 20
- 5
-
0
20
20
0
20
20
20
0
20
20
0
20
95
20 20
42 31Part :
u
f out
u
..
. v
Outbound Model
Network

27. Communication Networks
Eueung Mulyana
27
M1
Constraints
Link load
(Upperbound)
M7
M3
M9
uvu
f out
,




}{
out
,
uNv
uvu
ff



u
rv
u
r
vu
ff out,
,
u
r
vu
f out,
,

 



r v
vu
ji
u
r
vu
ji
v
u
r
u
ji
u
r
u
r
fl );max(min
,
,out,
,
,out,, 
Outbound Models
42 31Part :



}{
out
,
uNv
uvu
ff
);max(min
}{
,
,out
,
,
}{
out, 



uNv
vu
ji
uvu
ji
uNv
uu
ji fl 
vu
ji
uNv
uu
ji fl
,
,
}{
out, max 


vu
ji
,
,
Traffic
fraction
of flow (u,v)
on link (i,j)



u
rv
u
r
vu
ff out,
,



r
vu
ji
v
u
r
u
ji
u
r
fl )max(
,
,out,, 

28. Communication Networks
Eueung Mulyana
28
Uncertainty Models : Summary
42 31Part :
u
f out
u
f inu
..
. v
„Hose“ Model
Network
u
f in
u
..
. v
Inbound Model
Network
M2
Model
Model
Notation
outbound
inbound
M1
outbound + max_flow M3
inbound + max_flow M4
hose M5
hose + max_flow M6
M8
outbound + group
inbound + group
M7
outbound + max_flow + group M9
inbound + max_flow + group M10
hose + group M11
hose + max_flow + group M12

29. Communication Networks
Eueung Mulyana
29
Computational Study
 Uncertainty model M1  large number of traffic variations
 A better solution for a certain model is not always better for
the others
Upperbound
(M1)
Traffic Matrix
Utilization
)(, tji
ji ,
t=1
t=100
42 31Part :
Optimization based on M1
MSP  Multiple Shortest Paths
USP  Unique Shortest Path

30. Communication Networks
Eueung Mulyana
30
Partially Uncertain Demands
20-1
2
3
4
)(
, vu
f
1 2
20 20
3 4
- 20 20
- 20
-
20
20
20
20
20 20
60
40
60
40
)( in
u
f
1
2
3
4
60
40
60
40
)( out
u
f
,maxmin()(
,
,
}{
outunc,  

u
vu
ji
uNv
u
ji fl 
 
uv
vu
ji
vu
ji fl
,
,
,
fix, )( 
unc,fix,, )()( jijiji lll 
40
1 2
3 4
40
40
40
60
1 2
3 4
80
60
70
100
1 2
3 4
120
100
110
uncertain
(hose)
fixed
partially
uncertain
)max
,
,
}{
in 

u
uv
ji
uNv
u
f 
42 31Part :

31. Communication Networks
Eueung Mulyana
31
Summary and Conclusion
 Various efficient approaches for offline routing control and
management in diverse IP networks, covering the classical IP
networks as well as MPLS networks with and without service
differentiation
 Some novel mathematical formulations and heuristic
frameworks, taking into account per-class over-provisioning
requirements and different routing strategies
 Our algorithms can find better routing solutions compared to
those given by common routing configurations  improving
network efficiency
 It is also possible to perform minimal routing reconfiguration in
order to keep network performance within an acceptable range

32. Communication Networks
Eueung Mulyana
32
Summary and Conclusion
 Several simple demand uncertainty models whose impacts on
network performance can easily be determined
 The corresponding traffic engineering approach, including for
the case where traffic is partially uncertain
Outlook
 To address planning and traffic management problems in multi-
layer networks e.g. IP over Optical networks
 Mathematical programming approaches, that exploits the
specific structure of the problem  Branch-and-Cut, Branch-
Cut-and-Price

33. Communication Networks
Eueung Mulyana
33
Thank You !