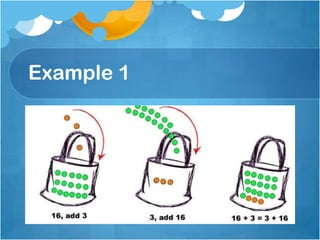
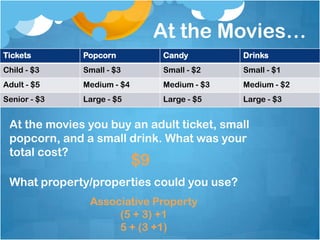
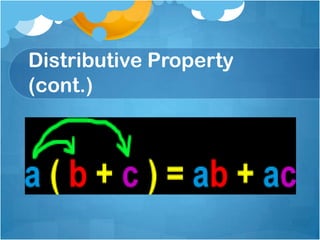
The document provides examples and explanations of various properties of mathematics, including the commutative, associative, identity, and distributive properties as they relate to addition and multiplication. It gives examples of applying these properties to solve equations mentally. It also includes a word problem about distributing baked goods to friends as an example of using the distributive property.

2. Mental Math Warm - Up
1. 18 + (2+7) = 27
2. (18+2) + 7 = 27
3. (95)  4 = 180
4. 9 (54) = 180

3. Commutative Properties of
Addition and Multiplication
The order of the values does
NOT change the sum or
product.

4. Commutative Property of Addition
and Multiplication (Cont.)
Arithmetic Algebra
7+3=3+7 a+b=b+a
24=42 ab=ba

5. Example 1

6. Associative Property of
Addition and Multiplication
The grouping of the values
does NOT change the sum or
product.

7. Associative Property of Addition
and Multiplication (Cont.)
Arithmetic Algebra
(2 + 7) + 3 = 2 + (7 + 3) (a + b) + c = a + (b + c)
(9  4)5 = 9(4  5) (ab)c = a(bc)

8. At the Movies…
Tickets Popcorn Candy Drinks
Child - $3 Small - $3 Small - $2 Small - $1
Adult - $5 Medium - $4 Medium - $3 Medium - $2
Senior - $3 Large - $5 Large - $5 Large - $3
At the movies you buy an adult ticket, small
popcorn, and a small drink. What was your
total cost?
$9
What property/properties could you use?
Associative Property
(5 + 3) +1
5 + (3 +1)

9. Example 2
Use mental math and properties to solve the
following problem: 100  3  2
(100  2)  3 Commutative Property
100  (2  3) Associative Property
= 100  6 Multiply within parentheses
= 600 Solve

10. Identity Property of
Addition
The sum of any number and zero
is the original number.
7+0=7
0+x=x

11. Identity Property of
Multiplication
The product of any number and 1
is the original number.
15  1 = 15
1b=b

12. Example 3
Name each property shown.
34=43 Commutative Property of Multiplication
z1=z Identity Property of Multiplication
 +★=★+ Commutative Property of Addition
5(xy) = (5x)y Associative Property of Multiplication

13. Distributive Property
To multiply a sum or difference, multiply each
number within the parentheses by the number
outside the parentheses.
3(2+6) = 3(2) + 3(6) (2-6)3 = 2(3) – 6(3)
a(b+c) = a(b) + a(c) (b-c)a = ba – ca

14. Distributive Property
(cont.)

15. Example 4
Use the Distributive Property to find 20(102) mentally.
20(102) = 20(100 + 2) Think of 102 as 100 + 2
20(100 + 2) = 20(100) + 20(2) Use Distributive Property
= 2000 + 40 Multiply
= 2,040 Add

16. Example 5
You have 3 friends and want to give each friend 6
cupcakes, 5 cookies, and 4 brownies. How many baked
goods will you have all together?
3(6+5+4)
3(6) + 3(5) + 3(4)
18 + 15 + 12
= 45 baked goods

17.  = Cookies  = Brownies  = Cupcakes
Friend 1:   
Friend 2:   
Friend 3:   
Total:

 = 45 baked goods
Example 5 (cont.)
We can also use mathematical models to
demonstrate the distributive property.

18. Practice Problems
1. 3(6+7) = ? 3(6) + 3(7) = 18 + 21 = 39
2. 4(22+3) = ? 4(22) + 4(3) = 88 + 12 = 100
3. 6(b+5) = ? 6(b) + 6(5) = 6b + 30
4. 9(2h-1) = ? 9(2h) – 9(1) = 18h - 9
5. 3(5-3w) = ? 3(5) – 3(3w) = 15 – 9w

19. Practice Problems (Cont.)
6. Suppose your friend wrote 7(2m+t) = 14m + t.
What error did your friend make? What is the
correct answer?
He or she forgot to distribute the 7 to the variable t.
The correct answer should be:
7(2m) + 7(t) = 14m + 7t

20. Picture Citations:
Light Bulb Guy Picture (Slide 2) -
http://www.cascadewellnessclinic.com/articles/2003art/0311art.shtml
Shopping Bag Picture (Slide 5) –
http://www.education.vic.gov.au/studentlearning/teachingresources/maths/mathscon
tinuum/structure/st275ma.htm
Distributive Arrow picture (Slide 14) - http://www.coolmath.com/reference/math-
dictionary-D.html
Distributive Property Balance (Slide 13) -
http://www.leslienettling.com/6thNewsletters/6thSep8-06.htm

21. Content Citations
Badur, Michalina Central Michigan University student
Davison, David M., Marsha S. Landau, Leah McCracken, and Linda Thompson.
Prentice Hall Pre-algebra: Tools for a Changing World. Upper Saddle
River, NJ: Prentice Hall, 2001. Print.