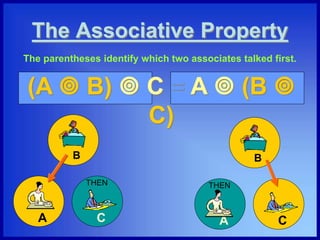
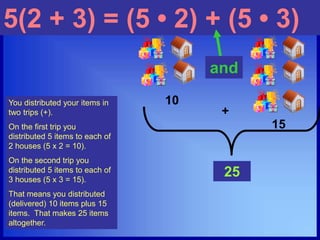
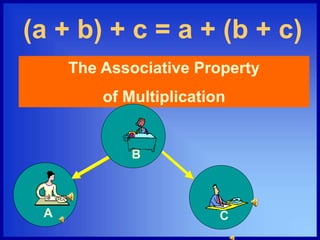
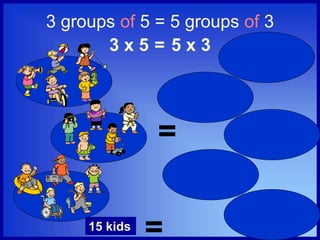The document discusses the five properties of multiplication: the commutative property, the associative property, the identity property, the zero property, and the distributive property. It provides examples and explanations of each property using words and mathematical expressions. For example, it explains that the commutative property states that a × b = b × a, and the identity property indicates that any number multiplied by 1 remains the same number.

1. Multiplication
Properties

2. Do you remember these Properties of Addition?
Commutative Property of Addition
The numbers move around
a + b = b + a
Associative Property of Addition
Grouping with parentheses
(a + b) + c = a + (b + c)
Identity Property of Addition
The identity of the problem does not change
a + 0 = a

3. In multiplication, you will see these
same properties, plus 2 more…

4. Five Properties of Multiplication
These are the basically the same as
addition
Commutative
Associative
Identity
These belong to multiplication only
Zero
Distributive

5. Let’s review the addition
properties— from the
multiplicative perspective…
Multiplicative (Do you see most of the word “multiply” in this word?

6. Property #1
The Commutative Property
of Multiplication

7. The Commutative Property
Background
The word commutative comes from the
verb “to commute.”
Commuting means changing, replacing,
exchanging, switching places, trading
places
People who travel back and forth to
work are called commuters.

8. The Commutative Property
A • B = B • A

9. Here is another example…

10. 3 groups of 5 = 5 groups of 3
=
15 kids
=15 kids
3 x 5 5 x 3=

11. What commutative means to
multiplication…
3 groups of 5 = 5 groups of 3
3 • 5 = 5 • 3
a • b = b • a
Remember… in
Lesson 1-11 we said
that the word “of”
means multiply

12. Property #2
The Associative Property
of Multiplication

13. The Associative Property
Background
The word associative comes from the
verb “to associate.”
Associate means connected, joined, or
related
People who work together are called
associates.
They are joined together by business, and
they have to talk to one another.

14. A C
B
Here are three associates.
B calls A first He calls C
last
If he called C first,
then called A, would
it have made a
difference?

15. (The Role of Parentheses)
In math, we use parentheses to show groups.
In the order of operations, the numbers and
operations in parentheses are done first.
(PEMDAS)
So….

16. The Associative Property
(A  B)  C = A  (B 
C)
A C
B
A C
B
THEN THEN
The parentheses identify which two associates talked first.

17. Property #3
The Identity Property
of Multiplication

18. The Identity Property
I am me!
You cannot change
My identity!

19. One is the only number
you can multiply
something by and see no
change.

20. Identity Property of Multiplication
a x 1 = a
x 1 =

21. Identity Property of Multiplication
a x 1 = a
x 1 =
x 1 =
x 1 =

22. These are 3 of the Properties of Multiplication
Commutative Property of Multiplication
The numbers move around
a • b = b • a
Associative Property of Multiplication
Grouping with parentheses
(a • b) • c = a • (b • c)
Identity Property of Multiplication
The identity of the problem does not change
a • 1 = a

23. There are two more properties
which are unique to multiplication
The Zero Property
The Distributive Property

24. Property #4
The Zero Property of Multiplication

25. The Zero Property of Multiplication
This looks like a mixture of the identity
property of addition and the identity
property of multiplication…
Be careful not to mix them up!

26. The Zero Property
Any time you multiply a number by zero,
your answer is zero! If I have 2
pockets with NO
money in them,
then I have NO
money!
2 • 0 = 0
The

27. Property #5
The Distributive Property
of Multiplication

28. The Distributive Property
Background
The word distributive comes from the
verb “to distribute.”
Distributing refers to passing things out or
delivering things to people

29. The Distributive Property
a(b + c) = (a • b) + (a • c)
A times the sum of b and c = a times b plus a times c
Let’s plug in some numbers first.
Remember that to distribute means delivering items, or handing them out.
Here is how this property works:
5(2 + 3) = (5 • 2) + (5 • 3)

30. 5(2 + 3) = (5 • 2) + (5 • 3)
You went to two houses on one street and three houses on a different street.
Every family bought 5 items!
You went to two houses on one street and three houses on a different street. Every family bought 5 items!
You have sold many items for the RCMS fundraiser!

31. You will be distributing 5 items to each house.
1
2
3
4
5

32. 5(2 + 3) = (5 • 2) + (5 • 3)
You distributed (delivered) these all in one trip.
There are (2+3) five houses all together.
You need to deliver 5 gifts to each house.
You need to put 25 items on your wagon at
one time.
5 items x 5 houses = 25 items all together

33. 5(2 + 3) = (5 • 2) + (5 • 3)
You distributed your items in
two trips (+).
On the first trip you
distributed 5 items to each of
2 houses (5 x 2 = 10).
On the second trip you
distributed 5 items to each of
3 houses (5 x 3 = 15).
That means you distributed
(delivered) 10 items plus 15
items. That makes 25 items
altogether.
and
10
15
+
25

34. The Distributive Property
DISTRIBUTION CENTER
Make 1 trip. You have 5 houses. You
need to bring 5 items to each house.
You need 25 items on your wagon.
5(2 + 3)

35. The Distributive Property
DISTRIBUTION CENTER
Make 2 trips. You have 2 houses for
your first trip and you need to bring 5
items to each house. You have 3
houses on your second trip and need
to bring 5 items to each house. When
your second trip is over, you will have
distributed 25 items.
(5 • 2) + (5 •3)

36. How do I tell the properties apart?
Commutative
Numbers switch places
Associative
Parentheses on both sides
Only multiplication on each side
Identity
Multiply by 1
Zero Property
Multiply by zero
Distributive
Parentheses on each side
One side has a multiplication sign AND a plus sign

37. Let’s practice !
Look at the problem.
Identify which property it represents.

38. 4(5 + 6) = (4 • 5) + (4 • 6)
The Distributive Property
of Multiplication
•3 numbers on one side—4 on the other
•Multiplication AND addition
•3 sets of parentheses

39. 987 • 1 = 987
The Identity Property
of Multiplication
•Times 1

40. 3 • 0 = 0
Zero Property of Multiplication
•Times zero

41. (1 • 2) • 3 = 1 • (2 • 3)
The Associative Property of
Multiplication
•Same 3 numbers
•Multiplication only
•2 sets of parentheses

42. 6 • 11 = 11 • 6
The Commutative Property
of Multiplication
•Same 2 numbers
•Numbers switched places

43. 9 • 7 = 7 • 9
The Commutative Property
of Multiplication
•Same 2 numbers
•Numbers switched places

44. 12 • 0 = 0
Zero Property of Multiplication
•Times zero

45. (9 • 8) • 7 = 9 • (8 • 7)
The Associative Property of
Multiplication
•Same 3 numbers
•Multiplication only
•2 sets of parentheses

46. 9(8 + 7) = (9 • 8) + (9 • 7)
The Distributive Property
of Multiplication
•3 numbers on one side—4 on the other
•Multiplication AND addition
•3 sets of parentheses

47. 9 • 1 = 9
The Identity Property
of Multiplication
•Times 1

48. a • 1 = a
The Identity Property
of Multiplication

49. a • b = b • a
The Commutative Property
of Multiplication

50. A
(a + b) + c = a + (b + c)
The Associative Property
of Multiplication
C
B

51. a • 0 = 0
The Zero Property
of Multiplication

52. a(b • c) = (a • b) + (a • c)
The Distributive Property
of Multiplication