This document discusses commutative and associative properties in mathematics. The commutative property means the order of numbers does not change the sum or product. The associative property means the grouping of numbers does not change the sum or product. These properties allow mathematical problems to be solved by rearranging or regrouping numbers in efficient ways using mental math strategies.

1. Commutative and
Associative Properties

2. Commutative and Associative Properties
• Properties refer to rules that indicate a standard
procedure or method to be followed.
• A proof is a demonstration of the truth of a
statement in mathematics.
• Properties or rules in mathematics are the result
from testing the truth or validity of something by
experiment or trial to establish a proof.
• Therefore, every mathematical problem from the
easiest to the more complex can be solved by
following step by step procedures that are
identified as mathematical properties.

3. Commutative and Associative Properties
• Commutative Property means changing the order
in which you add or subtract numbers does not
change the sum or product.
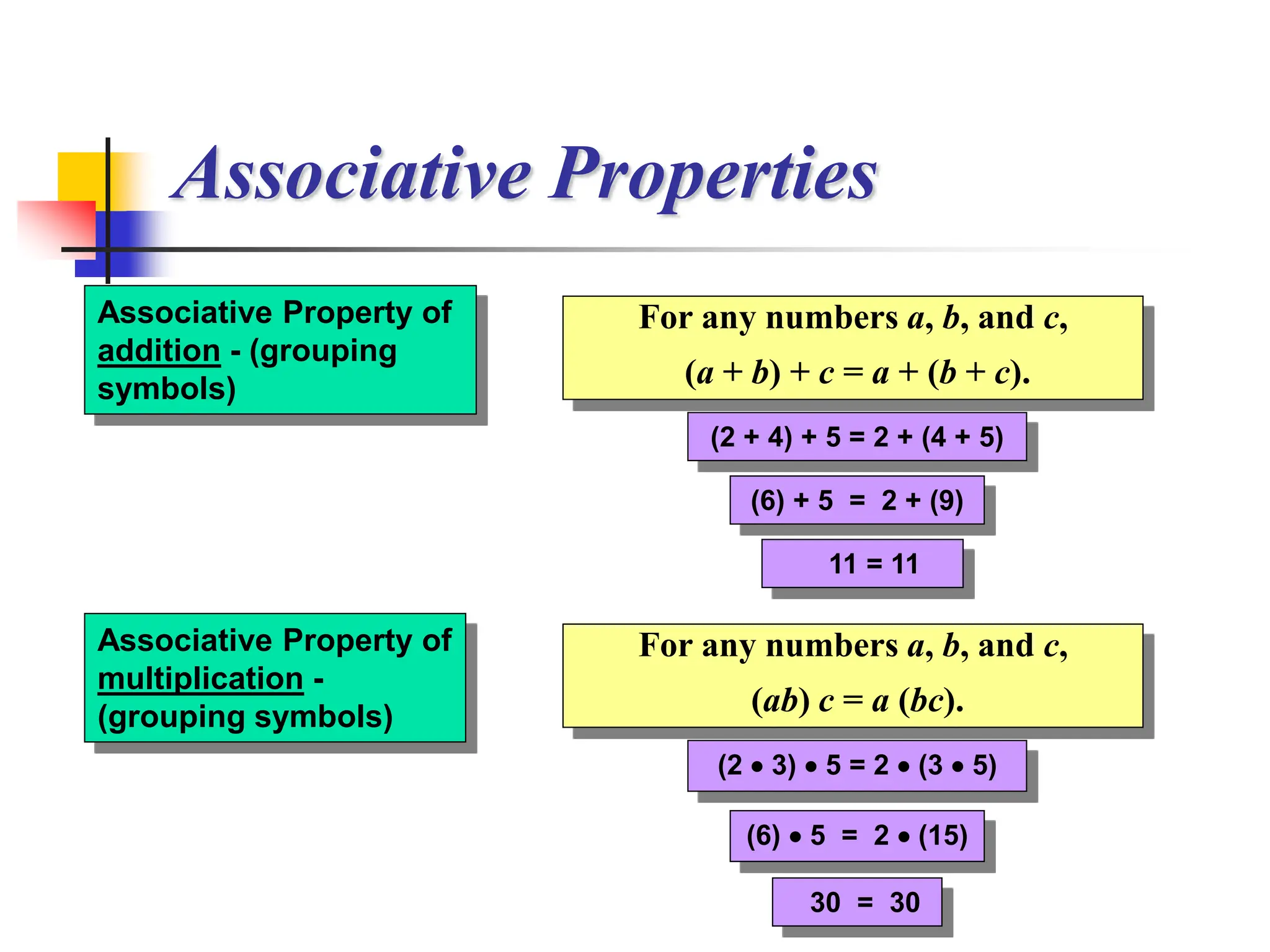
• Associative Property means changing the
grouping of numbers when adding or multiplying
does not change their sum or product.
• Grouping symbols are typically parentheses (),but
can include brackets [] or Braces {}.

4. Commutative Property
of addition - (Order)
Commutative Property
of multiplication -
(order)
For any numbers a and b , a + b = b + a.
For any numbers a and b , a  b = b  a.
45 + 5 = 5 + 45
6  8 = 8  6
50 = 50
48 = 48
Commutative Properties

5. Associative Property of
addition - (grouping
symbols)
Associative Property of
multiplication -
(grouping symbols)
For any numbers a, b, and c,
(a + b) + c = a + (b + c).
For any numbers a, b, and c,
(ab) c = a (bc).
(2 + 4) + 5 = 2 + (4 + 5)
(2  3)  5 = 2  (3  5)
(6) + 5 = 2 + (9)
11 = 11
(6)  5 = 2  (15)
30 = 30
Associative Properties

6. Evaluate: 18 + 13 + 16 + 27 + 22 + 24
Rewrite the problem by grouping numbers that can be formed easily.
(Associative property) This process may change the order in which the
original problem was introduced. (Commutative property)
(18 + 22) + (16 + 24) + (13 + 27)
(40) + (40) + (40) = 120
Commutative and Associative Properties
• Commutative and Associative properties are very helpful
to solve problems using mental math strategies.

7. Evaluate: 4  7  25
Rewrite the problem by changing the order in which the original
problem was introduced. (Commutative property) Group numbers that
can be formed easily. (Associative property)
4  25  7
(4  25)  7
(100)  7 = 700
Commutative and Associative Properties
• Commutative and Associative properties are very helpful
to solve problems using mental math strategies.