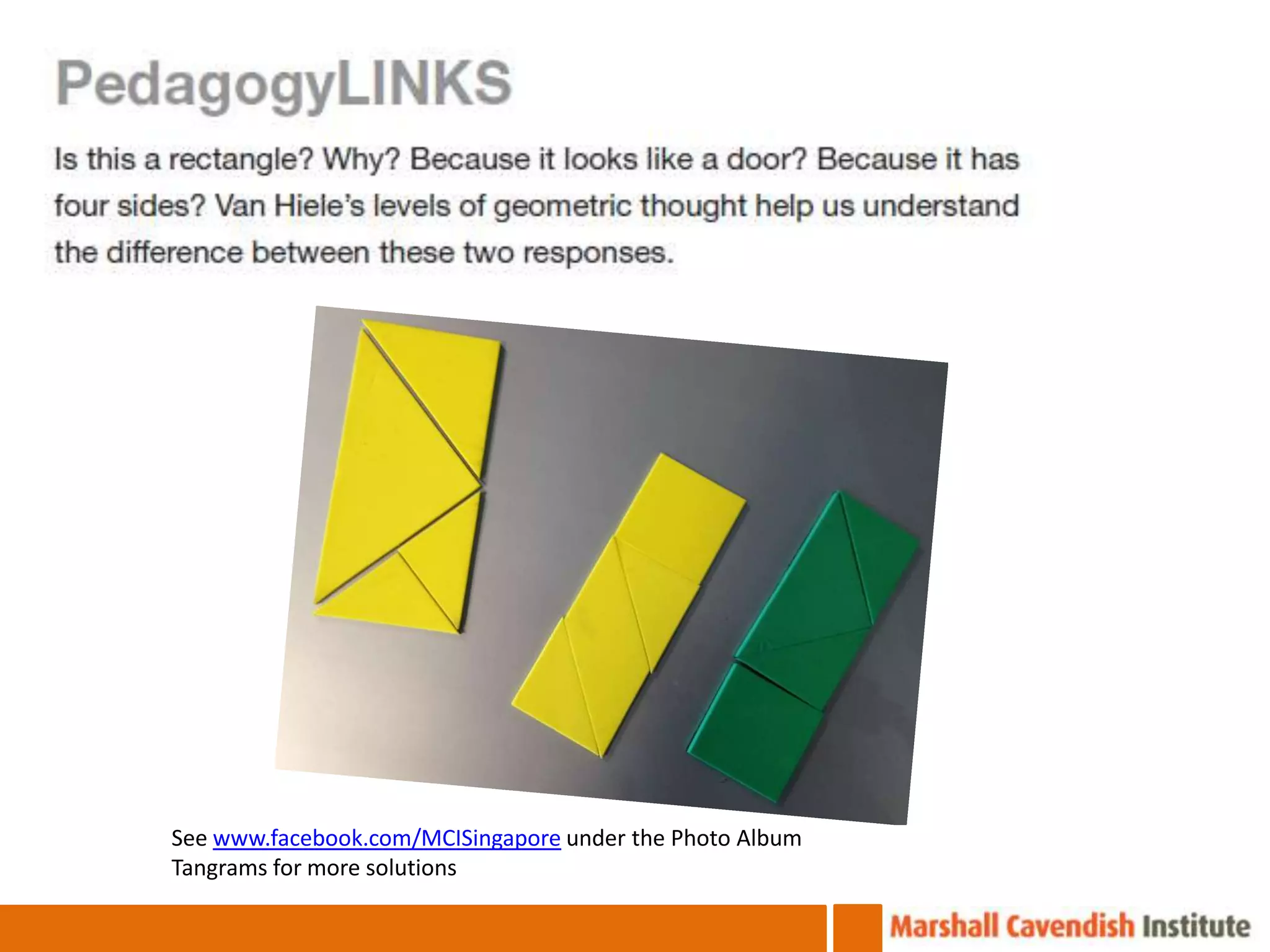
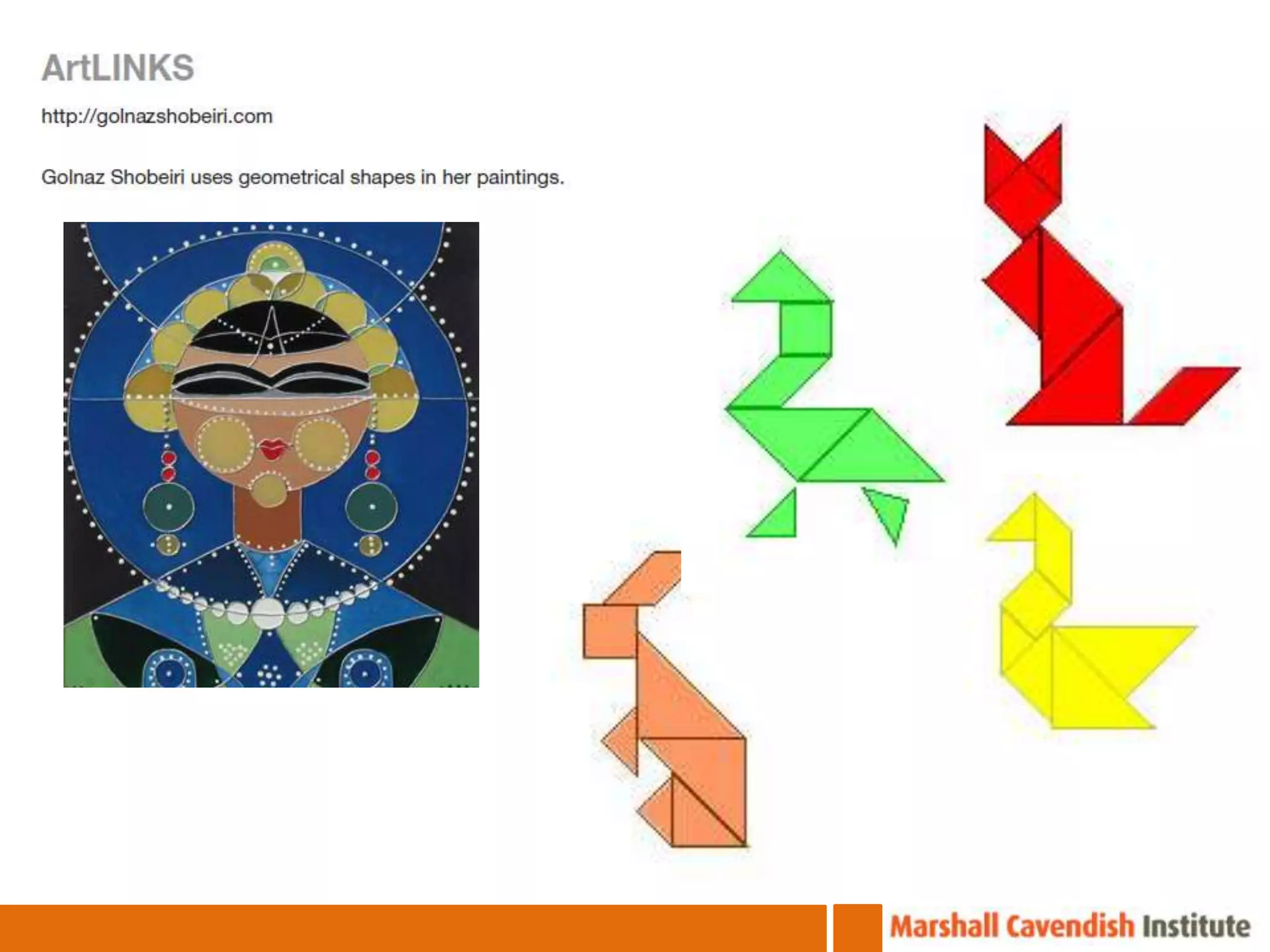
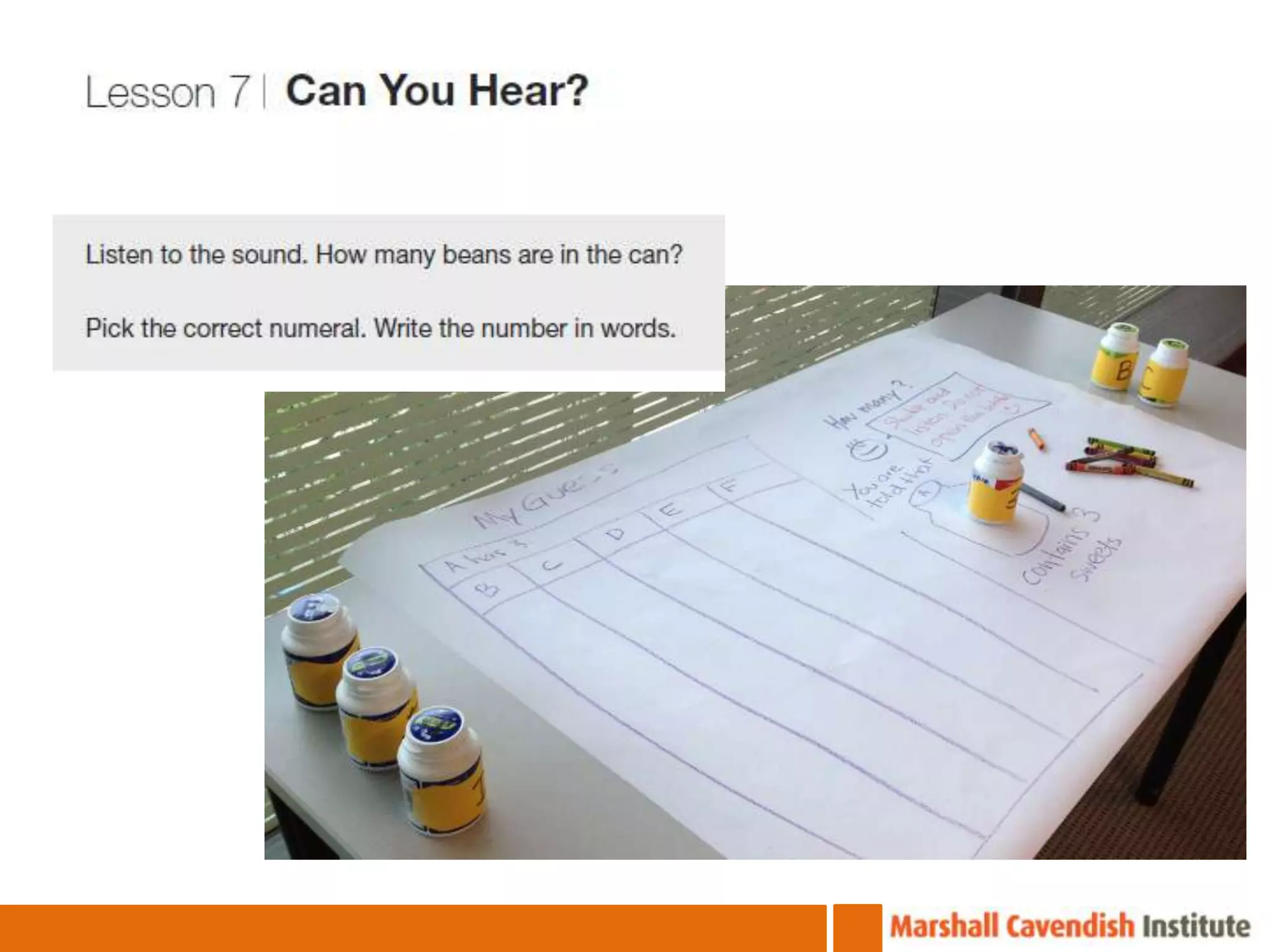
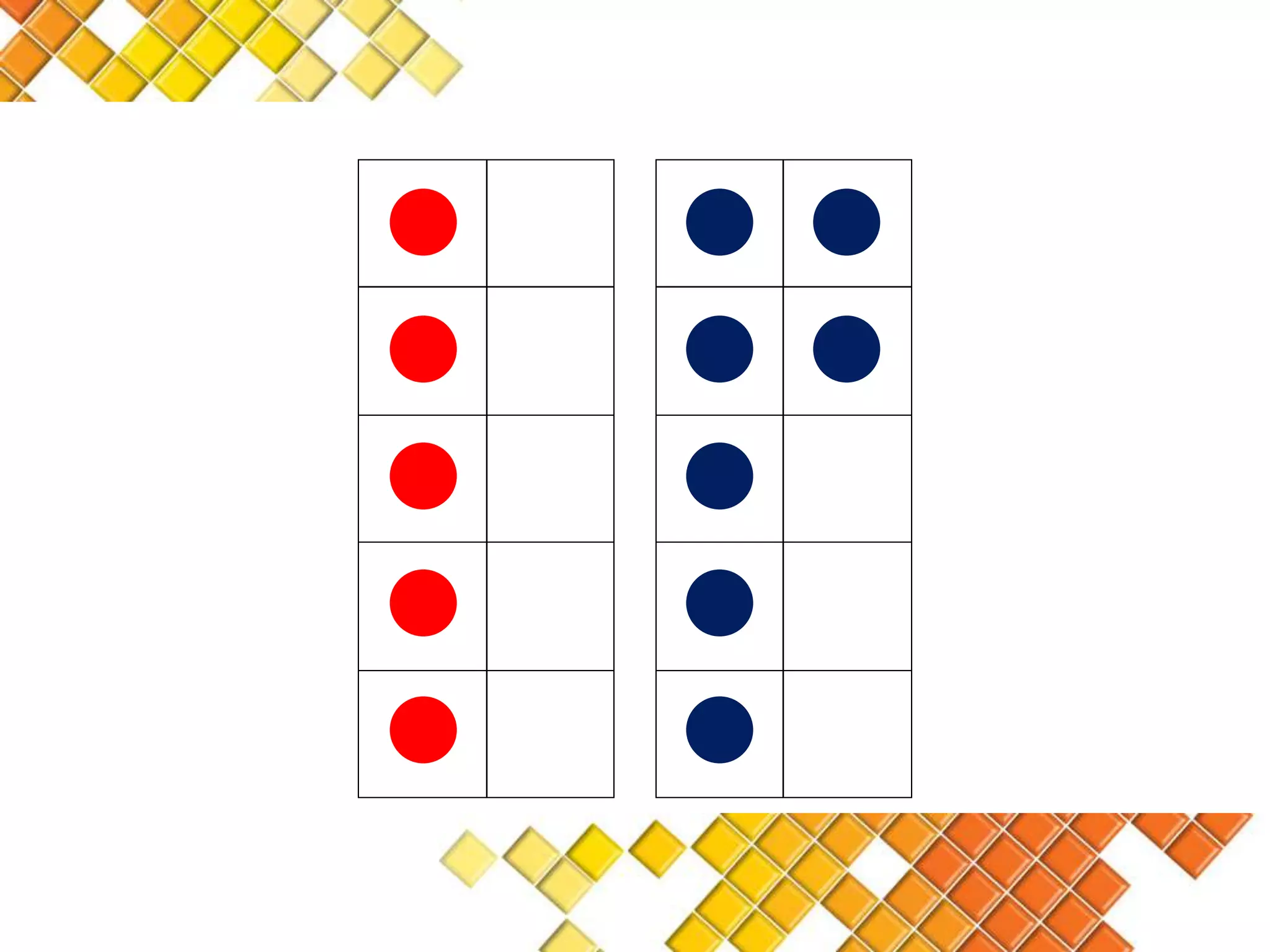
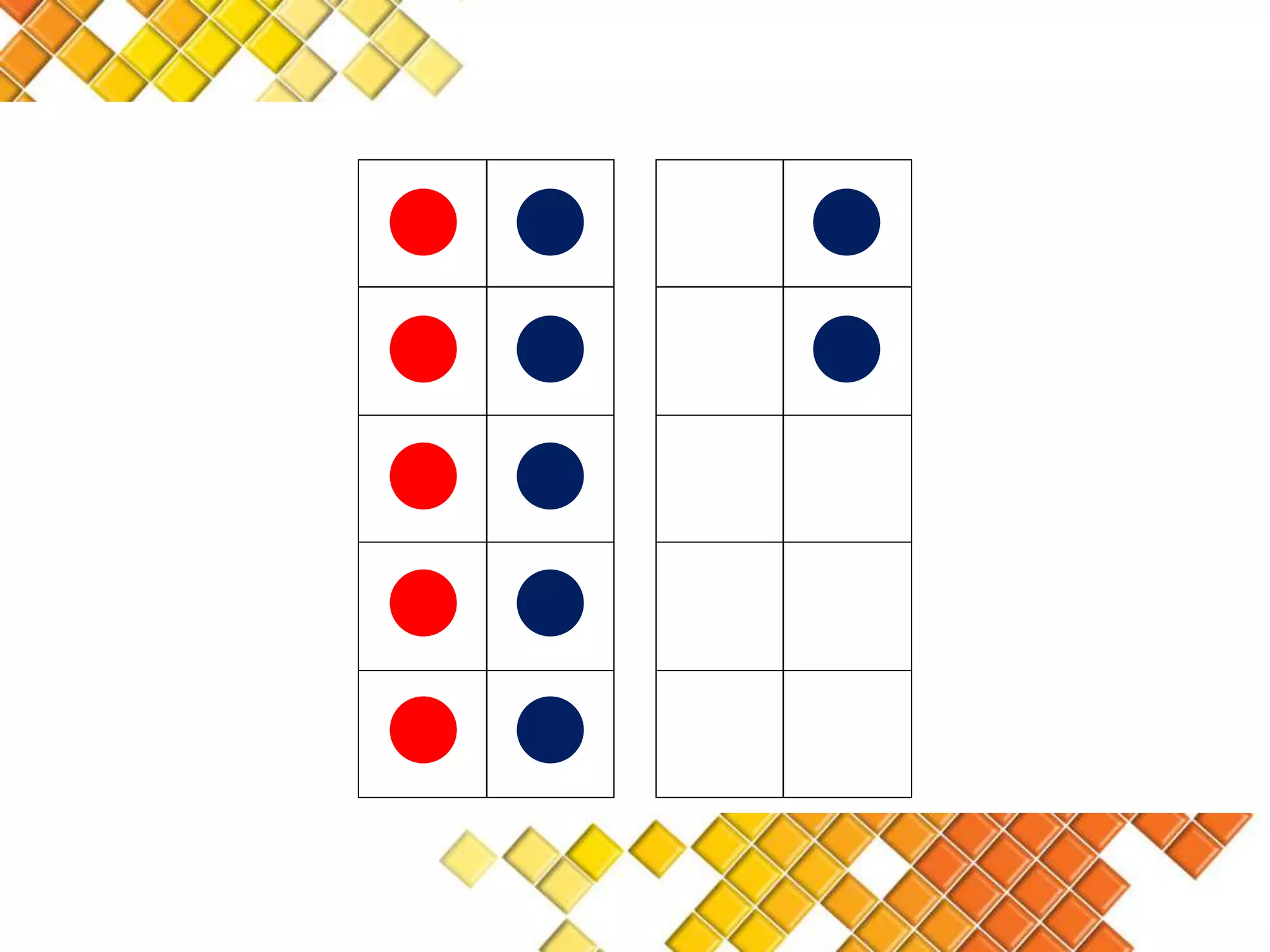
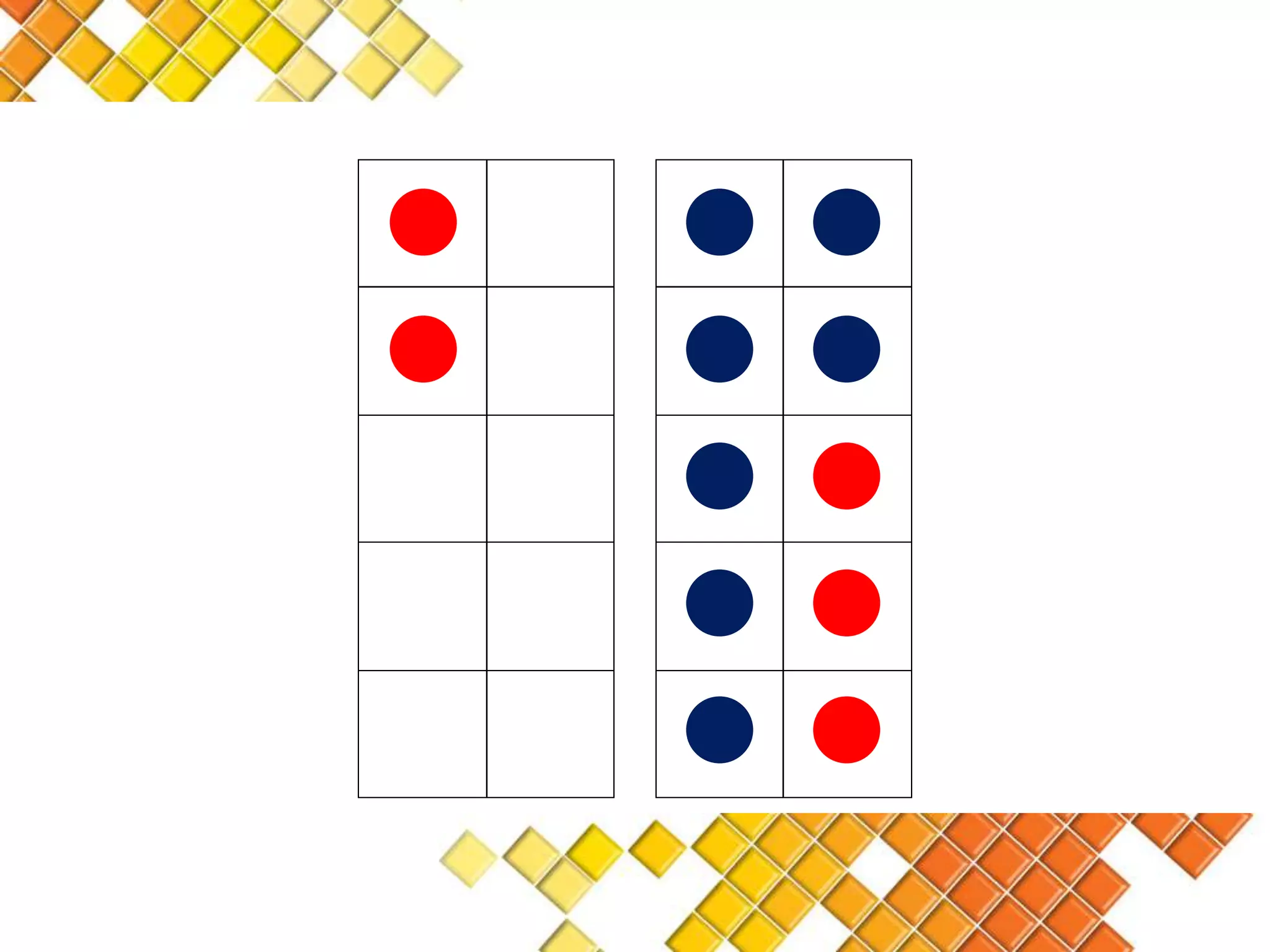
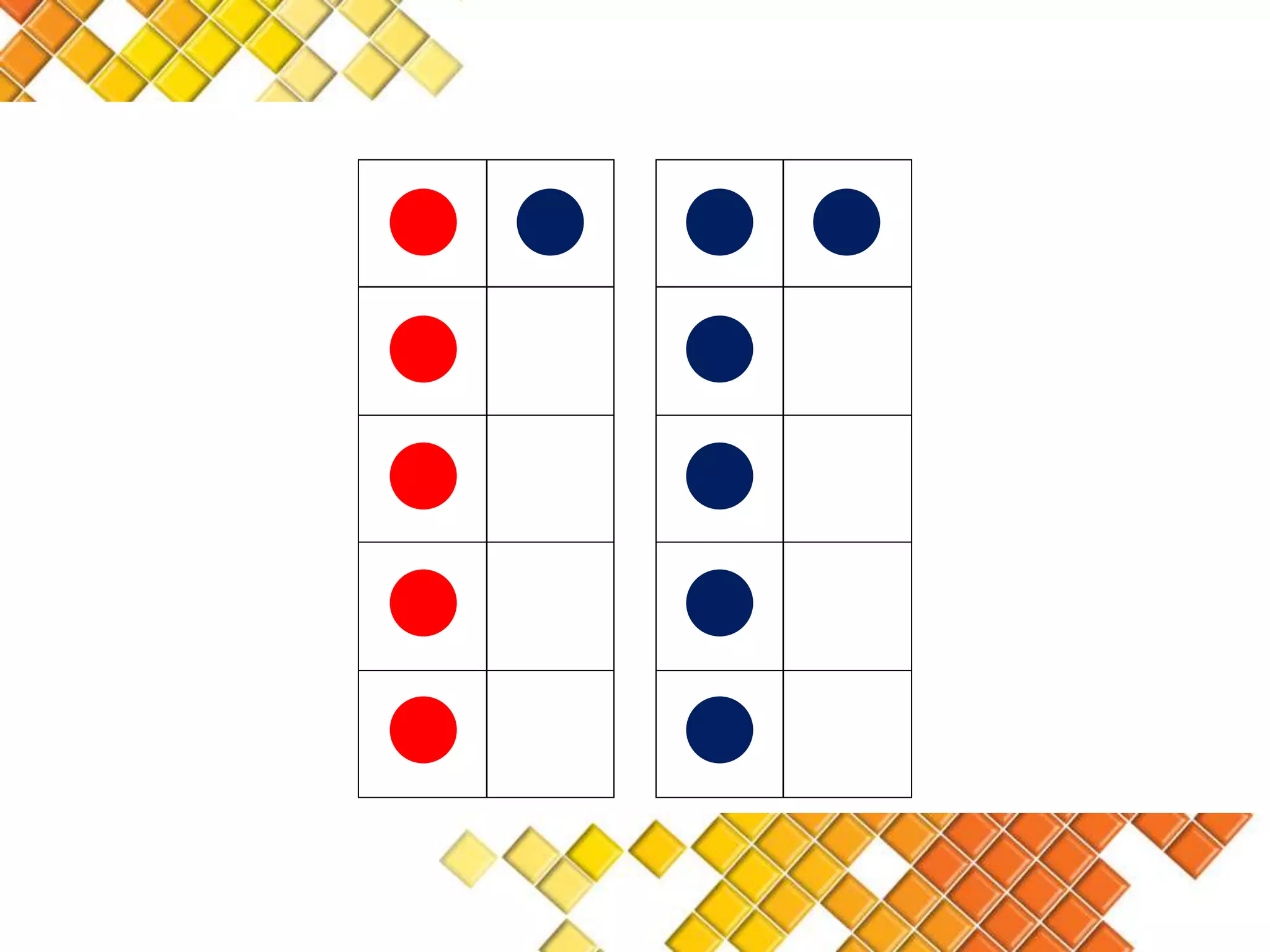
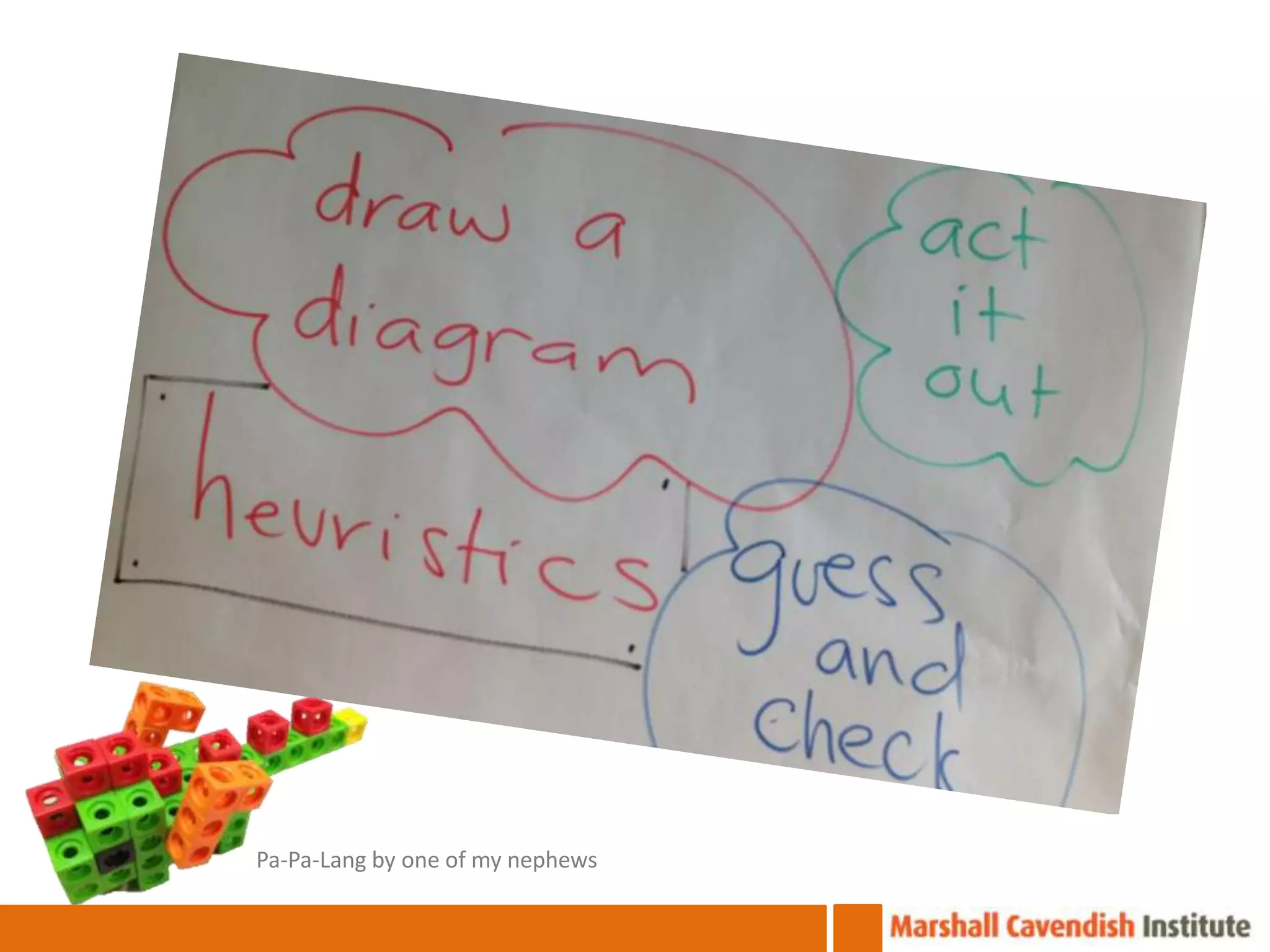
The document discusses the van Hiele model of geometric thinking, detailing its five developmental levels from visualization to rigor, with instructional implications for each. It emphasizes the importance of using concrete materials and engaging activities to enhance geometric understanding and visualization skills in pre-school education. Additionally, the document provides examples of counting strategies and activities to support the development of numerical understanding.

1. Organizer
Pre-School Education Unit
Ministry of Education, Singapore

2. Slides are available at Lecturer
www.i-teach-k.blogspot.com Yeap Ban Har
www.facebook.com/MCISingapore yeapbanhar@gmail.com

4. introduction
from 1992 to 2013

7. “Mathematics is an excellent
vehicle for the development
and improvement of a person’s
intellectual competencies”
Singapore Ministry of Education 2006

8. visualization

9. looking
for
patterns

10. number
sense

12. what
to teach

13. how to
teach

15. Use 3 pieces. Make a rectangle.

16. See www.facebook.com/MCISingapore under the Photo Album
Tangrams for more solutions

19. Development of
Geometric Thinking
van Hiele Model of Geometric Thinking
There are 5 levels:
• Level 0: Visualisation
• Level 1: Analysis
• Level 2: Informal Deduction
• Level 3: Deduction
• Level 4: Rigour
The levels are sequential – must start at the basic level.

20. Level 0: Visualisation
• Recognise the appearance of the shapes (look
sort of alike)
• Properties are incidental to the shape
(implicit)
“A square is a square because it looks like a
square.”

21. Implications for Instruction
Level 0: Visualisation
• Provide concrete materials that can be manipulated
• Include different and varied examples of shapes
• Involve lots of sorting, identifying, and describing of
various shapes
• Provide opportunities to build, make, draw, put
together and take apart shapes

22. Level 1: Analysis
• More aware of the properties of a shape than
to its appearance
• Use properties to define categories of shapes
(able to list the properties but not the
relationships among the properties)

23. Implications for Instruction
Level 1: Informal Deduction
• Engage in the same activities as level 0 but the focus
of the activities should be on the properties of the
shapes, not identification
• Classify shapes by properties
• Derive generalisation by studying examples
• Use appropriate vocabulary

24. Level 2: Informal Deduction
• Understand the relation of properties within
and among figures
“A square is a rectangle, a rectangle is
parallelogram which is also a quadrilateral.”

25. Level 3: Formal Deduction
• Construct proofs to determine the truth of a
mathematic statements
Level 4: Rigour
• Highly abstract form of geometric thought

26. Summary
 Understand the importance of visualisation and
geometric thinking (van Hiele model of geometric
thinking )
 Use activities to reinforce visualisation skills
• Tangram activity
• Grandfather Tang’s story
• Create your own picture

27. Ordinal, Cardinal & Nominal
Numbers

29. • Cardinal Number
• Ordinal Number
• Nominal Number
• Measurement Number
Siti
Michael
John

30. ordinal
number

32. Problem
Arrange the ten cards so
that you can do what is
shown to you.

33. Method 1 – by drawing

34. Method 2 – by using the cards

35. Scarsdale Teachers’ Institute, New York

37. rational
counting

40. addition
• strategies
Count All
• Count On
• Count On + Commutative Property
• Make Ten
• Number Facts (1 + 1 to 9 + 9)

45. These two players with cards on their I see 8 and 5
forehead cannot see their own card but so I should
can see the other person’s card. The goal say the sum. 13
is to say what number is on her own
forehead.
Santiago, Chile

46. Manila, The Philippines

48. What if a child is already proficient in counting – which is the main
purpose of the activity? They may be asked to observe a pattern to
suggest a winning strategy.

49. Ministry of Education Singapore

51. Pa-Pa-Lang by one of my nephews