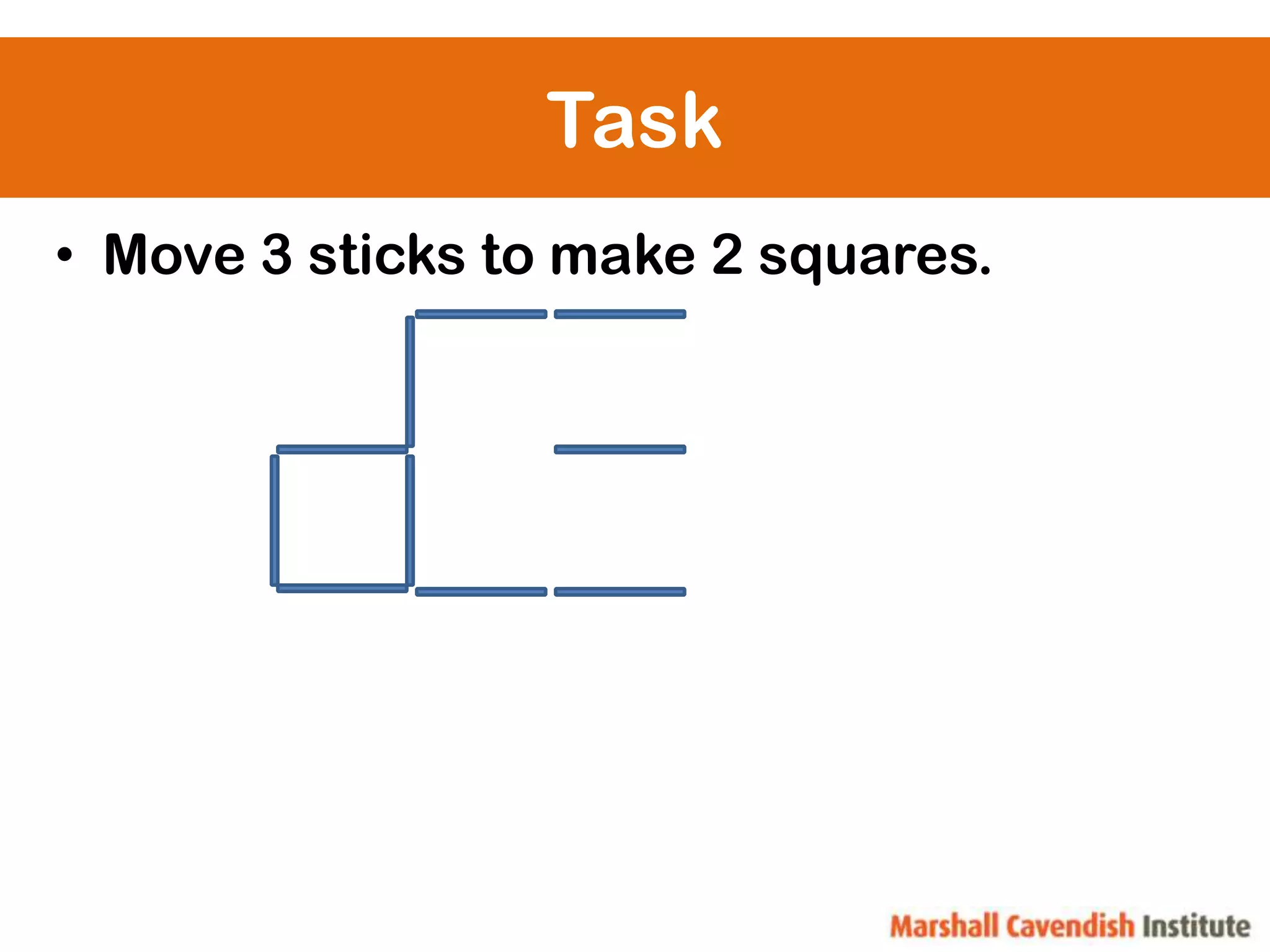
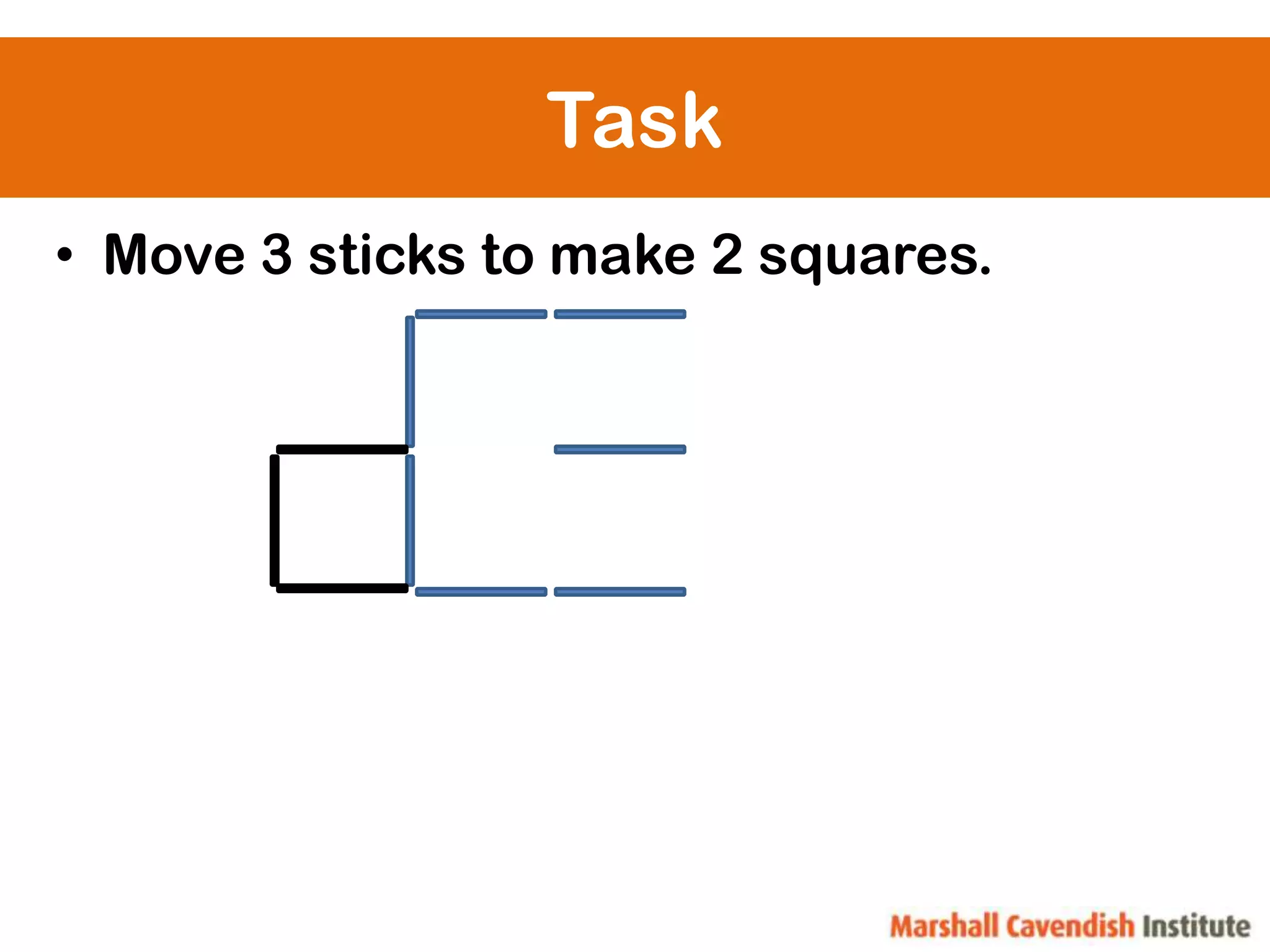
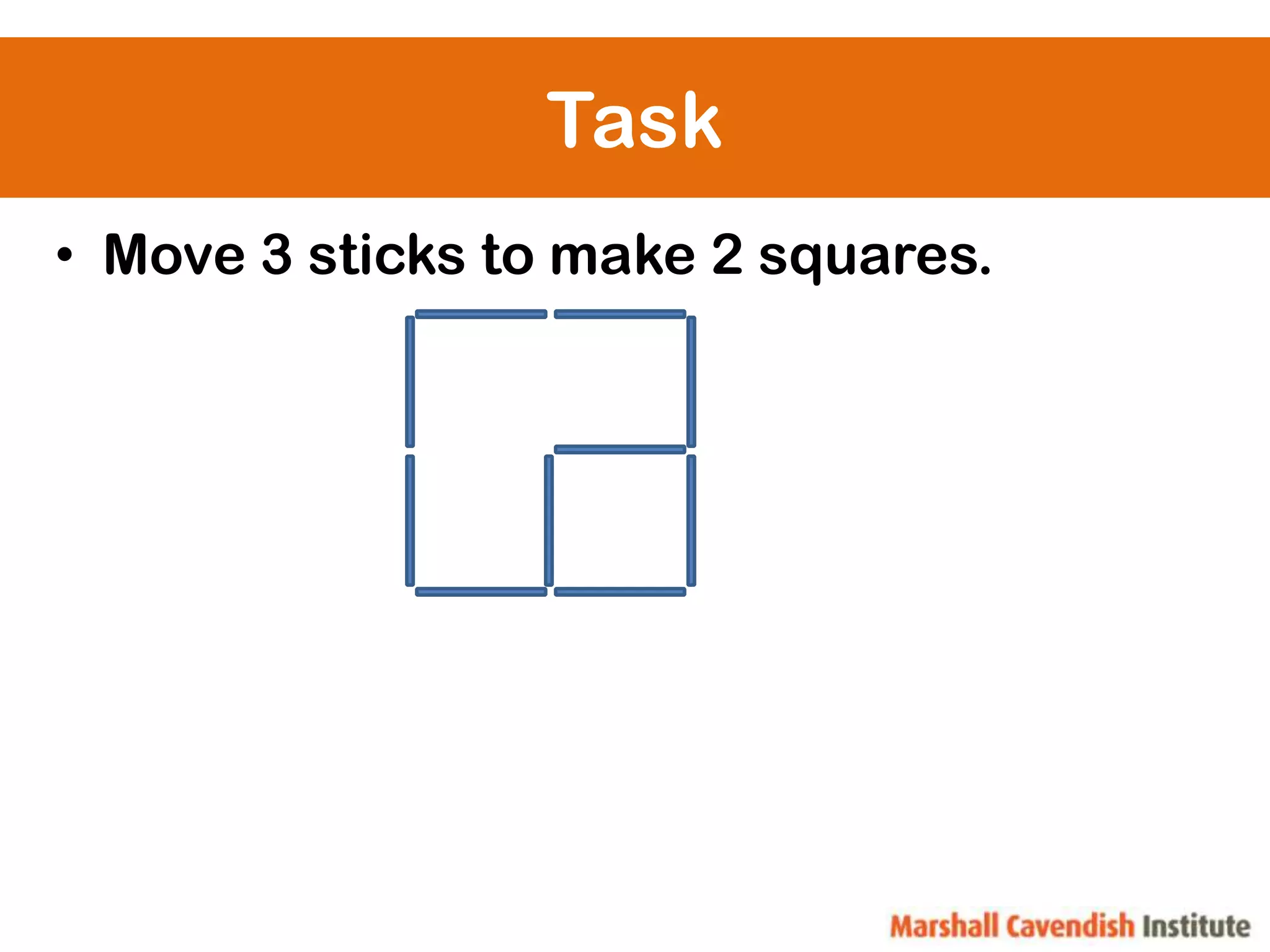
Here are the steps: 1. Think of two digits, e.g. 3 and 5 2. Make the largest number: 53 3. Make the smallest number: 35 4. Find the difference: 53 - 35 = 18 I notice that the difference is always 18 no matter what two digits are chosen. This is because when forming the largest and smallest numbers from two digits, the ones digit remains the same while the tens digit changes. So the difference is always 10 * (tens digit of largest number - tens digit of smallest number) = 10 * (1 - 0) = 18.

2. This course focuses on the WHAT and HOW of numeracy
programmes in early childhood education. You will complete four
modules in this course.
By the end of this course, you will learn
• selected key content areas such as ordinal numbers, cardinal
numbers (counting), addition and subtraction, measurements
and geometry
• the importance of visualization, generalization and number
sense
• the need to include ‘soft’ skills such as communication and
metacognition, creativity and curiosity, and so on
• strategies
• learning theories

3. Visualization
Shapes & Geometry
INSTRUCTOR
Peggy Foo
Marshall Cavendish Institute

4. Spatial Visualisation
• It involves having images of objects
• Spatial visualisation and geometry are
interdependent (learning of one area will lead
to the other)

5. Development of
Geometric Thinking
van Hiele Model of Geometric Thinking
There are 5 levels:
• Level 0: Visualisation
• Level 1: Analysis
• Level 2: Informal Deduction
• Level 3: Deduction
• Level 4: Rigour
The levels are sequential – must start at the basic level

6. Level 0: Visualisation
• Recognise the appearance of the shapes (look
sort of alike)
• Properties are incidental to the shape
(implicit)
“A square is a square because it looks like a
square” i.e. appearance of the shape

7. Implications for Instruction
Level 0: Visualisation
• Provide concrete materials that can be manipulated
• Include different and varied examples of shapes
• Involve lots of sorting, identifying, and describing of
various shapes
• Provide opportunities to build, make, draw, put
together and take apart shapes

8. Level 1: Analysis
• More aware of the properties of a shape than
to its appearance
• Use properties to define categories of shapes
(able to list the properties but not the
relationships among the properties)

9. Implications for Instruction
Level 1: Informal Deduction
• Engage in the same activities as level 0 but the focus
of the activities should be on the properties of the
shapes, not identification
• Classify shapes by properties
• Derive generalisation by studying examples
• Use appropriate vocabulary

10. Level 2: Informal Deduction
• Understand the relation of properties within
and among figures
• Example: a square is a rectangle, a rectangle is
parallelogram which is also a quadrilateral

11. Level 3: Formal Deduction
• Construct proofs to determine the truth of a
mathematic statements

12. Level 4: Rigour
• Highly abstract form of geometric thought

13. Summary
 Understand the importance of visualisation and
geometric thinking (van Hiele model of geometric
thinking )
 Use activities to reinforce visualisation skills
• Tangram activity (manipulate and identify
geometric shape)
• Grandfather Tang’s Story / Create your own
picture (arrange, construct, describe in your own
words)

14. Conservation of
Numbers
INSTRUCTOR
Peggy Foo
Marshall Cavendish Institute

15. Objectives
Participants will be able to:
• Understand the importance of conservation of
numbers
• Study a lesson (video) on a conservation task

16. Conservation of Numbers
• The number of a set remains the same even if
the items of the set are rearranged (Piaget, 1952)
• Basis of number knowledge
• Based on understanding the concept of equality
and one to one correspondence
• Reveal/ assess children’s knowledge of numbers

17. Responses
Number Conservation by Counting:
• I counted them
Number Conservation by Justification:
• Nothing is added or taken away
• I can put them back in the same position so
they look like as they did before

18. Conservation Task
• Using 4 cubes, make as many different
structures as you can

19. Learning points
• What can we achieve using conservation
tasks?
Enhance visualisation skills by constructing different
structures and sorting / classifying the structures
Enhance reasoning and communication skills when asked
to justify one’s responses

20. Summary
• Importance of conservation of numbers
(basis of number knowledge, start with
concept of equality and one-to-one
correspondence)
• Aspects of lesson which support
visualisation and reasoning skills

21. Ordinal and Cardinal
Numbers
INSTRUCTOR
Yeap Ban Har
Marshall Cavendish Institute

22. B A N H A R

24. • Cardinal Number
• Ordinal Number
• Measurement Number
Siti
Michael
John

27. Problem
Rearrange the sticks to
show a given number
of squares.
Wellington Primary School

28. Task Lesson Study Problem
Wellington Primary School
• Move 3 sticks to make 3 squares.

29. Task
• Move 3 sticks to make 3 squares.

30. Task
• Move 3 sticks to make 3 squares.

31. Task
• Move 3 sticks to make 2 squares.

32. Task
• Move 3 sticks to make 2 squares.

33. Task
• Move 3 sticks to make 2 squares.

35. Problem
Arrange the ten cards so
that you can do what is
shown to you.

36. Method 1 – by drawing

37. Method 2 – by using the cards

38. Scarsdale Teachers’ Institute, New York

46. Think of two digits. Make
the largest number. Make
the smallest number. Find
the difference. What do
you notice?