Download as PDF, PPTX
Uploaded byJimmy Keng
Seoul Foreign School Plenary Session
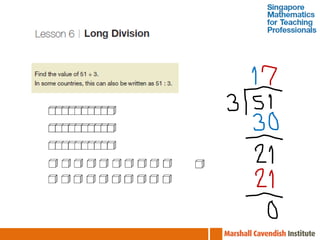
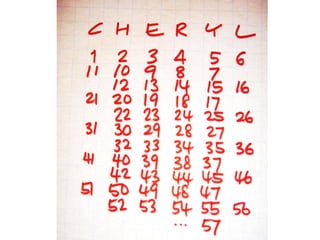
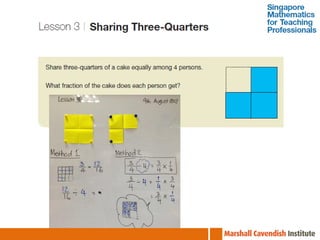
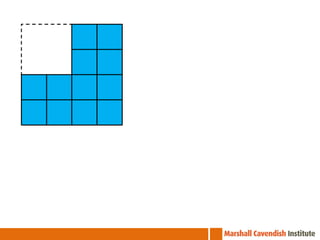
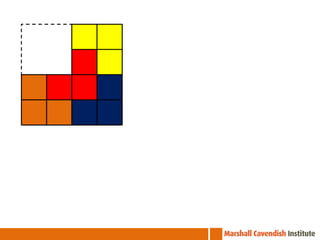
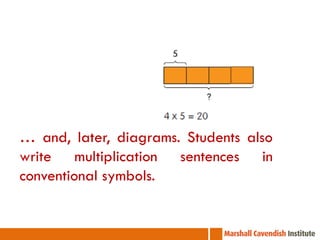
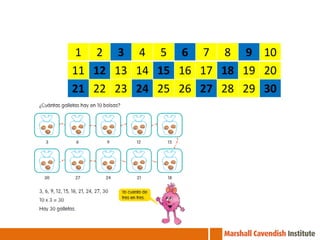
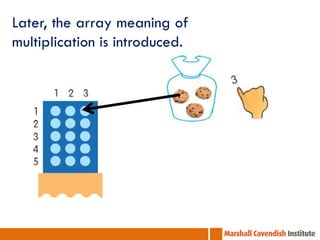
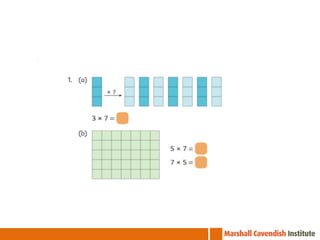
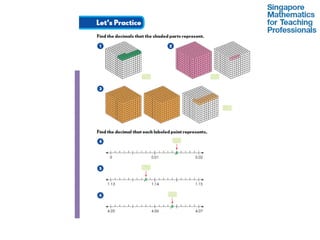
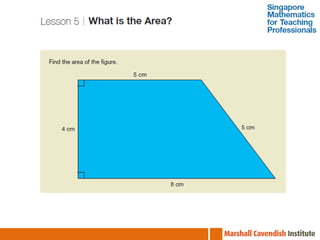
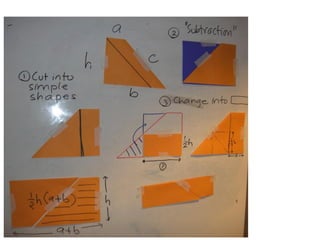
The document outlines a professional development course on Singapore Mathematics, emphasizing its distinct approach to problem-solving and conceptual understanding through the CPA (Concrete-Pictorial-Abstract) framework. It discusses various teaching methods, such as the use of bar models and differentiated instruction strategies to engage advanced learners effectively. The course aims to illustrate how these methods facilitate students' understanding of mathematical concepts and improve their problem-solving skills.
More Related Content
Similar to Seoul Foreign School Plenary Session
Seoul Foreign School Plenary Session
- 1. Professional Development Singapore Mathematics Seoul 9 – 11 July 2012 Dr Yeap Ban Har yeapbanhar@gmail.com Marshall Cavendish Institute Singapore Presentation slides are available at www.banhar.blogspot.com MAP101 www.mcinstitute.com.sg www.facebook.com/MCISingapore
- 2. FUNDAMENTALS ofsingapore math Mayflower Primary School, Singapore Slides are available at www.banhar.blogspot.com
- 3. Introduction This course isan overview of Singapore Math. It includes the what and how of teaching mathematics.
- 5. Curriculum document isavailable at http://www.moe.gov.sg/
- 6. THINKING SCHOOLS LEARNING NATION Singapore Ministry of Education 1997
- 7. what is singapore mathematics
- 8. key focus of singapore mathematics
- 9. problem solving
- 10.
- 11. an excellent vehicle for the development &improvement of a person’s intellectual competencies Ministry of Education Singapore 2006
- 12.
- 13. FUNDAMENTALS ofsingapore math Mayflower Primary School, Singapore Slides are available at www.banhar.blogspot.com
- 14. Singapore Math Visualization
- 16. 110 g 180 g 110 g Bella puts 180 g brown sugar on the dish. 290 g
- 17. on an identicaldish 110 g 2 units = 180 g 1 unit = 90 g 180 g 110 g 3 units = 270 g Bella puts 270 g brown sugar on the dish. 290 g
- 19. Singapore Math isbased on the CPA Apporach. Pictorial representations can be more concrete (pictures) or more abstract (diagrams such as bar model). An alternate way to solve the brown sugar problem:
- 20. Singapore Mathematics focuses on the ability to visualize. For example, bar models are used extensively. Bar models were introduced to overcome the pervasive problems students had with word problems – even the basic ones.
- 21. Such word problemsare used to help students Deal with information Handle and clarify ambiguity – one dish or two Develop visualization – bar models are used extensively Practice mental strategies – numbers used are not difficult to compute
- 22. Singapore Math Visualization
- 23. Procedural & Conceptual Understanding Singapore Math places an emphasis on both. Procedures are explained in a conceptual way. For example, long division is seen simply as breaking large numbers into smaller ones before dividing.
- 30. Using number bonds to make sense of long division Differentiated Instruction for advanced Over- learners – how does one get the result emphasizing of 51 3 from 60 3. procedural Balancing knowledge procedural knowledge with conceptual understanding
- 31. Singapore Math Patterns &Generalization
- 33. Task Extension for AdvancedLearners
- 34. C H E R Y L
- 35. C H E R Y L 1
- 36. C H E R Y L 2
- 37. C H E R Y L 3
- 38. C H E R Y L 4
- 39. C H E R Y L 5
- 40. C H E R Y L 6
- 41. C H E R Y L 7
- 42. C H E R Y L 8
- 43. C H E R Y L 9
- 44. C H E R Y L
- 45. C H E R Y L
- 46. C H E R Y L
- 47. C H E R Y L
- 48. C H E R Y L
- 49. C H E R Y L Which letter is 99?
- 51. Method 1 The positionsof 11, 22, 33 are at C, H, E respectively. Positions of multiples of 11 can be located. Method 4 The position for 99 can be found by writing out all the numbers Method 3 but this is not Numbers ending with 9 efficient are at E. So, 99 is at E method. Method 2 too. The positions of numbers ending with 1 and 6 can be located ta either ends. Thus 91 or 96 can be located. Subsequently, 99 can be located.
- 52. D A VI D
- 54. Method 1 The lettersunder A and I are even. So 99 cannot be there. Method 2 The positions of numbers ending with 9 form a diagonal pattern. Method 3 The numbers under first D increases by 8. Thus 17 + 80 = 97 is under first D. The position for 99 can be worked out. Method 4 The positions of multiples of 8 I is definitely under A. 8 x 12 = 96 is under A. The position of 99 can be worked out. Method 5 Numbers under V is 1 less than multiples of 4. So, 2011 (1 less than 2012) is under V. 99 is less than 100.
- 55. Method 2 The positionsof numbers ending with 9 form a diagonal pattern. The methods were the ones that participants in Chile came up with.
- 56. Another Method In acourse done in December 2010 with a group of Chilean teachers, there was a method that involves division. For Cheryl, it was 99 10. For David, it was 99 8. Are you able to figure out that method?
- 57. Singapore Math Patterns &Generalization
- 58. Singapore Mathematics: Focuson Problem Solving
- 64. CPA Approach basedon Jerome Bruner was used to learn division of fractions – using paper folding and subsequent drawing.
- 66. Singapore Mathematics: Focuson Conceptual Understanding
- 67. Singapore Math Learn NewConcept Through Problem Solving
- 68. Textbook Study Observe thevarious meanings of multiplication from Grade 1 to Grade 3.
- 69. Multiplication Facts We doa case study on multiplication facts. We will see the use of an anchor task to engage students for an extended period of time.
- 74. Strategy 1 Get 3x 4 from 2 x 4 Strategy 2 Doubling Strategy 3 Get 7 x 4 from 2 x 4 and 5 x 4 Strategy 4 Get 9 x 4 from 10 x 4
- 75. Strategy 1 Get 3x 4 from 2 x 4
- 76. Strategy 3 Get 9x 4 from 4 x 4 and 5 x 4 This is essentially the distributive property. Do we introduce the phrase at this point?
- 77. Strategy 2 Doubling
- 78. Strategy 4 Get 9x 4 from 10 x 4
- 79. Unusual Response Get 4x 8 from 4 x 2. Can it be done? Does the number of cups change? Does the number of counters per cup change?
- 80. Differentiated Instruction These areexamples of how the lesson can be differentiated for advanced learners.
- 82. Prior to learningmultiplication, students learn to make equal groups using concrete materials. Marbles is the suggested materials.
- 83. After that theyrepresent these concrete situations using, first, drawings ..
- 84. Open Lesson inChile
- 85. … and, later,diagrams. Students also write multiplication sentences in conventional symbols.
- 86. First, equal groups– three groups of four. Third, four multiplied three times …. Second, array – Three rows of four
- 87. Textbook Study Observe how equal group representation evolves into array and area models. Also observe how the multiplication tables of 3 and 6 are related on the flights of stairs.
- 88. They begin withequal group representation.
- 89. 1 2 34 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
- 90. In Primary 2,students learn multiplication facts of 2, 5, 10 and 3 and 4. In Primary 3, they learn the multiplication facts of 6, 7, 8 and 9.
- 91. Later, the arraymeaning of multiplication is introduced.
- 92. Square tiles aresubsequently used to lead to the area representation of multiplication.
- 97. Open Lesson atBroomfield, Colorado
- 98. Students who werealready good in the skill of multiplying two-digit number with a single-digit number were asked to make observations. They were asked “What do you notice? Are there some digits that cannot be used ta all?”
- 99. Singapore Math Drill-and-Practice Through Problem Solving
- 100.
- 101.
- 103.
- 105. FUNDAMENTALS ofsingapore math The following slides are for additional tasks that are discussed on the second day for Grades 5 – 8 Mayflower Primary School, Singapore Slides are available at www.banhar.blogspot.com
- 114. Marcus gave ¼of his coin collection to his sister and ½ of the remainder to his brother. As a result, Marcus had 18 coins. Find the number of coins in his collection at first. 3 units = 18 8 units = ??? Marcus had 48 coins at first.