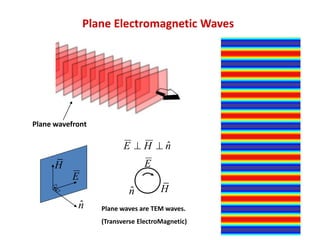
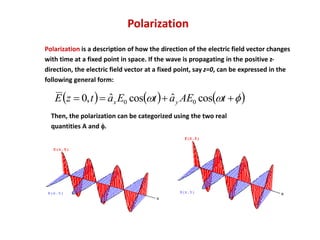
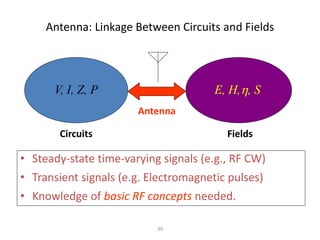
This document discusses different types of antenna jobs and areas of research. It describes three main sectors for antenna jobs: private sector working for consumer electronics companies, defense department/government jobs, and university/research jobs. It provides details on the responsibilities for each type of private sector job and notes that defense and government jobs focus more on research and integration. University/research jobs primarily involve publishing research and involve some teaching. Active areas of antenna research mentioned include meta-materials, electromagnetic solvers, miniaturization, and array optimization.

1. EC6602 ANTENNA AND WAVE
PROPAGATION
M.KRISHNAMOORTHY
Asst.Professor/ECE
GOJAN SCHOOL OF BUSINESS AND
TECHNOLOGY

2. Antennas Fundamentals

3. 3 main sectors of antenna jobs
• Private-Sector Antenna Jobs
• Consumer electronics companies (Research in Motion, Apple, Samsung, HP, etc)
hire antenna engineers to assist in developing their products. The antenna
engineers are responsible for these areas:
• antenna design (including working with product development teams to define
appropriate antenna volumes, geometry, impedance matching etc)
• integration (ensuring the antenna continues to radiate as the product goes from
prototype to production stage, ensuring antenna is manufacturable)
• product testing (which includes defining minimum acceptance levels and
ensuring product quality, setting VSWR specs, etc)
• failure analysis (determining why failed or returned products fail and how this
can be corrected).

4. • Defense Department or Government Jobs
• A big area for antenna engineers is working on
defense programs
• These jobs are less concerned with manufacturability
and antenna design, and more focused on research
and integration. Antenna engineers at defense
companies tend to write a lot of code for antenna or
general electromagnetic analysis.
• Antenna systems on defense aircraft .Antenna
engineers in this world struggle with antenna to
antenna coupling, field of view requirements, making
radomes, so antennas are more aerodynamic, etc.

5. • Research (University) Jobs
• These careers are all about publishing in the journal
IEEE Transactions on Antennas and Propagation. The
positions can be as a professor or as a full-time
researcher. These jobs are almost exclusively in the
University world, but some National Labs also have
research positions where the primary goal is to
publish.

6. • Some active areas of research include:
• Meta-Material Antennas
• Electromagnetic Solver Development (FDTD, MoM, FEM, etc.)
• Antenna Miniaturization
• Antenna Array Optimization (weights, positions, etc)
• Broadband Antennas
• Obtaining these positions is all about publishing. A Ph.D. is a
necessity, and the more conference and journal publications
you have the more likely you are to land a position here.
These jobs typicaly involve some amount of teaching
responsibility, student mentorship, and a fair amount of grant
or proposal writing to obtain funding for your research.

7. Review of Vectors

8. Illustration of components of a force vector
in moving an object.

9. Addition of two vectors.(Head to tail rule)

10. The dot product of two vectors.

11. The cross product of two vectors and the
right-hand rule for determining the
direction of the resultant.

12. 12
Why Do We Need Coordinate
Systems?
• The laws of physics in general are independent of
a particular coordinate system.
• However, application of these laws to obtain the
solution of a particular problem imposes the need
to use a suitable coordinate system.
• It is the shape of the boundary of the problem
that determines the most suitable coordinate
system to use in its solution.

13. Coordinate systems
• In a 3D space, a coordinate system can be specified by the intersection of 3
surfaces.
• An orthogonal coordinate system is defined when these three surfaces are
mutually orthogonal at a point.
A general orthogonal coordinate
system: the unit vectors are mutually
orthogonal
The cross-product of two unit vectors
defines a unit surface, whose unit
vector is the third unit vector.

14. Most commonly used coordinate
systems
(a) – Cartesian; (b) – Cylindrical; (c) – Spherical.
In Cartesian CS, directions of unit vectors are independent of their positions;
In Cylindrical and Spherical systems, directions of unit vectors depend on positions.

15. Coordinate systems: Cartesian
An intersection of 3 planes:
x = const; y = const; z = const
1;
0.
x x y y z z
x y x z y z
x y z
y z x
z x y
u u u u u u
u u u u u u
u u u
u u u
u u u
= = =
= = =
 =

 = 

 = 
Properties:
An arbitrary vector:
x x y y z zA A u A u A u= + +

16. Coordinate systems: Cartesian
A differential line element:
dl = ux dx + uy dy + uz dz
Three of six differential surface
elements:
dsx = ux dydz
dsy = uy dxdz
dsz = uz dxdy
The differential volume element
dv = dxdydz

17. Coordinate systems: Cylindrical
(polar)
An intersection of a
cylinder and 2 planes
z
z
dl d u d u dz u
ds d dz u d dz u d d u
dv d d dz
 
 
  
     
  
= + +
= + +
=
Diff. length:
Diff. area:
Diff. volume:
An arbitrary vector: z zA A u A u A u   = + +

19. Coordinate systems: Spherical
An intersection of a sphere of radius r, a plane that makes an angle  to the x axis, and
a cone that makes an angle  to the z axis.

21. Coordinate systems: Spherical
r
r
r
u u u
u u u
u u u
 
 
 
 =

 = 

 = 
Properties:
2
2
sin
sin sin
sin
r
r
dl dr u r d u r d u
ds r d d u r dr d u r dr d u
dv r dr d d
 
 
  
     
  
= + +
= + +
=
Diff. length:
Diff. area:
Diff. volume:
An arbitrary vector: r rA A u A u A u   = + +

22. 22

23. 23

24. Matlab commands
cart2pol, cart2sph,
pol2cart, sph2cart

25. Maxwell’s equations are the complete laws of classical
electromagnetism.
Maxwell’s Equations
t
B
E


−=
D
H J
t

 = +

D  =
0B =
Maxwell-Faraday’s Equation
(Faraday’s law of induction)
Ampere’s Law with
Maxwell’s correction
Displacement current
density
Gauss’ Law
Gauss’ Law for magnetism
J
t

 = −

Continuity equation
(implicit in Maxwell’s eqn.s)

26. Maxwell’s Equations
t
B
E


−=
D
H J
t

 = +

D  =
0B =
J
t

 = −

Differential Form
C S
E dl B ds
t

 = − 
 
Integral Form
C S S
H dl J ds D ds
t

 =  + 
  
C V
D ds dv = 
0
C
B ds =
C V
J ds dv
t


 = −
 

27. Maxwell’s Equations
Constitutive Relations
D E=
B H=
J E=

28. Time-harmonic Maxwell’s Equations
• If the sources are time-harmonic (sinusoidal), and all media are linear,
then the electromagnetic fields are sinusoids of the same frequency as
the sources.
• In this case, we can express the quantities by their phasor
representations in the frequency-domain for simplicity.

29. Time-harmonic Maxwell’s Equations
E j B = −
H J j D = +
D  =
0B =
J j = −
Differential Form
C S
E dl j B ds = −  
Integral Form
C S S
H dl J ds j D ds =  +   
C V
D ds dv = 
0
C
B ds =
C V
J ds j dv  = − 

30. Plane wavefront
E
H
ˆn
nHE ˆ⊥⊥
E
Hˆn
Plane waves are TEM waves.
(Transverse ElectroMagnetic)
Plane Electromagnetic Waves

31. POLARIZATION

35. Polarization
Polarization is a description of how the direction of the electric field vector changes
with time at a fixed point in space. If the wave is propagating in the positive z-
direction, the electric field vector at a fixed point, say z=0, can be expressed in the
following general form:
Then, the polarization can be categorized using the two real
quantities A and .
( ) ( ) ( ) ++== tAEatEatzE yx cosˆcosˆ,0 00

36. Polarization
If the locus of the tip of the E-field is a straight line, linear polarization.
Circular locus → Circular polarization.
Elliptical locus → Elliptical polarization.
The polarization is called right-handed, if the fingers of the right hand follow the
direction of rotation of the E-vector while the thumb points in the direction of
propagation. Otherwise, left-handed.
Linear Circular Elliptical

37. Power in a wave
• A wave carries power and transmits it wherever it
goes
The power density per
area carried by a wave is
given by the Poynting
vector.

38. Introduction to Antennas
38

39. Antenna: Linkage Between Circuits and Fields
• Steady-state time-varying signals (e.g., RF CW)
• Transient signals (e.g. Electromagnetic pulses)
• Knowledge of basic RF concepts needed.
Circuits Fields
V, I, Z, P E, H,h, S
Antenna
39

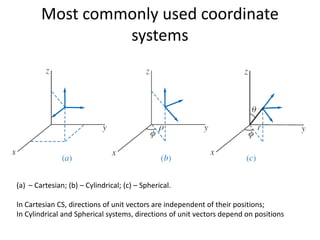
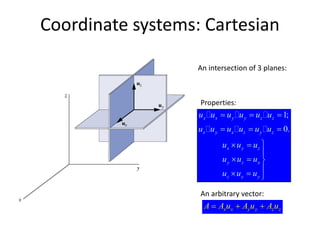
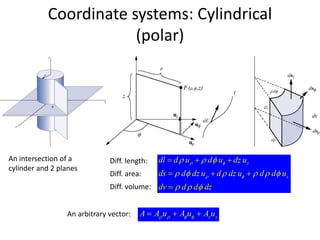
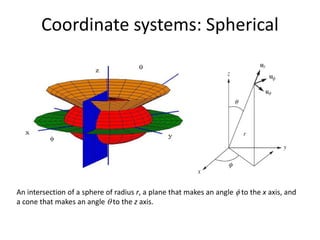
40. Electromagnetic Spectrum
• The Electromagnetic Spectrum covers a very wide range of frequency,
from almost DC to gamma rays.
• Radio frequency (RF) is a subset of the EM spectrum and is loosely
defined as:
“The frequency in the portion of the electromagnetic spectrum that is
between the audio-frequency portion and the infrared portion. The present
practical limits of radio frequency are roughly 10 kHz to 100 GHz.” [IEEE
Std 100-1988 Standard Dictionary of Electrical and Electronic Terms]
• EM (Electromagnetic) waves can propagate in vacuum but not acoustic
waves.
40

41. Frequency – Wavelength Relationship
• The wavelength l of an electromagnetic wave is related to its frequency f
by:
• Conveniently in practice, we can quickly estimate the wavelength of a
frequency given in MHz or GHz by:
f
c
=l where c = 3x108 m/s (speed of light in vacuum)
)m(
fMHz
300
=l
)mm(
fGHz
300
=l
41
e.g., l of 100 MHz is 3 m.
e.g., l of 10 GHz is 30 mm.
41

42. RF Band Names
Band Name Abbr. Frequency Wavelength Examples of Usage
Extremely Low Frequency ELF 3-30 Hz 10-100 Mm
Super Low Frequency SLF 30-300 Hz 1-10 Mm power lines
Ultra Low Frequency ULF 0.3-3 kHz 0.1-1 Mm
Very Low Frequency VLF 3-30 kHz 10-100 km submarines
Low Frequency LF 30-300 kHz 1-10 km beacons
Medium Frequency MF 0.3-3 MHz 0.1-1 km AM broadcast
High Frequency HF 3-30 MHz 10-100 m short-wave radio
Very High Frequency VHF 30-300 MHz 1-10 m FM and TV broadcast
Ultra High Frequency UHF 0.3-3 GHz 0.1-1 m TV, WiFi, mobile phones, GPS
Super High Frequency SHF 3-30 GHz 10-100 mm radar, satellites, WLAN data
Extremely High Frequency EHF 30-300 GHz 1-10 mm radar, automotive, data
42

43. Microwave Band Names
43
Band Name Frequency
L 1-2 GHz
S 2-4 GHz
C 4-8 GHz
X 8-12 GHz
Ku 12-18 GHz
K 18-26 GHz
Ka 26-40 GHz
U 40-60 GHz
43

44. Frequency/Spectrum Allocation/Management
• RF frequency allocation is controlled by:
– ITU (International Telecommunication Union)
• a United Nations agency
• divides the world into three regions (North/South America,
Europe/Africa, Asia/Australia/NZ)
• divides the spectrum for re-allocation by individual countries
– Country-specific National Bodies, e.g.,
• FCC = Federal Communications Commission (USA)
• ACMA = Australian Communications & Media Authority
<www.acma.gov.au>
44

45. Wireless System Frequencies
• Frequencies are allocated according to types of application (sometimes called
“service”).
• Examples of application include:
• Mobile phones (around 900 MHz and higher bands)
• WLANs (around 900 MHz, 2.4 GHz and 5.8 GHz)
• ISM (Industrial, Medical and Scientific) (same as WLANs plus others)
• Variation in frequency allocation is allowed in different nations.
• Wireless products from one country may not work, or allowed to be used,
in another country.
45

46. what is an antenna ?
(everything can radiate)
- antenna is a filter in frequency
and spatial domain

47. Types of Antennas
• Wire Antennas
– dipoles, monopoles, loops, helix, …
– most common
– personal, automobiles, buildings, ships, aircraft, spacecraft …
• Aperture Antennas
– horns, waveguide opening …
– can be flush-mounted
– aircraft, spacecraft …
• Microstrip Antennas
– metallic patch above a ground plane, e.g. circular, rectangular …
– low profile
– personal, aircraft, spacecraft, satellites, missiles, cars, mobile phones
…
47

48. Types of Antennas (cont'd)
• Array Antennas
– Yagi-Uda, aperture array, microstrip patch array, slotted-waveguide
array …
– controllable radiation pattern
• Reflector Antennas
– parabolic, corner reflector …
– high gain
• Lens Antennas
– convex-plane, convex-convex, convex-concave, concave-plane …
– good for very high frequency applications
– size and weight disadvantages
48

49. Common Antenna Types for Wireless Applications
• Top- and/or bottom-loaded monopole/whip with 1
or 2 steps retractable antennas
• Stub Antennas – usually using a spiral antenna
• PIFA Antennas – easily fabricated on printed-circuit-
board
• Ceramic Patch Antennas
• Ceramic Chip Antennas – physically small
• Divergent Antennas – innovative physically small
antennas
49

50. External vs Integrated Antennas
• External Antenna
– Higher antenna gain
– Longer range
– More space required
– Higher costs
• Integrated Antenna
– Compact
– Low-cost design
– Lower antenna gain
– RF attenuation by box
– Shorter range
50

51. Antenna as an Interface/Transducer
Antennas are conducting or dielectric structures that allow efficient launching or
radiating of electromagnetic waves into space. (Theoretically, any structure can
radiate EM waves but not all structures can do it efficiently.)
An antenna can be viewed as a transducer between a transmission line (or
directly from an electrical or electronic circuit) and the surrounding medium. It
can be used for either transmitting or receiving.
RF Generator
(including
Transmission Line)
EM wave
radiating
into space
Antenna
wave front of EM
wave
51

52. Examples of stationary, retractable/telescopic and embedded/hidden antennas
used in commercial cellular and cordless telephones, walkie-talkies, and CB
radios.

53. Triangular array of dipoles used as a sectoral base-station
antenna for mobile Communication.

54. The Arecibo Observatory Antenna
System
The world’s
largest single
radio telescope
304.8-m
spherical
reflector
National
Astronomy and
Ionosphere
Center (USA),
Arecibo,
Puerto Rico

55. The Arecibo Radio Telescope

56. 56
A satellite dish is a parabolic
reflector antenna

58. Different types of horns

59. Horn_Antenna-
in_Holmdel,_New_Jersey

60. Antenna Arrays

61. Antenna Arrays

62. Antenna Arrays

63. Antenna Arrays

64. Westerbork

65. THANK YOU