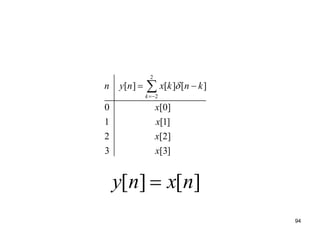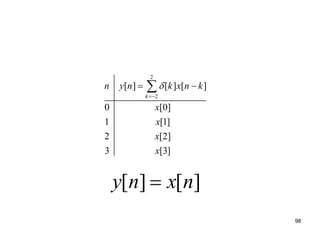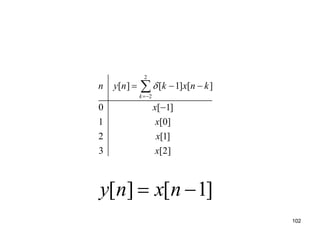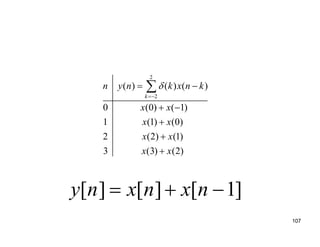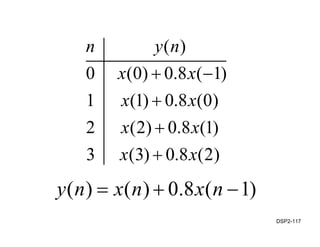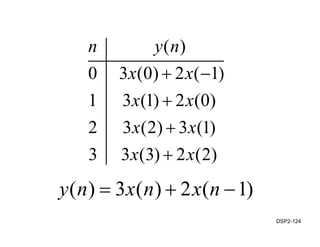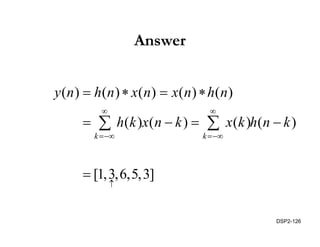Download as PDF, PPTX
Uploaded byPeerapol Yuvapoositanon
PDF, PPTX202 views
DSP 2
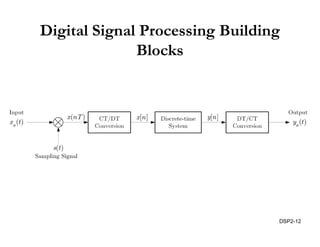
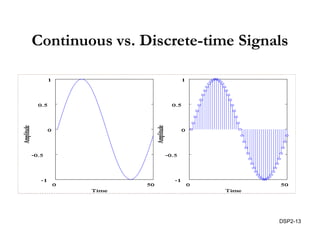
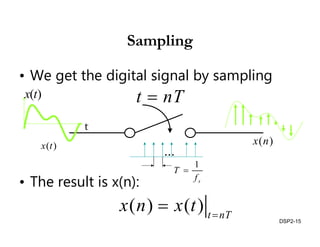
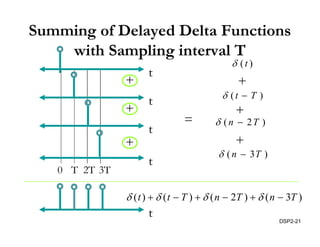
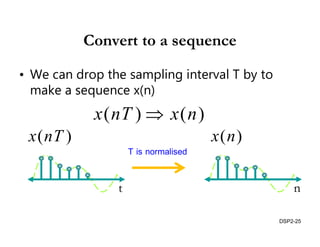
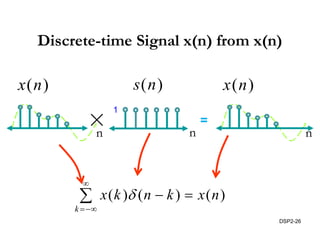
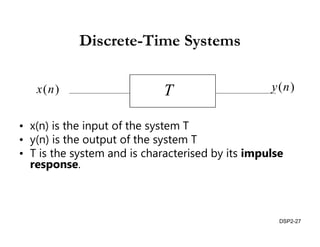
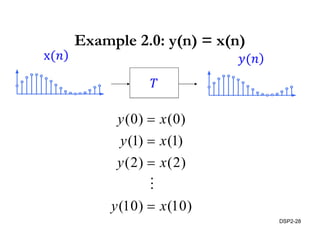
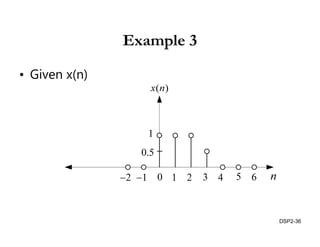
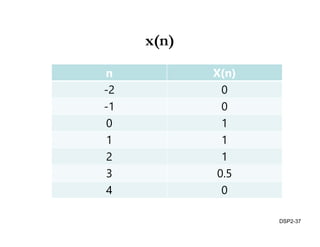
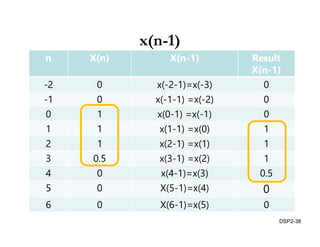
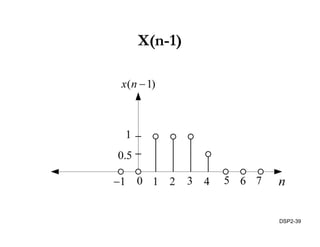
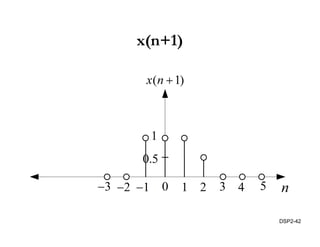
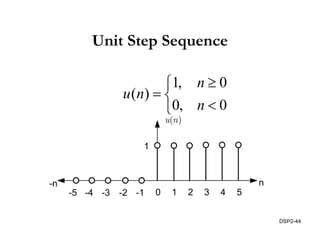
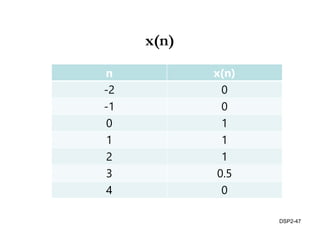
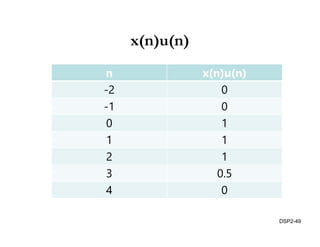
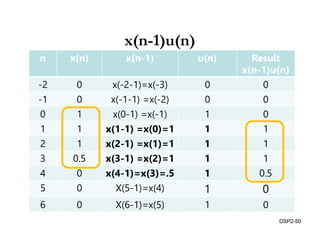
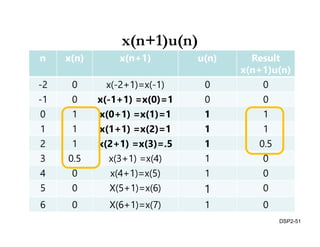
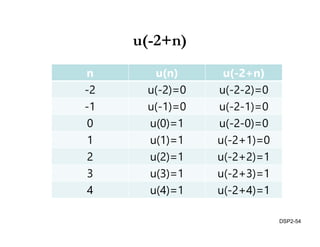
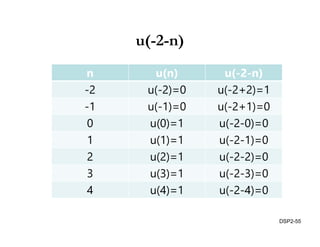
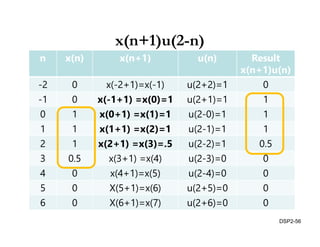
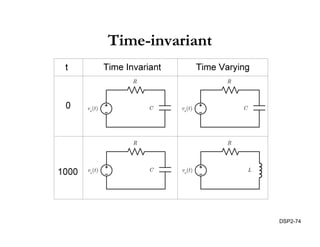
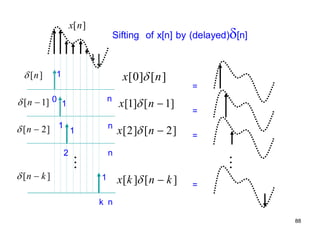
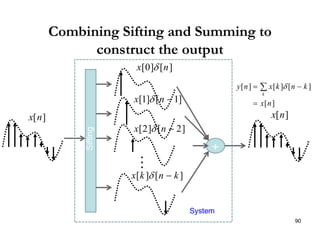
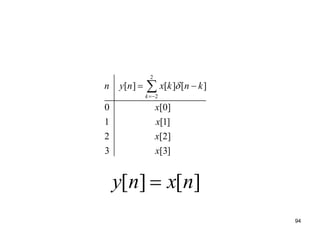
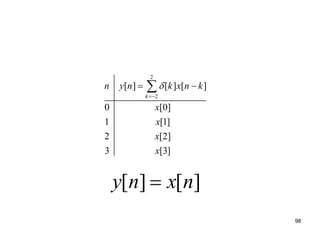
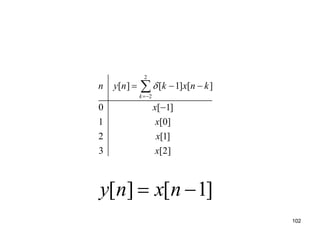
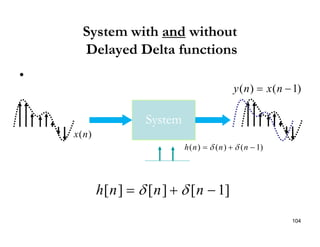
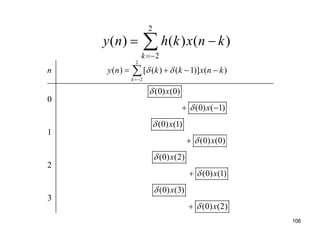
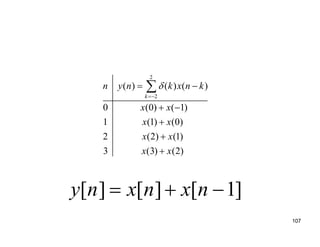
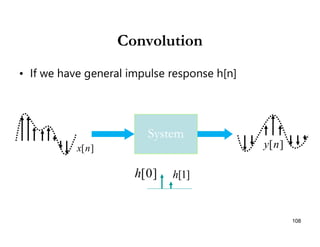
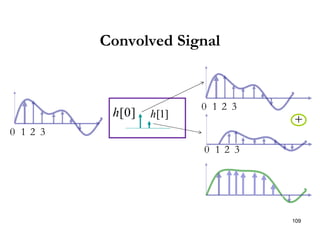
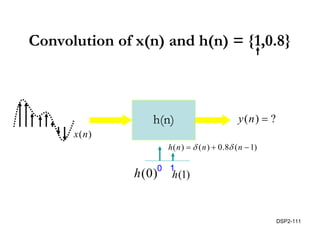
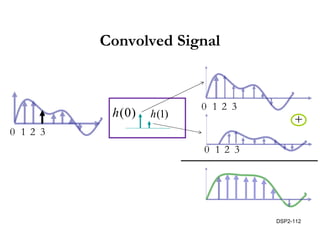
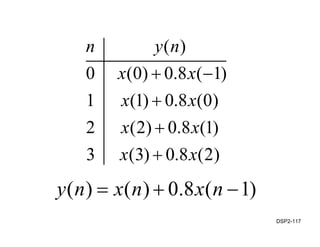
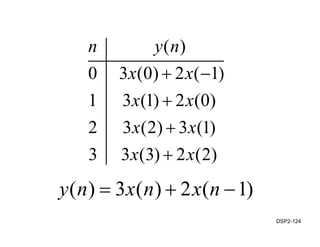
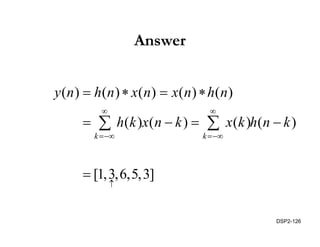
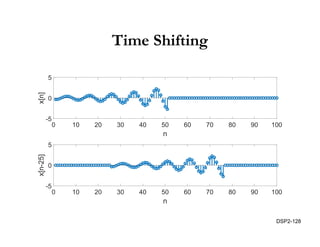
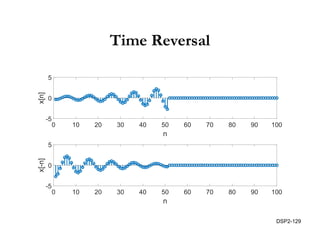
This document discusses discrete-time signals and systems. It defines discrete-time signals as continuous-amplitude signals that are represented by a discrete sequence of values obtained through sampling a continuous-time signal. Linear time-invariant systems are introduced as systems where the output is the input convolved with the system's impulse response. Examples of discrete-time signals and systems are provided to illustrate concepts such as shifting signals by adding or subtracting from the time index n.
Related topics:
![Digital Signal Processing[ECEG-3171]-Ch1_L03](https://cdn.slidesharecdn.com/ss_thumbnails/dspl3-180427094423-thumbnail.jpg?width=640&height=640&fit=bounds)
![Digital Signal Processing[ECEG-3171]-Ch1_L02](https://cdn.slidesharecdn.com/ss_thumbnails/dspl2-180427094423-thumbnail.jpg?width=640&height=640&fit=bounds)
