This document summarizes an article from the journal Energy and Buildings. The article presents a model of a heating, ventilation and air conditioning (HVAC) system that includes both physical and empirical submodels. A pre-cooling coil is added to the HVAC system to help control humidity more efficiently. The hybrid model uses principles of thermodynamics and mass conservation to model different subsystems, while also employing an empirical residential load factor method to account for variations in thermal inertia. The full model is verified using theoretical and numerical methods.

![Author's personal copy
Journal Identification = ENB Article Identification = 3159 Date: July 19, 2011 Time: 7:28 pm
Energy and Buildings 43 (2011) 2043–2054
Contents lists available at ScienceDirect
Energy and Buildings
journal homepage: www.elsevier.com/locate/enbuild
Double cooling coil model for non-linear HVAC system using RLF method
Raad Z. Homoda
, Khairul Salleh Mohamed Saharia,∗
, Haider A.F. Almuribb
, Farrukh Hafiz Nagia
a
Department of Mechanical Engineering, University of Tenaga Nasional, Km 7 Jalan Kajang-Puchong, 43009 Kajang, Malaysia
b
Department of Electrical & Electronic Engineering, The University of Nottingham Malaysia Campus, Jalan Broga, 43500 Semenyih, Selangor Darul Ehsan, Malaysia
a r t i c l e i n f o
Article history:
Received 17 August 2010
Received in revised form 19 March 2011
Accepted 22 March 2011
Keywords:
Building model
HVAC system
RLF method
Energy control
a b s t r a c t
The purpose of heating, ventilating and air conditioning (HVAC) system is to provide and maintain a
comfortable indoor temperature and humidity. The objective of this work is to model building structure,
including equipments of HVAC system. The hybrid HVAC model is built with physical and empirical
functions of thermal inertia quantity. Physical laws are used to build the sub-model for subsystems that
have low thermal inertia while the empirical method is used to build the sub-model for subsystems
with high thermal inertia. The residential load factor (RLF) is modeled by residential heat balance (RHB).
RLF is required to calculate a cooling/heating load depending upon the indoor/outdoor temperature. The
transparency, functionality of indoor/outdoor temperatures and simplicity of RLF makes it suitable for
modeling. Furthermore, the parameters of the model can be calculated differently from room to room and
are appropriate for variable air volume (VAV) factor. Nowadays, a VAV system is universally accepted as
means of achieving both energy efficiency and comfortable building environment. In this research work, a
pre-cooling coil is added to humidify the incoming air, which controls the humidity more efficiently inside
conditioned space. The model presented here is verified with both theoretical and numerical methods.
© 2011 Elsevier B.V. All rights reserved.
1. Introduction
The pioneering simulation work of Stephenson and Mitalas [1]
on the response factor method significantly improved the modeling
of transient heat transfer through the opaque fabric and the heat
transfer between internal surfaces and the room air. The heat bal-
ance approaches were introduced in the 1970s [2] to enable a more
rigorous treatment of building loads. Rather than utilizing weight-
ing factors to characterize the thermal response of the room air due
to solar incident, internal gains, and heat transfer through the fab-
ric, instead, the heat balance methodology solves heat balances for
the room air and at the surfaces of fabric components.
Since its first prototype was developed over two decades ago,
the building model simulation system has been in a constant state
of evolution and renewal. Numerical discretization and simulta-
neous solution techniques were developed as a higher-resolution
alternative to the response factor methods [3]. Essentially, this
approach extends the concept of the heat balance methodology to
all relevant building and plant components. More complex and rig-
orous methods for modeling HVAC systems were introduced in the
1980s. Transient models and more fundamental approaches were
developed [4] as alternatives to the traditional approach which per-
∗ Corresponding author. Tel.: +60 3 89212020.
E-mail addresses: Khairuls@uniten.edu.my (K.S.M. Sahari),
haider.abbas@nottingham.edu.my (H.A.F. Almurib).
formed mass and energy balances on pre-configured templates of
common HVAC systems. The delivery of training and the produc-
tion of learning materials [5] are also receiving increased attention.
Additionally, many validation exercises have been conducted [6]
and test procedures developed [7] to assess, improve, and demon-
strate the integrity of simulation tools.
Up to now, many modeling approaches have been available
and the techniques have become quite mature. However, only
two extreme modeling approaches can be generalized. The first
approach, called physical models, builds up models entirely based
on universal laws, physical laws and principles [8]. The second
approach, called empirical models, constructs models entirely based
on experiments or data [9–11].
This study adopted both methods, by employed energy and
mass conservation law to obtain the overall model of the system.
However, to do that for such a system with various thermal iner-
tia subsystems, care must be given to the heat storage capacity
of the subsystem and its relation to the difference in temperature
(input and output temperatures of control volume) and the differ-
ence in the humidity ratio. If heat storage is a function of these two
properties only, then we can apply physical laws directly. This is
applied to HVAC equipment, usually with low thermal capacitance.
However, if it is related to other factors in addition to those two
properties, the empirical laws must be applied, and this case always
with high thermal inertia subsystem. These methods are applied to
building structures (walls, windows, slab floors, ceiling and roofs)
to calculate heating and cooling loads. There are many methods
0378-7788/$ – see front matter © 2011 Elsevier B.V. All rights reserved.
doi:10.1016/j.enbuild.2011.03.023](https://image.slidesharecdn.com/doublecoolingcoilmodelfornon-linearhvacsystemusingrlfmethodauthorspersonalcopy-170910133959/85/Double-cooling-coil-model-for-non-linear-hvac-system-using-rlf-method-author-s-personal-copy-2-320.jpg)
![Author's personal copy
Journal Identification = ENB Article Identification = 3159 Date: July 19, 2011 Time: 7:28 pm
2044 R.Z. Homod et al. / Energy and Buildings 43 (2011) 2043–2054
Nomenclature
˙E energy, J/s
M mass, kg
˙m mass flow rate, kg/s
T temperature, ◦C
ω humidity ratio, kgw/kgda
˙Q cooling/heating load, W
CF surface cooling factor, W/m2
OFt, OFb, OFr opaque-surface cooling factors
DR cooling daily range, K
PXI peak exterior irradiance, W/m2
SHGC solar heat gain coefficient
Doh depth of overhang, m
Xoh vertical distance from top of fenestration to over-
hang, m
Fcl shade fraction closed (0 to 1)
IDF infiltration driving force, L/(x cm2)
R thermal resistance, ◦C/W
IAC interior shading attenuation coefficient
FFs fenestration solar load factor
Et, Ed, ED peak total, diffuse, and direct irradiance, W/m2
TX transmission of exterior attachment
Fshd fraction of fenestration shaded by overhangs or fins
L site latitude, ◦N
exposure (surface azimuth),◦ from south
SLF shade line factor
used to calculate the heating and cooling load; these methods have
complicated characteristics due to thermal capacitance variation
for different buildings, which affect the heat storage properties.
Since the heat storage properties depend on ambient temperature,
solar gain incident on the building envelops and internal heat-
ing loads [12], and combination of all these elements producing a
time-varying load or time-varying heat flow with such a variation
causing the complication in cooling and heating load calculation
[13].
Therefore, the building and HVAC system structures are includ-
ing both types of high and low thermal inertia, this paper proposes
the hybridization between the two modeling approaches, physical
and empirical, to arrive at an accurate model of the overall system.
The RLF method was derived by [14,15] from residential heat
balance (RHB), where the RLF method is built by applying several
thousand RHB cooling load results, and using these results to create
RLF by statistical regression technique to find values for the load
factors. The procedure method of RLF is presented by ASRAE [16].
There are many reasons to adopt this method to build a model:
it is suitable to be applied on the computer process, it can be used
to calculate a cooling and heating load depending on inside and
outside temperature, cooling and heating loads can be calculated
room by room, and also due to its appropriateness for variable air
volume (VAV) systems. The VAV system is one of two types of mul-
tiple zone heating and ventilation systems. The second type is the
constant air volume (CAV). VAV systems are becoming very popu-
lar in the last few years because of the significant energy savings
they provide as compared to the CAV multiple zone central system.
Furthermore, a VAV scheme can be used to condition occupied part
of a building.
To accommodate humid climates and environments, energy
savings can be achieved by adding a pre-cooling coil. This type of
configuration results in a considerable amount of energy saving and
it is done by reducing reheating process [17].
2. Model development
HVAC systems can be divided into subsystems where each is
modeled separately and then combined to form the overall system
model. There are six attributes of the physical space that influ-
ence comfort: lighting, thermal, air humidity, acoustical, physical,
and the psychosocial environment. Of these, only the thermal con-
ditions and air humidity can be directly controlled by the HVAC
system. Therefore, the construction of building models discussed
in this work is based on these two attributes.
The conditioned space temperature represents the principal
part of a thermal building output. To readily model the behavior
of an overall HVAC system under thermal analysis, theory of con-
servation of energy is applied. This is due to the fact that energy
can enter and exit a subsystem control volume by heat transfer
and flowing streams of matter, which are dominant in any HVAC
process.
Moisture transfer processes are not only caused by internal gen-
eration processes and air migration from outside but also by the
condition of the air being injected into the zone by an air condi-
tioning system. To monitor the variation of moisture in an air flow,
theory on conservation of mass must be applied to the subsystem
control volume. Based on this, for a control volume concept with a
multi-dimensional flow at a multi-inlet and a multi-outlet system,
were applied on HVAC system.
The model of a HVAC system can be represented by a large num-
ber of non-linear, partial differential equations. Most of which are
related to moisture flow and heat transfer involving partial deriva-
tives of time and space. Solution of a set of these equations is very
difficult and therefore, some simplifying assumptions have to be
made [18]. For analysis purposes, the HVAC system is divided into
a number of sections, and for each lumped parameter section, the
humidity ratio and the air temperature are assumed to vary only in
the axial directions and linearly with space. Linearizing the partial
differential equations reduces these equations to ordinary linear
differential equations by applying small perturbation and lumped
parameter techniques. In this work, the linearization process is
based on the following assumptions:
• The air temperature after heat exchanger is almost equal to the
surface temperature of the heat exchanger and Th,t ≈ Tos,t as advo-
cated by Wang et al. [19].
• The conditioned space temperature is homogenous (lumped).
• No dead time exists between subsystem, i.e. the input of a sub-
system is the output of the previous one without any delay.
• The quantities of thermal inertia are already linearized by the RLF
method.
The proposed model is developed to determine the optimal
response for the indoor temperature and humidity ratio by using
temperature and moisture transmission based on the hybridiza-
tion of physical and empirical methods. The main advantage of this
hybrid model approach is its ability to generate the relationship
between indoor and outdoor variation data like a temperature and
humidity ratio. This approach combines both low and high thermal
inertia to get the overall system model.
Since a large number of variables are required to describe the
mathematical model of the HVAC system, it is necessary to devise
a systematic convention for naming the variables. Due to this, the
HVAC components are divided into five subsystems. Fig. 1 shows a
model scheme based on the following subsystems control volume:
• Pre-cooling coil
• Mixing air chamber
• Main cooling coil](https://image.slidesharecdn.com/doublecoolingcoilmodelfornon-linearhvacsystemusingrlfmethodauthorspersonalcopy-170910133959/85/Double-cooling-coil-model-for-non-linear-hvac-system-using-rlf-method-author-s-personal-copy-3-320.jpg)
![Author's personal copy
Journal Identification = ENB Article Identification = 3159 Date: July 19, 2011 Time: 7:28 pm
R.Z. Homod et al. / Energy and Buildings 43 (2011) 2043–2054 2045
Fig. 1. Representation of subsystem using control volume concept for prototypical buildings with HVAC system.
• Building structure
◦ Opaque surfaces structure
◦ Transparent fenestration surfaces structure
◦ Slab floor structure
• Conditioned space
The following subsections describe the modeling of each of the
above subsystems.
2.1. Pre-cooling coil
The conservation of energy is applied to the control volume of
pre-cooling coil as shown in Fig. 2, and the first law of thermody-
namics can be expressed as follows:
energy accumulation in the metal mass of coil
MHecpHe
dTh,t
dt
=
energy absorbed by the coil
˙mw,tcpw(Two − Twin)
+
sensible energy delivered by air
˙mo,tcpa(To,t − Tos,t) +
latent energy delivered by air dehumidification
˙mo,t(ωo,t − ωos,t)hf g (1)
where MHe is the mass of heat exchanger (kg), cpHe is the specific
heat of heat exchanger (J/(kg ◦C)), ˙mw,t is the mass flow rate of
chilled water at time t (kg/s), Th,t, Tos,t, To,t are the temperature of
heat exchanger, out supply air and out air, respectively, at time t
(◦C), Two, Twin are the water out/in heat exchanger temperature (◦C),
˙mo,t is the mass flow rate of outside air at time t (kg/s).
On the other hand, the variation of humidity ratio in control
volume for pre-cooling coil is calculated by applying mass conser-
Fig. 2. Thermal and moisture variation through pre-heat exchanger.
vation on air flow stream. The following can be obtained:
latent energy delivered by air dehumidification
˙mo,t(ωo,t − ωos,t)hfg =
energy absorbed by the coil
˙mw,tcpw(Two − Twin)
−
sensible energy delivered by air
˙mo,tcpa(To,t − Tos,t) (2)
Following the procedure presented by Ghiaus et al. [20], the
state space equations can be obtained. The dynamic subsystem
model of the pre-cooling coil is therefore:
˙x = Aprex + Bpreupre
ypre = Cprex + Dpreupre
(3)
where
x = [ Tos,t ωos,t ]
T
, upre = [ ˙mW To ωo ]
T
,
Apre =
⎡
⎢
⎣
−
˙mo,tcpa
MHecpHe
−
˙mo,thf g
MHecpHe
−
˙mo,tcpa
Mahecpfg
−
˙mo,t
Mahe
⎤
⎥
⎦,
Bpre =
⎡
⎢
⎣
−
cpw tw
MHecpHe
˙mo,tcpa
MHecpHe
˙mo,thf g
MHecpHe
−
cpw tw
Mahehf g
˙mo,tcpa
Mahehf g
˙mo,t
Mahe
⎤
⎥
⎦,
Cpre = [ 1 1 ], Dpre = 0
where Mahe is the mass of air in heat exchanger (kg), Tos,t and ωos,t
are the temperature and humidity ratio of out air supplied, respec-
tively.
A complete description of the physical behavior for the two main
output components (temperature and humidity ratio of out air sup-
plied) are obtained by taking the Laplace transformation of both
sides of Eq. (3), assuming zero initial condition to get:
Tos(s)
ωos(s)
=
G1,1 G1,2 G1,3
G2,1 G2,2 G2,3
˙mw(s)
To(s)
ωo(s)
(4)
where G1,1 = −cpw tw 2S/cpa ˙mo(( 1s − 1)( 2S + 1) + 1), G1,2 =
2S/(( 1s − 1)( 2S + 1) − 1), G1,3 = hfg 2S/cpa(( 1s − 1)( 2S + 1) − 1),
G2,1 = −cpw tw 2s/hfg ˙mo(( 2S + 1)( 1s − 1) + 1), G2,2 = cpa 1s/hfg
(( 2S + 1)( 1s − 1) − 1), G2,3 = 1s/(( 2S + 1)( 1s − 1) − 1), 1 =
MHecpHe/ ˙mocpa (time constant, s), 2 = Mahe/ ˙mo.
2.2. Mixing air chamber
To formulate an overall energy balance for this subsystem, the
energy is transferred within the controlled volume at a uniform rate](https://image.slidesharecdn.com/doublecoolingcoilmodelfornon-linearhvacsystemusingrlfmethodauthorspersonalcopy-170910133959/85/Double-cooling-coil-model-for-non-linear-hvac-system-using-rlf-method-author-s-personal-copy-4-320.jpg)
![Author's personal copy
Journal Identification = ENB Article Identification = 3159 Date: July 19, 2011 Time: 7:28 pm
2046 R.Z. Homod et al. / Energy and Buildings 43 (2011) 2043–2054
Fig. 3. Thermal and moisture variation through air mixing chamber.
by streams of air as shown in Fig. 3. The time dependent thermal
balance equation can be expressed as follows:
energy accumulation in air mass of mix chamber
Mmcpa
dTm,t
dt
= −
energy leaving by air out
˙mm,tcpaTm,t
+
energy delivered by air in
˙mos,tcpaTos,t + ˙mr,tcpaTr,t (5)
where Mm is the mass of air in control volume of mixing air chamber
(kg), cpa is the specific heat of moist air (J/(kg ◦C)), Tm,t, Tos,t, Tr,t is
the Mixing, outside supply and return temperature, respectively,
at time t (◦C), ˙mos,t, ˙mr,t, ˙mm,t is the mass flow rate of ventilation,
return and mixing air at time t (kg/s), Mmcpa is the heat capacitance
of air for mixing air chamber (J/◦C).
The effectiveness of the humidity ratio can be similarly modeled
to the thermal model by applying the principle of mass conserva-
tion to a control volume of mixing box, which can be expressed
as:
mass accumulation in mixing air chamber
dMmωm
dt
=
mass delivered by air in
˙mosωos,t + ˙mrωr,t
−
mass leaving by air out
( ˙mr + ˙mos)ωm,t (6)
where Mm is the mass of air in the mixing chamber (kg), ωr, ωos,
and ωm are humidity ratio of return, outdoor supply and mixing,
respectively (kgw/kgair).
The state space dynamic model of subsystem can be defined as
˙x = Amxx + Bmxumx
ymx = Cmxx + Dmxumx
(7)
where
x = [ Tm,t ωm,t ]
T
, umx[ Tos ωos ˙mos ˙mr ]
T
,
Amx =
−1 0
0 −
˙mr
Mm
, Bmx =
⎡
⎢
⎣
˙mos,t
2Mm
0
Tos,t
2Mm
Tr,t
0
˙mos
Mm
−
ωm,t
Mm
ωr,t
Mm
⎤
⎥
⎦,
Cmx = [ 1 1 ], Dmx = 0
and ymx = [ Tm,t ωm,t ]
T
is the output of the subsystem, tempera-
ture and humidity ratio of mixing air.
The procedure for obtaining the relation between the input and
the output (eliminating the states vector x) is similar to the pre-
cooling coil by taking the Laplace transformation of both sides of
Eq. (7) to get:
Tm(s)
ωm(s)
=
G1,4 G1,5 G1,6 G1,7
G2,4 G2,5 G2,6 G2,7
⎡
⎢
⎣
Tos(s)
ωos(s)
˙mos(s)
˙mr(s)
⎤
⎥
⎦ (8)
where G1,4 = ˙mos/2 ˙mm( chS + 1), G1,5 = 0, G1,6 = os/2 ˙mm( chS +
1), G1,7 = r/ ˙mm( chS + 1), G2,4 = 0, G2,5 = ˙mos/2 ˙mm( chS + 1),
G2,6 = ωos/2 ˙mm( chS + 1), G2,7 = ωr(s)/ ˙mm( chS + 1), ch =
Mm/ ˙mm (time constant, s).
2.3. Main cooling coil
The method for obtaining the relation between the input and
the output is similar in the pre-cooling coil where we applied con-
servation of both energy and mass on main cooling coil control
volume. Following the same manner for the pre-cooling coil to get
thermal and moisture dynamic subsystem equations, the following
state space can be derived:
˙x = Amx + Bmum
ym = Cmx + Dmum
(9)
where
x = [ Ts,t ωs,t ]
T
, um = [ ˙mmw Tm ωm ]
T
,
Am =
⎡
⎢
⎣
−
˙mm,tcpa
MmHecpHe
−
˙mm,thf g
MmHecpHe
−
˙mm,tcpa
Mmahehf g
−
˙mm,t
mmahe
⎤
⎥
⎦,
Bm =
⎡
⎢
⎣
−
cpw tw
MmHecpHe
˙mm,tcpa
MmHecpHe
˙mm,thf g
MmHecpHe
−
cpw tmw
Mmahehf g
˙mm,tcpa
Mmahehf g
˙mm,t
Mmahe
⎤
⎥
⎦,
Cm = [ 1 1 ], Dm = 0
and ym = [ Ts,t ωs,t ]
T
is the output of the subsystem, temperature
and humidity ratio of supplied air to conditioned space.
To eliminate the states vector x, we follow similar method in the
pre-cooling coil by taking Laplace transformation on both sides of
Eq. (9) to get:
Ts(s)
ωs(s)
=
G1,8 G1,9 G1,10
G2,8 G2,9 G2,10
˙mmw(s)
Tm(s)
ωm(s)
(10)
where G1,8 = −cpw tmw 4S/cpa ˙mm(( 3s − 1)( 4S + 1) + 1), G1,9 =
4S/(( 3s − 1)( 4S + 1) − 1), G1,10 = hfg 4S/cpa(( 3s − 1)( 4S + 1) − 1),
G2,8 = −cpw tmw 3s/hfg ˙mm(( 4S + 1)( 3s − 1) + 1), G2,9 =
cpa 3s/hfg(( 4S + 1)( 3s − 1) − 1), G2,10 = 3s/(( 4S + 1)( 3s − 1) − 1),
3 = MmHecpHe/ ˙mmcpa (time constant, s), 4 = Mmahe/ ˙mm (time
constant, s), MmHe is the mass of main heat exchanger (kg), cpHe is
the specific heat of heat exchanger (J/(kg ◦C)), ˙mmw,t is the mass
flow rate of main cooling coil chilled water at time t (kg/s), Th,t, Ts,t,
Tm,t are the heat exchanger, supply air and mixing air temperature,
respectively, at time t (◦C), Two, Twin are the water out/in heat
exchanger temperature (◦C), (Two − Twin) = tmw cooling design
temperature difference (◦C).
Most cooling coil models can be utilized only when the coil is
totally dry or totally wet because they are based on the convection
heat transfer coefficient, which is dependent on the nature of the
surface, e.g. Ghiaus et al. [20] and Wang et al. [21] models. On the
other hand, the cooling coil model of this paper is developed based
on the application of mass and energy conservation Balance rules
on the control volume basis. This method is not affected by the
nature of the surface.
2.4. Building structure
The thermal mass of the building structure creates a load lev-
eling or flywheel effect on the instantaneous load. There are three](https://image.slidesharecdn.com/doublecoolingcoilmodelfornon-linearhvacsystemusingrlfmethodauthorspersonalcopy-170910133959/85/Double-cooling-coil-model-for-non-linear-hvac-system-using-rlf-method-author-s-personal-copy-5-320.jpg)
![Author's personal copy
Journal Identification = ENB Article Identification = 3159 Date: July 19, 2011 Time: 7:28 pm
R.Z. Homod et al. / Energy and Buildings 43 (2011) 2043–2054 2047
Fig. 4. Heat transfer by face temperature difference.
factors associated with the heat gain/losses to/from building struc-
ture as a result of outdoor temperature and solar radiation. These
factors are related to opaque surfaces (walls, ceilings, roofs and
doors), transparent fenestration surfaces (windows, skylights and
glazed doors) and slab floors. To create building model structure
with ambiguity of thermal flywheel effectiveness on indoor tem-
perature, we used empirical RLF method.
2.4.1. Opaque surfaces
Heat transfer in opaque surfaces is due to conduction, convec-
tion and radiation. During which a stored heat will fluctuate with
time. This is mainly due to two factors: the dramatic change of tem-
perature outside the system, and solar radiation that also change
dramatically during the day. To calculate this thermal capacitance,
we apply the energy conservation law of Eq. (11) on the system’s
control volume. The left hand side of the equation represents the
accumulate rate of thermal storage of opaque surfaces while the
right hand side corresponds to the heat that enters and goes out
through the control volume [22,23]:
accumulation of energy
Mwlcpwl
dTwl,t
dt
=
difference between in and out of energy
i
˙Qopqin
−
i
˙Qopqout (11)
where, Mwlcpwl is the heat capacitance of walls, ceilings, roofs and
doors (J/K), i
˙Qopqin
and i
˙Qopqout is the heat gains and losses
through walls, ceilings, roofs and doors.
The heat that goes into the control volume (heat gain) of opaque
surfaces such as walls, doors, roofs and ceilings is due to two
aspects: the difference in the inside and outside temperatures of
the surfaces as illustrated in Fig. 4, and the gain of the solar incident
on the surfaces. On the other hand, the heat that goes out the con-
trol volume (heat lose) is due to heat convection to the conditioned
space.
The RLF method is used to calculate heating and cooling loads
based on two factors. One is the area of surface (Awj), and the other
is the surface cooling factor (CFopqj
) [16]. Thus, the heat entering the
surface or control volume ( ˙Qopqin
) can be written mathematically as
follows:
˙Qopqin
=
j
Awj
× CFopqj
(12)
and CFopq is defined as:
CFopq = U(OFt t + OFb + OFrDR) (13)
where U is the construction U-factor, W/(m2 K), t is the cooling
design temperature difference (◦C), OFt, OFb, OFr are the opaque-
surface cooling factors, and DR is the cooling daily range (K).
Hence
˙Qopqin
=
j
Awj
Uj OFt(Twlou
− TWIin
) +
j
Awj
UjOFb
+
j
Awj
UjOFrDR (14)
In Eq. (11), ˙Qopqout is the heat transfer due to convection into con-
ditioned space. Following Newton’s law of cooling for convection
heat transfer, ˙Qout can be written as:
˙Qopqout =
j
Awj
hij
(TWIin
− Tr) (15)
Thus, applying RLF method in the entire building using Eq. (11)
will give us an empirical time dependent heat balance equation as
follows:
Mwlcpwl
Twlout ,t − TWIin,t
t
=
j
Awj
UjOFt(Twlout ,t − TWIin,t) +
j
Awj
UjOFb
+
j
Awj
UjOFrDR −
j
Awj
hij
(TWIin,t − Tr,t) (16)
The implication behind Eq. (16) is that the temperature profiles of
the building opaque envelopes are given by the linear combina-
tion of Twlout ,t and TWIin,t as shown in Fig. 4. For a thin, uniform
construction material, the method gives a good estimation. How-
ever, for a thick, heavy mass material, the equation shows a big
error. One way of modifying Eq. (16) is to introduce more nodes,
for example Twlout ,t, T1,t, t2,t, . . . , Tn,t, TWIin,t for approximating the
temperature profile can be represented as the linear combination
of Twlout ,t, T1,t, t2,t, . . . , Tn,t, TWIin,t. Laplace transformation can be
used and the equation is reduced to a first order time lag corre-
sponding to Twlout ,t and TWIin,t as explained below [24]:
Mwlcpwl
dTWlin,t
dt
=
j
Awj
UjOFt(Twlout ,t − Twlin,t) +
j
Awj
UjOFb
+
j
Awj
UjOFrDR −
j
Awj
hij
(TWlin,t − Tr,t) (17)
Taking Laplace transformation on both sides of Eq. (17) and assum-
ing zero initial conditions and simplifyingexpression,we can obtain
the following transfer function:
TWlin
(s) = [ G1,11 G1,12 G1,13 ]
To(s)
k2
Tr(s)
(18)
where G1,11 = k1/( 5s + 1), G1,12 = 1/( 5s + 1), G1,13 = k3/( 5s + 1),
5 = Mwlcpwl/( j
Awj
UjOFt + j
Awj
hij
), k1 = j
Awj
UjOFt/
( j
Awj
UjOFt + j
Awj
hij
), k2 = ( j
Awj
UjOFb + j
Awj
UjOFrDR)/
( j
Awj
UjOFt + j
Awj
hij
), k3 = j
Awj
hij
/( j
Awj
UjOFt +
j
Awj
hij
), the k parameters are k1 is the function of thermal
resistant and outside temperature, k2 is the function of thermal
resistant and solar radiation incident on the surfaces (◦C) and k3 is
the function of thermal resistant and convection heat transfer.
From Eq. (18) the opaque inside temperature surface (TWlin
(s))
inputs are outdoor temperature (To(s)), thermal resistant and solar
radiation incident (k2) and room temperature (Tr(s)).](https://image.slidesharecdn.com/doublecoolingcoilmodelfornon-linearhvacsystemusingrlfmethodauthorspersonalcopy-170910133959/85/Double-cooling-coil-model-for-non-linear-hvac-system-using-rlf-method-author-s-personal-copy-6-320.jpg)
![Author's personal copy
Journal Identification = ENB Article Identification = 3159 Date: July 19, 2011 Time: 7:28 pm
2048 R.Z. Homod et al. / Energy and Buildings 43 (2011) 2043–2054
Fig. 5. Heat transfer through fenestration and windows.
2.4.2. Transparent fenestration surfaces
Heat transfer in this part is somewhat different than in opaque
surfaces. This is because the heat gain of these surfaces consisted of
two parts: the first one represents heat transferred by conduction,
which is the result of the difference between the inner and outer
temperature, and the second part represents the heat transfer due
to solar radiation which itself consists of a group of factors as illus-
trated in Fig. 5. However, Eq. (11) is still valid here, and we can use
it but by changing the way of calculating the heat entering the con-
trol volume (heat gain). The RLF is implicated the components of
the second part with first one to obtain the heat entering the con-
trol volume. As before, the factors used are the area (Afenj
) and the
surface cooling factor (CFfenj
) to calculate the heat gain as follows:
Qfenin
=
j
Afenj
CFfenj
(19)
where CFfenj
is given by equation CFfen = uNFRC( t − 0.46DR) +
PXI × SHGC × IAC × FFs, ˙Qfen is the fenestration cooling load (W), Afen
is the fenestration area (including frame) (m2), CFfen is the surface
cooling factor (W/m2), uNFRC is the fenestration NFRC heating U-
factor (W/(m2 K)), NFRC is the National Fenestration Rating Council,
t is the cooling design temperature difference (K), DR is the cool-
ing daily range (K), PXI is the peak exterior irradiance, including
shading modifications (W/m2), SHGC is the fenestration rated or
estimated NFRC solar heat gain coefficient, IAC is the interior shad-
ing attenuation coefficient, and FFs is the fenestration solar load
factor.
PXI is calculated as follows:
PXI = TX Et (unshaded fenestration) (20)
PXI = TX [Ed + (1 − Fshd)ED] (shaded fenestration) (21)
where PXI is a peak exterior irradiance (W/m2), Et, Ed, and ED are
peak total, diffuse, and direct irradiance, respectively (W/m2), TX
is a transmission of exterior attachment (insect screen or shade
screen), and Fshd is a fraction of fenestration shaded by permanent
overhangs, fins, or environmental obstacles.
Et, Ed, and ED values are based on two surface conditions, where
for horizontal surfaces:
Et = 952 + 6.49L − 0.166L2
, Ed = min(Et, 170) and
ED = Et − Ed (22)
For vertical surfaces
=
180
(normalized exposure, 0–1)
Et = 453.4 + 1341 − 5279 3 + 3260 4 − 34.09 L
+ 0.2643 L2 − 12.83L − 0.8425L2 +
0.9835L2
+ 1
,
Ed = min Et, 357 − 86.98 2 + 1.76 L −
108.4
4
√
L
+ 1
and
ED = Et − Ed
(23)
where L = site latitude, ◦N, = exposure (surface azimuth)◦ from
south (−180 to +180).
The shaded fraction Fshd can be taken as 1 for any fenestration
shaded by adjacent structures during peak hours. Simple overhang
shading is given by an estimated equation:
Fshd = min 1, max 0,
SLF × Doh − Xoh
h
(24)
where SLF is the shade line factor, Doh is the depth of overhang (from
plane of fenestration) (m), Xoh is the vertical distance from top of
fenestration to overhang (m), and h is the height of fenestration
(m).
IAC values are computed as follows:
IAC = 1 + Fcl(IACcl − 1) (25)
where IAC is the interior attenuation coefficient of fenestration
with partially closed shade, Fcl is the shade fraction closed (0 to
1), and IACcl is the interior attenuation coefficient of fully closed
configuration.
Thus, the heat gain through a fenestration is given as:
˙Qfenin
=
j
Afenj
uNFRCj
(To − Tgin
) −
j
Afenj
uNFRCj
× 0.46DR
+
j
Afenj
PXIj × SHGCj × IACj × FFsj
(26)
After obtaining the heat transferred into control volume (heat gain)
of the fenestration surfaces, the same method used in the opaque
surfaces can be followed to get the transfer function. Here, the
inputs are: the outdoor temperature (To), the indoor temperature
(Tr) and the location of the conditioned place (fDR). The output is
the inside temperature of the glass (Tgin
) which is defined as:
Tgin
(S) = [ G1,14 G1,15 F1,16 ]
To(s)
Tr(s)
fDR
(27)
where G1,14 = Rgf1/(f1Rg + 1)( gS + 1), G1,15 = 1/(f1Rg + 1)( gs +
1), G1,16 = −Rg/(f1Rg + 1)( gS + 1), g = Cag Rg/(f1Rg + 1), Rg =
(1/ j
Afenj
hij
), fDR = j
Afenj
uNFRCj
× 0.46D, f1 = j
Afenj
uNFRCj
(W/k).
2.4.3. Slab floors
The slab floor of the building has big thermal capacitance stor-
age. In fact, it is the largest among the different sections of the
building and to calculate it. We can rewrite the energy conservation
law of Eq. (11) as follows:
accumulation or storage of energy
Mslabcpslab
dTslab,t
dt
=
difference between in and out of energy
i
˙Qslabin
−
i
˙Qslabout
(28)](https://image.slidesharecdn.com/doublecoolingcoilmodelfornon-linearhvacsystemusingrlfmethodauthorspersonalcopy-170910133959/85/Double-cooling-coil-model-for-non-linear-hvac-system-using-rlf-method-author-s-personal-copy-7-320.jpg)
![Author's personal copy
Journal Identification = ENB Article Identification = 3159 Date: July 19, 2011 Time: 7:28 pm
R.Z. Homod et al. / Energy and Buildings 43 (2011) 2043–2054 2049
where i
˙Qslabin
and i
˙Qslabout
are the heat gain and loss through
slab floor, respectively (W) and Mwlcpwl is the heat capacitance of
slab (J/K).
Wang [25] and Bligh et al. [26] found that heat gain to concrete
slab floor is mostly through the perimeter rather than through the
floor and into the ground. Total heat loss/gain is more nearly pro-
portional to the length of the perimeter than to the area of the floor,
and it can be estimated by the following equation for both unheated
and heated slab floors:
˙Qslabin
= ft P(Tslabin
− To) (29)
where ˙Qslabout
is the heat loss through slab floors (W), ft is the heat
loss coefficient per meter of perimeter, W/(m K), P is the perimeter
or exposed edge of floor (m), Tslabin
is the inside slab floor tempera-
ture or indoor temperature (◦C), and To is the outdoor temperature
(◦C).
The output heat (heat loss) from concrete slab floor has been
calculated by ASHREA organization by following the same meth-
ods used in the opaque and fenestration surfaces [16]. As before all
factors affecting the output heat have been embedded in two fac-
tors only: the area (Aslabj
) and the cooling surface factors (Cfslabj
).
Therefore, the heat output of control volume is as in Eq. (30):
˙Qslabout
=
j
Aslabj
× Cfslabj
(30)
where Aslab is the area of slab (m2), (Cfslab = 1.9 − 1.4hsrf) is the slab
cooling factor (W/m2), hsrf is given by hsrf = 1/(Rcvr + 0.12), where
hsrf is the effective surface conductance, including resistance of slab
covering material (Rcvr) such as carpet (Representative (Rcvr) val-
ues are found in Chapter 6 of the 2008 ASHRAE Handbook—HVAC
Systems and Equipment [27]).
To obtain slab floor transfer function, Eqs. (29) and (30) are sub-
stituted into Eq. (28), and after simplifying the expression, Laplace
transformation is applied on both sides of the resulting equation.
The slab floors subsystem inputs are slab floors area (Aslab) and
outdoor temperature To, while output is inside slab floors temper-
ature Tslabin
(S) as shown below:
Tslabin
(s) = [ G1,17 G1,18 ]
Aslab
To
(31)
where G1,17 = (1.9 − 1.4hsrf)/( slabS + 1), G1,18 = ftP/( slabS + 1),
slab = Cslab/ftP, Cslab = i
Mslabi
cpslabi
, is the heat capacitance of
slab floors (J/k).
2.5. Conditioned space
The conditioned space is covered by walls, windows, doors,
ceilings, roofs and slab floors. In other words conditioned space
components are air space, furniture, occupant, lighting and appara-
tus that emits heating load. By means of conditioned space control
volume, we analyze the effectiveness of temperature and humid-
ity ratio by applying conservation of energy and mass. The RLF and
physical law are used as analytical tools to model indoor tempera-
ture and humidity ratio.
Sensible heat gain can be evaluated by applying thermal balance
equation on conditioned space to get the components’ thermal load.
The most critical components affecting the conditioned space are:
(1) Heat traversing opaque surfaces ( ˙Qopq), which is the amount
of heat transferred to indoor air from walls, roofs, ceilings and
doors, (2) the heat traversing transparent fenestration surfaces
( ˙Qfen) as in windows, skylights, and glazed doors, (3) through slab
floors ( ˙Qslab), (4) infiltration and ventilation ( ˙Qinf ), (5) occupants,
lighting, and appliance ( ˙Qig,s), (6) furnishing and air conditioning
space capacitance ( ˙Qair + ˙Qfur) and (7) cooling load exerted by HVAC
system ( ˙Qs).
The heat balance of conditioned space is given by the equation:
accumulation or storage of energy
˙Qair + ˙Qfur =
difference between input and output of energy
˙Qopq + ˙Qfen + ˙Qslab + ˙Qinf + ˙Qig,s − ˙Qs
(32)
where
˙Qair =
storage energy at air mass
Maircpa
dTair
dt
,
˙Qfur =
storage energy at furniture mass
j
Mfurj
cpfurj
dTfur
dt
,
˙Qopq =
convection heat gain from opaque surface
j
Awj
hij
(TWlin−Tr
) ,
˙Qfen =
conduction heat gain
(Tgin
− Tr)
Rg
+
solar radiation heat gain
j
Afenj
PXIj × SHGCj × IACj × FFsj
,
˙Qslab =
convention heat gain from slab floors
j
Aslbj
hij
(Tslbin
− Tr) ,
˙Qinf =
heat gain due to infiltration
Cs × AL × IDF(To,t − Tr,t), and
˙Qig,s =
sensible cooling load from internal gains
136 + 2.2Acf + 22Noc .
Substitution these quantities into Eq. (32), yields
Mrcpa
dTr,t
dt
+
j
Mfurj
cpfurj
dTfur,t
dt
=
j
Awj
hij
(TWlin,t − Tr,t) +
gin,t − Tr,t
Rg
+
j
Afenj
PXIj × SHGCj × IACj × FFsj
+
j
Aslbj
hij
(Tslbin
− Tr) + Cs × AL × IAF(To,t − Tr,t)
+ 136 + 2.2Acf + 22Noc − ˙mmcpa(Tr,t − Ts,t) (33)
The rate of moisture change in conditioned space is the result
of three predominant moisture sources: outdoor air (infiltration
and ventilation), occupants, and miscellaneous sources, such as
cooking, laundry, and bathing as shown in Fig. 6. We applied the
conservation of mass law on the components of conditioned space](https://image.slidesharecdn.com/doublecoolingcoilmodelfornon-linearhvacsystemusingrlfmethodauthorspersonalcopy-170910133959/85/Double-cooling-coil-model-for-non-linear-hvac-system-using-rlf-method-author-s-personal-copy-8-320.jpg)
![Author's personal copy
Journal Identification = ENB Article Identification = 3159 Date: July 19, 2011 Time: 7:28 pm
2050 R.Z. Homod et al. / Energy and Buildings 43 (2011) 2043–2054
Fig. 6. Heat and humidity flow in/out of conditioned space.
to get a general formula as follows:
rate of moisture change
= rate of moisture transfer + rate of moisture generation
d moisture value
dt
=
i
input moisture rate
−
e
output moisture rate +
gen
moisture generation rate
(34)
The mass balance of conditioned space is given by the equation:
dMrωr,t
dt
= ˙msωs,t + ˙minf ωa,t +
˙Qig,l
hfg
− ˙mrωr,t (35)
A complete description of the space physical behavior for the
two main output components is given by combining thermal model
equation (33) with moisture model equation (35) deriving the
whole subsystem state space equation of conditioned space as pre-
sented by Ghiaus et al. [28]. Then eliminating the states vector x,
we follow similar method in the pre-cooling coil by taking Laplace
transformation on both sides of the state space equation to get:
Tr(s)
ωr(s)
=
G1,19 G1,20 G1,21 G1,22 G1,23 G1,24 G1,25 G1,26 G1,27
G2,19 G2,20 G2,21 G2,22 G2,23 G2,24 G2,25 G2,26 G2,27
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
TWlin
(s)
Tgin
(s)
Tslbin
(s)
To(s)
Ts(s)
f4
ωs(s)
ωo(s)
˙Qig,l
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(36)
where G1,19 = kwl/f2( 6S + 1), G1,20 = 1/f2Rg( 6S + 1),
G1,21 = kslb/f2( 6S + 1), G1,22 = f3/f2( 6S + 1), G1,23 = ˙mmcpa/f2( 6S +
1), G1,24 = 1/f2( 6S + 1), G1,25 = 0, G1,26 = 0, G1,27 = 0, G2,19 = 0, G2,20 = 0,
G2,21 = 0, G2,23 = 0, G2,24 = 0, G2,25 = ˙ms/ ˙mr( rS + 1), G2,26 =
˙minf / ˙mr( rS + 1), G2,27 = 1/hfg ˙mr( rS + 1), kwl = j
Aslbjhij
,
f3 = Cs × AL × IDF (W/k), Cs is the air sensible heat factor (w/L . S . K.),
AL is the building effective leakage area, cm2, IDF is the infiltration
driving force (L/(s cm2)), f2 = j
Awj
hij
+ (1/Rg) + j
Aslbj
hij
+
Cs × AL × IDF + ˙mmcpa (W/k), 6 = Caf/f2 (s), Caf is the heat
capacitance of indoor air and furniture, ˙minf is the infiltra-
tion air mass flow rate (kg/s), f4 = ffen + 136 + 2.2Acf + 22Noc (W),
ffen = j
Afenj
PXIj × SHGCj × IACj × FFsj
is the direct radiation (W),
ωs, ωo is the humidity ratio of outdoor and supply air, respectively,
and ˙Qig,l is the latent cooling load from internal gains.
3. Resulting overall model
The model block diagram represents a good overall picture of
the relationships among transfer function variables of a subsystem
model. It is possible to arrange the final subsystem’s transfer func-
tions (Eqs. (4), (8), (10), (18), (27), (31) and (36)) in a way to reflect
reality where the output of the first subsystem is the input to the
next subsystem and so on and so forth. This is illustrated by Fig. 7.
Note here that it is difficult to arrange and derive the overall math-
ematical model that represents the system’s general equation by
only looking at these equations. Therefore, we sought the help of
graphics.
A complete description of the plant behavior for the two main
output components is given by compacting subsystem model equa-
tion of pre-cooling coil, mixing air chamber, mean cooling coil,
conditioned space and building structure. The whole compact
model transfer function of HVAC equipment and building is rep-
resented by Eq. (37).
Tr(s)
ωr(s)
=
T1,1(s) T1,2(s) T1,3(s) T1,4(s) T1,5(s) T1,6(s) T1,7(s) T1,8(s) T1,9(s) T1,10(s) T1,11(s) T1,12(s)
T2,1(s) T2,2(s) T2,3(s) T2,4(s) T2,5(s) T2,6(s) T2,7(s) T2,8(s) T2,9(s) T2,10(s) T2,11(s) T2,12(s)
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
˙mw(s)
˙mmw(s)
˙mos(s)
˙mr(s)
To(s)
ωo(s)
f4
˙Qig,l
Aslab
fDR
k2
Tr(s)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(37)
where
T1,1(s), T1,2(s), . . ., T1,12(s) and T2,1(s), T2,2(s), . . ., T2,12(s) represent
the input factors that can be obtained from Eq. (36) and Fig. 7.
Eq. (37) implies that the system has twelve input variables and
two outputs.](https://image.slidesharecdn.com/doublecoolingcoilmodelfornon-linearhvacsystemusingrlfmethodauthorspersonalcopy-170910133959/85/Double-cooling-coil-model-for-non-linear-hvac-system-using-rlf-method-author-s-personal-copy-9-320.jpg)
![Author's personal copy
Journal Identification = ENB Article Identification = 3159 Date: July 19, 2011 Time: 7:28 pm
R.Z. Homod et al. / Energy and Buildings 43 (2011) 2043–2054 2051
Fig. 7. Subsystems model block diagram.
The input variables are:
1. ˙mw(s) is the flow rate of chilled water supply to pre-cooling coil,
2. ˙mmw(s) is the flow rate of chilled water supply to main cooling
coil,
3. ˙mr(s) is the flow rate of return air to conditioned space,
4. ˙mos(s) is the flow rate of outside air to conditioned space,
5. To(s) is the perturbations in outside temperature,
6. k2 is the perturbations due to thermal resistance of building
envelope,
7. f4 is the perturbations of internal sensible heat gain,
8. Aslab is the area of slab floors,
9. fDR is the location factor,
10. ωo (s) is the perturbations in outside air humidity ratio,
11. ˙Qig,l is the perturbations of internal latent heat gain, and
12. Tr(s) is the conditioned space temperature.
On the other hand, the output variables are:
1. Tr(s) is the room temperature or conditioned space temperature,
and
2. ωr(s) is the room humidity ratio or conditioned space humidity
ratio.
4. Simulation results and discussion
In order to evaluate the performance of the previous thermal
moisture model strategies presented in this work, a residential
building used by the RLF methodology [16] has been adopted. The
geometry of the building is shown in Fig. 8 and is the same one
used in ASHRAE [16] to investigate the parameters of the developed
model.
Fig. 8. The geometry of the building chosen to get model parameters.
The building construction characteristics are documented in
Table 1.
The residential building model is a typical one-story house that
has a simple structure. The overall area is 248.6 m2 while the over-
all area excluding the garage is 195.3 m2, the gross windows and
wall exposed area is 126.2 m2 while the net wall exterior area is
108.5 m2, and the overall house volume excluding the garage is
468.7 m3. Other construction characteristics are documented in
Table 1. In order to test the model identification procedure, the
multi-zone model of the RLF methodology has been adopted.
The building properties and weather data obtained for Kuala
Lumpur city have been used for cooling load calculation. By means
of natural ventilation (the HVAC components are turned off)
applied on a building model, then the outside condition and inter-
nal gains are the only affected on the indoor condition. Based on
these conditions, all cooling loads for residential building were cal-
Table 1
Material properties of model building construction.
Component Description Factors
Roof/ceiling Flat wood frame ceiling (insulated with R-5.3 fiberglass)
beneath vented attic with medium asphalt shingle roof
U = 0.03118 W/(m2
K)
˛roof = 0.85
Exterior walls Wood frame, exterior wood sheathing, interior gypsum board,
R-2.3 fiberglass insulation
U = 51 W/(m2
K)
Doors Wood, solid core U = 2.3 W/(m2
K)
Floor Slab on grade with heavy carpet over rubber pad; R-0.9 edge
insulation to 1 m below grade
Rcvr = 0.21 (m2
K)/W; Fp = 85 W/(m2
K)
Windows Clear double-pane glass in wood frames. Half fixed, half
operable with insect screens (except living room picture
window, which is fixed). 0.6 m eave overhang on east and west
with eave edge at same height as top of glazing for all
windows. Allow for typical interior shading, half closed.
Fixed: U = 2.84 W/(m2
K); SHGC = 0.67
Operable: U = 2.87 W/(m2
K); SHGC = 0.57;
Tx = 0.64
IACcl = 0.6
Construction Good Aul = 1.4 cm2
/m2](https://image.slidesharecdn.com/doublecoolingcoilmodelfornon-linearhvacsystemusingrlfmethodauthorspersonalcopy-170910133959/85/Double-cooling-coil-model-for-non-linear-hvac-system-using-rlf-method-author-s-personal-copy-10-320.jpg)
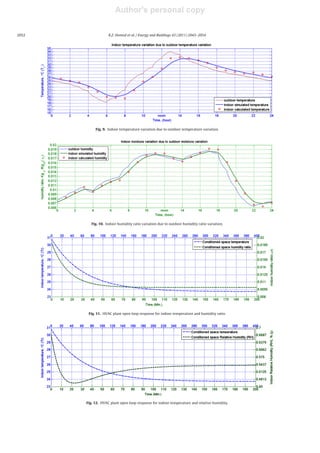
![Author's personal copy
Journal Identification = ENB Article Identification = 3159 Date: July 19, 2011 Time: 7:28 pm
R.Z. Homod et al. / Energy and Buildings 43 (2011) 2043–2054 2053
Fig. 13. Indoor thermodynamic properties transient response for whole building and HVAC plant.
culated every 1 h for 24 h by using numerical methods [29]. These
calculated cooling loads were used to find out the indoor temper-
ature and humidity ratio. And these temperature and humidity
ratio checked against the simulation model outputs as shown in
Figs. 9 and 10. From the figures, we find that there is substantial con-
vergence between the calculated results and the simulation model
outputs.
The effect of HVAC plant on the indoor air temperature and
humidity can be investigated by an open loop response.
4.1. Open loop response
To incorporate the HVAC plant in the simulation of the resulting
model, both supply air and chilled water flow rate for comfortable
indoor conditions must be calculated first. This is done by analyzing
and computing the cooling loads based on the outdoor conditions.
First, it is assumed that the outdoor temperature and humidity
ratio are 33 ◦C and 0.01909 Kilogram moisture per Kilogram dry
air, respectively. Under these conditions, the HVAC inputs are cal-
culated and fed to the model of the open loop system. These inputs
were: (1) chilled water supplied to the pre-cooling coil, 0.62 kg/s,
(2) chilled water fed to the main cooling coil, 0.87 kg/s, and (3) the
sum of return air and fresh air as the total supplied air to the system,
607 L/s.
When feeding the model with the above inputs, the indoor con-
ditions which are the output of the system are observed to settle
within the comfort zone in a finite time. The results are illustrated
in Figs. 11 and 12 where the temperature and humidity ratio are
shown in Fig. 11 while Fig. 12 shows the temperature and relative
humidity. To further understand the behavior of the system, the
psychrometric chart is used in the next section.
4.2. Psychrometric process line analyses
To illustrate and validate that the system does indeed have
a big thermal inertia as initially suggested; the psychrometric
process line analyses are used. Many HVAC processes can be rep-
resented as straight lines connecting two or three state points on
the psychrometric chart. These points show the thermodynamic
properties of moist air [30,31]. Fig. 13 shows a transient state
process of conditioned space as in Section 4.1. The dotted line
represents an ideal process of these states, while the real system
takes a different path represented by the continuous line connect-
ing state (1) to state (2). This case is related to the transients of
the states. The difference between the two cases is an evidence
that the system has a thermal inertia. The difference is increased
by increasing the thermal capacitance (big thermal inertia) of the
model.
Fig. 14. Complete HVAC cycle and transient model response.](https://image.slidesharecdn.com/doublecoolingcoilmodelfornon-linearhvacsystemusingrlfmethodauthorspersonalcopy-170910133959/85/Double-cooling-coil-model-for-non-linear-hvac-system-using-rlf-method-author-s-personal-copy-12-320.jpg)
![Author's personal copy
Journal Identification = ENB Article Identification = 3159 Date: July 19, 2011 Time: 7:28 pm
2054 R.Z. Homod et al. / Energy and Buildings 43 (2011) 2043–2054
From Fig. 13, it is obvious that the final state condition (point 2)
is located inside comfort zone as expected where the comfort zone
is defined in [32].
4.3. Model validation
To validate the derived models, two different calculation meth-
ods were carried out using the indoor model conditions. At first,
comparison is done between building simulation output and calcu-
lation results by numerical methods. The data results show partial
agreement as Figs. 9 and 10. The overall system is then tested using
the psychrometric chart, showing transient response periods. Here,
the system is compared to the calculated results of every subsys-
tem process by CLF/CLTDc (cooling load factor for glass/corrected
cooling load temperature difference) method [33].
The steady state psychrometric processes’ result for each sub-
system are presented on the psychrometric chart of Fig. 14 where
it is show that the two paths ended at the same point which means
that they are related together. Process lines are colored in red to dif-
ferentiate them with the indoor transient response colored in blue.
The process started at an initial room condition (point 1) before
ending at a steady state point (point 2). The psychrometric process
lines for moisture air behavior through the subsystem model are:
1–2 moist air process line through the pre-cooling coil, 2–3 moist
air process line through the air mixing chamber, 3–4 moist air pro-
cess line through main cooling coil and 4–5 moist air process line for
building cooling load. In the figure, points 5 and 2 are almost coin-
ciding, verifying that both model behavior and CLF/CLTDc (manual
cooling load calculation) are completely correlative against each
other.
5. Conclusion
This work adopted a hybrid method that uses both physical
and empirical modeling schemes to arrive at a model that can
accurately represent a building and HVAC system with its vari-
ous thermal inertia subsystems. It was shown in the paper that
the resulting hybrid model behaved in a similar fashion to the real
system. The system does not contain different subsystems with dif-
ferent thermal inertia only, but many of its parts have pure lag
times, and they also have non-linear characteristics. In addition,
thermal load for such a system is very complex due to the chaotic
or unpredictable behaviors of many of the external and internal
disturbances to the system. One of the major unpredicted distur-
bances to the system is the variation of solar radiation, which is
very hard to model correctly. For these reasons, empirical analyses
were employed on those parts of the system. As for the HVAC equip-
ments, physical laws could be used and then linearized. The overall
model gives two coupled outputs: temperature and humidity ratio.
The obtained temperature model equation is from the ninth order
while the humidity model equation was from the eighth order. This
model with its large number of measurable variables can then be
controlled to achieve good transient and steady state responses. It
is not in the scope of this paper to perform the control design, but
it is definitely the next step of this research.
Appendix A. Supplementary data
Supplementary data associated with this article can be found, in
the online version, at doi:10.1016/j.enbuild.2011.03.023.
References
[1] D.G. Stephenson, G.P. Mitalas, Cooling load calculations by thermal response
factor method, ASHRAE Transactions 73 (1) (1967) 508–515.
[2] T. Kusuda, NBSLD: The Computer Program for Heating and Cooling Loads in
Buildings, NBS Building Science Series No. 69, National Bureau of Standards,
Washington, USA, 1976.
[3] J.A. Clarke, Environmental systems performance, Ph.D. Thesis, University of
Strathclyde, Glasgow, UK, 1977.
[4] J. Lebrun (Ed.), Proc. Int. Conf. on System Simulation in Buildings, Commission
of the European Communities, Liége, Belgium, 1982.
[5] S.O. Jensen (Ed.), Validation of Building Energy Simulation Programs. Part I and
II. Research Report PASSYS Subgroup Model Validation and Development, CEC,
Brussels, 1993, EUR 15115 EN.
[6] R. Judkoff, J. Neymark, International Energy Agency Building Energy Simulation
Test (BESTEST) and Diagnostic Method, IEA Energy Conservation in Buildings
and Community Systems Programme Annex 21 Subtask C and IEA Solar Heating
and Cooling Programme Task 12 Subtask B, 1995.
[7] ASHRAE, Standard Method of Test for the Evaluation of Building Energy Analysis
Computer Programs, ASHRAE Standard 140P, Working Draft 98/2, American
Society of Heating, Refrigerating, and Air-Conditioning Engineers, Atlanta, USA,
1998.
[8] J.A. Orosa, A new modelling methodology to control HVAC systems, Expert
Systems with Applications, in press.
[9] L.M. Viljanan Xiaosh, Controlling building indoor temperature and reducing
heating cost through night heating electric stove, Energy and Building 33 (2001)
865–873.
[10] L.M. Viljanan Xiaosh, Modeling of heat and moisture transfer in buildings,
Energy and Building 34 (2002) 1045–1054.
[11] S. Ogonowski, Modeling of the heating system in small building for control,
Energy and Buildings (March) (2010).
[12] E. Frank Kreith, Air-conditioning and refrigeration, in: Mechanical Engineering
Handbook, CRC Press LLC, Florida, 1999.
[13] N. Mendes, G.H.C. Oliveira, H.X. Araújo, L.S. Coelho, A Matlab-based simulation
tool for building thermal performance analysis, in: Eighth International IBPSA
Conference, Eindhoven, Netherlands, 2003.
[14] C.S. Barnaby, J.D. Spitler, D. Xiao, Updating the ASHRAE/ACCA residential heat-
ing and cooling load calculation procedures and data (RP-1199), in: ASHRAE
Research Project, 2004.
[15] C.S. Barnaby, J.D. Spitler, D. Xiao, The residential heat balance method for
heating and cooling load calculations (RP-1199), ASHRAE Transactions 111 (1)
(2005) 308–319.
[16] ASHRAE, Residential cooling and heating load calculations, handbook—
fundamentals, chp. 17, in: J. Clerk Maxwell (Ed.), American Society of Heat-
ing, Refrigerating, and Air-Conditioning Engineers, A Treatise on Electricity and
Magnetism, vol. 2, 3rd ed., Clarendon, Oxford, 2009[1892], pp. 68–73.
[17] R.W. Haines, Control for low humidity, Heating Piping and Air Conditioning
(August) (1980) 88–89.
[18] B. Tashtoush, M. Molhim, M. Al-Rousan, Dynamic model of an HVAC system for
control analysis, Energy 30 (10) (2005) 1729–1745.
[19] J. Wang, Z. Chunfa, J. Youyin, Hybrid CMAC-PID controller in heating ventilating
and air-conditioning system, in: IEEE International Conference on Mechatron-
ics and Automation, August 5–8, 2007, pp. 3706–3711.
[20] C. Ghiaus, A. Chicinas, C. Inard, Grey-box identification of air-handling unit
elements, Control engineering Practice (15) (2007) 421–433.
[21] Y. Wang, W.-J. Cai, Y.-C. Soh, S.-J. Li, L. Lu, L. Xie, A simplified modeling of cooling
coils for control and optimization of HVAC systems, Energy Conversion and
Management 45 (18–19) (2004) 2915–2930.
[22] T.W. Fraser Russell, A.S. Robinson, N.J. Wagner, Mass and Heat Transfer, Cam-
bridge University Press, New York, 2008.
[23] J. Stephen Blundell, M. Katherine Blundell, Concepts in Thermal Physics, Oxford
University Press, Inc., New York, 2006.
[24] C.P. Underwood, HVAC Control System: Modeling Analysis and Design, E&FN
SPON, London, 1999, p. 337.
[25] F.S. Wang, Mathematical modeling and computer simulation of insula-
tion systems in below grade applications, in: ASHRAE/DOE Conference on
Thermal Performance of the Exterior Envelopes of Buildings, Orlando, FL,
1979.
[26] T.P. Bligh, P. Shipp, G. Meixel, Energy comparisons and where to insulate earth
sheltered buildings and basements, Earth covered settlements, U.S. Depart-
ment of Energy Conference, Fort Worth, TX, 1978, K. Elissa, Title of paper if
known, unpublished.
[27] ASHRAE, HVAC Systems and Equipment’ Handbook—Fundamentals, Ameri-
can Society of Heating, Refrigerating, and Air-Conditioning Engineers, 2008
(Chp. 6).
[28] C. Ghiaus, I. Hazyuk, Calculation of optimal thermal load of interminantely
heated buildings, Energy and Buildings 42 (2010) 1248–1258.
[29] Cooling load calculation software available from URL: http://www.
carmelsoft.com, Accessed March 24, 2010.
[30] W. Haines Roger, Control Systems for Heating, Ventilating, and Air Condition-
ing, 6th ed., Springer Science & Business Media, Inc., New York, USA, 2006.
[31] T. Grondzik Walter, Air Conditioning System Design Manual, 2nd ed., Ashrae
Special Publications NE, Atlanta, 2008.
[32] ASHRAE, ANSI/ASHRAE standard 55-2004, in: Thermal Environmental Condi-
tions for Human Occupancy, American Society of Heating, Refrigerating and
Air-Conditioning Engineers, Inc., Atlanta, 2004.
[33] G. Pita Edward, Air Conditioning Principles and Systems, 4th ed., McGraw-Hill,
New York, 2002.](https://image.slidesharecdn.com/doublecoolingcoilmodelfornon-linearhvacsystemusingrlfmethodauthorspersonalcopy-170910133959/85/Double-cooling-coil-model-for-non-linear-hvac-system-using-rlf-method-author-s-personal-copy-13-320.jpg)