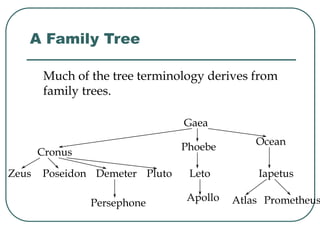
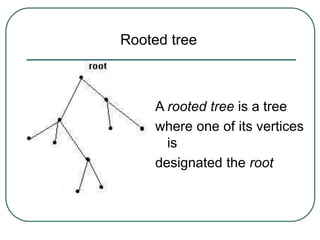
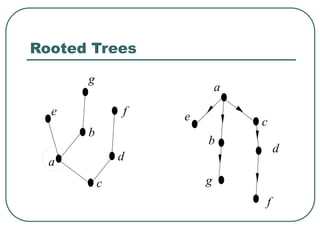
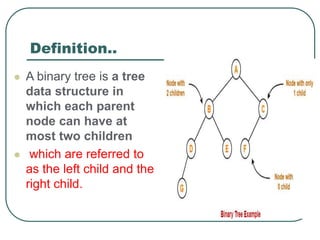
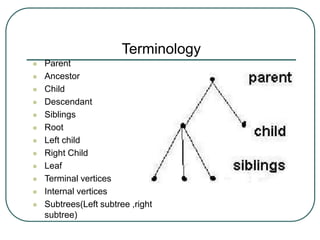
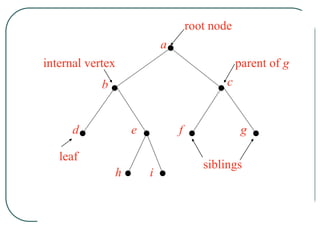
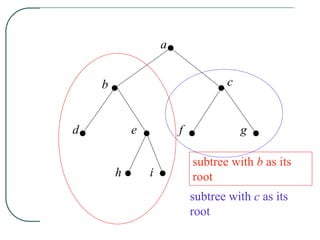
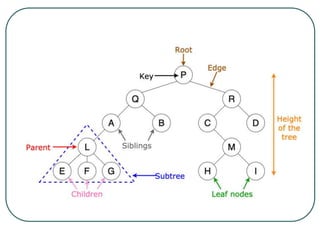
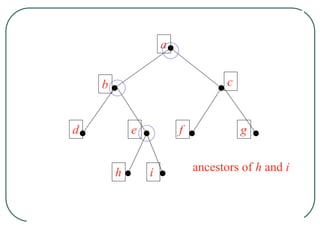
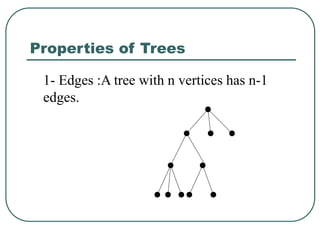
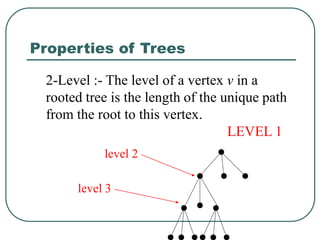
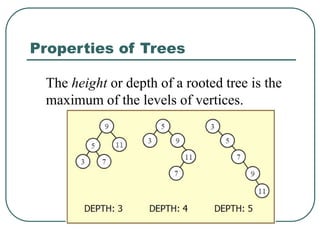
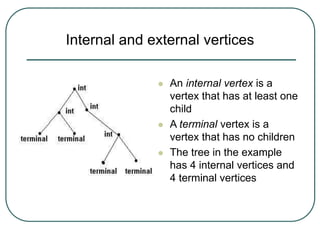
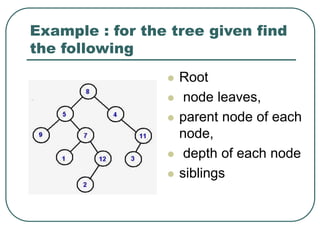
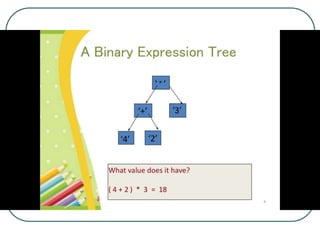
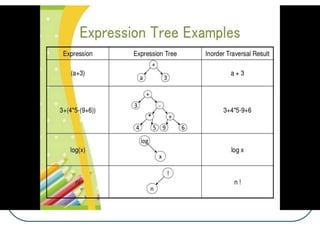
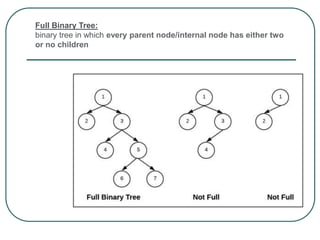
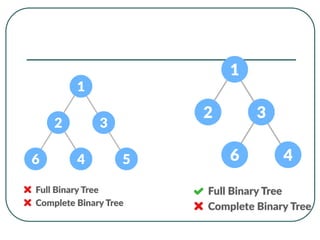
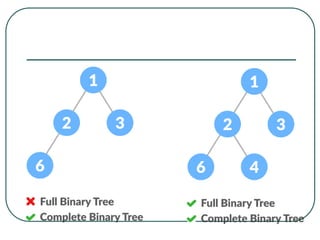
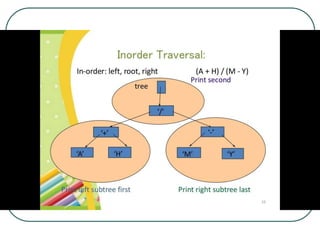
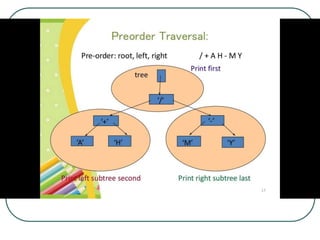
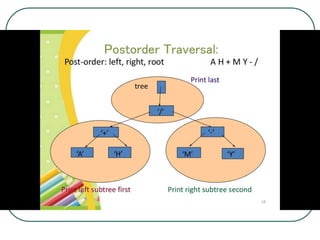
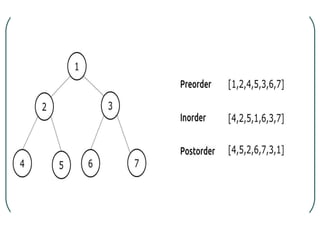
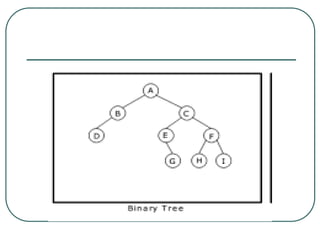
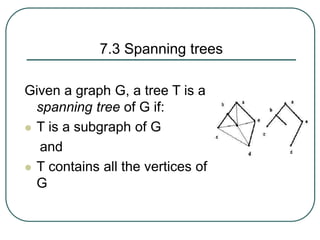
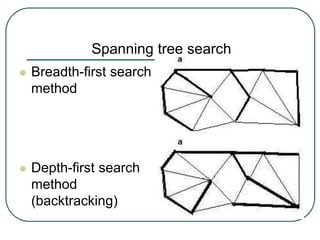
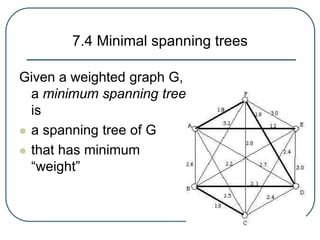
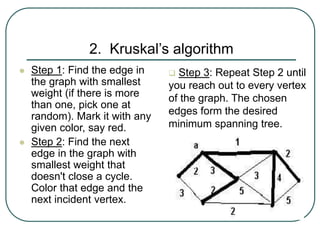
The document defines and explains key concepts related to binary trees including their terminology, properties, and different types. It discusses binary tree concepts such as parent, child, root, leaf nodes, subtrees, and full and complete binary trees. The document also covers spanning trees, minimal spanning trees, Prim's and Kruskal's algorithms for finding minimum spanning trees, and binary search trees.

1. UNIT 5
BINARY Trees

2. General Trees

3. Definition:
A tree is a connected undirected graph with
no circuits.
Recall: A circuit is a path that begins and
ends a the same vertex.

5. d
d

6. A Family Tree
Much of the tree terminology derives from
family trees.
Gaea
Cronus
Phoebe
Ocean
Zeus Poseidon Demeter Pluto Leto Iapetus
Persephone
Apollo Atlas Prometheus

7. Rooted tree
A rooted tree is a tree
where one of its vertices
is
designated the root

8. Rooted Trees
a
b
c
d
e f
g
a
b
c
d
e
f
g

9. Ordered Rooted Tree
An ordered rooted tree is a rooted tree
where the children of each internal vertex
are ordered.
If in a tree at each level , an ordering is
defined, such a tree is called an ordered
tree.

11. Definition..
 A binary tree is a tree
data structure in
which each parent
node can have at
most two children
 which are referred to
as the left child and the
right child.

12. Terminology
 Parent
 Ancestor
 Child
 Descendant
 Siblings
 Root
 Left child
 Right Child
 Leaf
 Terminal vertices
 Internal vertices
 Subtrees(Left subtree ,right
subtree)

13. root node
a
b c
d e f g
h i
parent of g
siblings
leaf
internal vertex

14. a
b c
d e f g
h i
subtree with b as its
root
subtree with c as its
root

16. a
b c
d e f g
h i ancestors of h and i

17. Properties of Trees
1- Edges :A tree with n vertices has n-1
edges.

18. Properties of Trees
2-Level :- The level of a vertex v in a
rooted tree is the length of the unique path
from the root to this vertex.
LEVEL 1
level 2
level 3

19. Properties of Trees
The height or depth of a rooted tree is the
maximum of the levels of vertices.

20. Internal and external vertices
 An internal vertex is a
vertex that has at least one
child
 A terminal vertex is a
vertex that has no children
 The tree in the example
has 4 internal vertices and
4 terminal vertices

21. Example : for the tree given find
the following
 Root
 node leaves,
 parent node of each
node,
 depth of each node
 siblings

25. Full Binary Tree:
binary tree in which every parent node/internal node has either two
or no children

26. Complete Binary Tree -
A complete binary tree is a binary tree in which all the levels are completely filled
except possibly the lowest one, which is filled from the left.
1.All the leaf elements must lean towards the left.
2.The last leaf element might not have a right sibling
i.e. a complete binary tree doesn't have to be a full binary tree.

39. 7.3 Spanning trees
Given a graph G, a tree T is a
spanning tree of G if:
 T is a subgraph of G
and
 T contains all the vertices of
G

40. Spanning tree search
 Breadth-first search
method
 Depth-first search
method
(backtracking)

41. 7.4 Minimal spanning trees
Given a weighted graph G,
a minimum spanning tree
is
 a spanning tree of G
 that has minimum
“weight”

42. 1. Prim’s algorithm
 Step 0: Pick any vertex as a
starting vertex (call it a). T = {a}.
 Step 1: Find the edge with
smallest weight incident to a.
Add it to T Also include in T the
next vertex and call it b.
 Step 2: Find the edge of
smallest weight incident to
either a or b. Include in T that
edge and the next incident
vertex. Call that vertex c.
 Step 3: Repeat Step
2, choosing the edge
of smallest weight
that does not form a
cycle until all vertices
are in T. The resulting
subgraph T is a
minimum spanning
tree.

43. 2. Kruskal’s algorithm
 Step 1: Find the edge in
the graph with smallest
weight (if there is more
than one, pick one at
random). Mark it with any
given color, say red.
 Step 2: Find the next
edge in the graph with
smallest weight that
doesn't close a cycle.
Color that edge and the
next incident vertex.
 Step 3: Repeat Step 2 until
you reach out to every vertex
of the graph. The chosen
edges form the desired
minimum spanning tree.

44. Binary search trees
 Data are associated to
each vertex
 Order data
alphabetically, so that
for each vertex v, data
to the left of v are less
than data in v
 and data to the right of
v are greater than data
in v
 Example: "Computers
are an important
technological tool"